Order-4-5 square honeycomb
| Order-4-5 square honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbols | {4,4,5} |
| Coxeter diagrams | Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination
|
| Cells | {4,4} |
| Faces | {4} |
| Edge figure | {5} |
| Vertex figure | {4,5} 
|
| Dual | {5,4,4} |
| Coxeter group | [4,4,5] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-4-5 square honeycomb is a regular space-filling tessellation (or honeycomb) with Schläfli symbol {4,4,5}. It has five square tiling {4,4} around each edge. All vertices are ultra-ideal (existing beyond the ideal boundary) with infinitely many square tiling existing around each vertex in an order-5 square tiling vertex arrangement.
Images
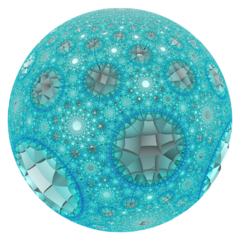 Poincaré disk model |
 Ideal surface |
Related polytopes and honeycombs
It a part of a sequence of regular polychora and honeycombs with square tiling cells: {4,4,p}
Order-4-6 square honeycomb
| Order-4-6 square honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbols | {4,4,6} {4,(4,3,4)} |
| Coxeter diagrams | Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination
|
| Cells | {4,4} |
| Faces | {4} |
| Edge figure | {6} |
| Vertex figure | {4,6} {(4,3,4)} |
| Dual | {6,4,4} |
| Coxeter group | [4,4,6] [4,((4,3,4))] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-4-6 square honeycomb is a regular space-filling tessellation (or honeycomb) with Schläfli symbol {4,4,6}. It has six square tiling, {4,4}, around each edge. All vertices are ultra-ideal (existing beyond the ideal boundary) with infinitely many square tiling existing around each vertex in an order-6 square tiling vertex arrangement.
 Poincaré disk model |
 Ideal surface |
It has a second construction as a uniform honeycomb, Schläfli symbol {4,(4,3,4)}, Coxeter diagram,
, with alternating types or colors of square tiling cells. In Coxeter notation the half symmetry is [4,4,6,1+] = [4,((4,3,4))].
Order-4-infinite square honeycomb
| Order-4-infinite square honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbols | {4,4,∞} {4,(4,∞,4)} |
| Coxeter diagrams | Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination
|
| Cells | {4,4} |
| Faces | {4} |
| Edge figure | {∞} |
| Vertex figure | {4,∞} {(4,∞,4)} |
| Dual | {∞,4,4} |
| Coxeter group | [∞,4,3] [4,((4,∞,4))] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-4-infinite square honeycomb is a regular space-filling tessellation (or honeycomb) with Schläfli symbol {4,4,∞}. It has infinitely many square tiling, {4,4}, around each edge. All vertices are ultra-ideal (existing beyond the ideal boundary) with infinitely many square tiling existing around each vertex in an infinite-order square tiling vertex arrangement.
 Poincaré disk model |
 Ideal surface |
It has a second construction as a uniform honeycomb, Schläfli symbol {4,(4,∞,4)}, Coxeter diagram,
=
, with alternating types or colors of square tiling cells. In Coxeter notation the half symmetry is [4,4,∞,1+] = [4,((4,∞,4))].
See also
- Convex uniform honeycombs in hyperbolic space
- List of regular polytopes
References
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN:0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN:0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
- Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN:0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I, II)
- George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982) [1]
- Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, (2013)[2]
- Visualizing Hyperbolic Honeycombs arXiv:1511.02851 Roice Nelson, Henry Segerman (2015)
External links
- John Baez, Visual insights: {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Plane at Infinity (2014/08/14)
- Danny Calegari, Kleinian, a tool for visualizing Kleinian groups, Geometry and the Imagination 4 March 2014. [3]
 |

