Reachability

Short description: Whether one vertex can be reached from another in a graph

In graph theory, reachability refers to the ability to get from one vertex to another within a graph. A vertex [math]\displaystyle{ s }[/math] can reach a vertex [math]\displaystyle{ t }[/math] (and [math]\displaystyle{ t }[/math] is reachable from [math]\displaystyle{ s }[/math]) if there exists a sequence of adjacent vertices (i.e. a walk) which starts with [math]\displaystyle{ s }[/math] and ends with [math]\displaystyle{ t }[/math].

In an undirected graph, reachability between all pairs of vertices can be determined by identifying the connected components of the graph. Any pair of vertices in such a graph can reach each other if and only if they belong to the same connected component; therefore, in such a graph, reachability is symmetric ([math]\displaystyle{ s }[/math] reaches [math]\displaystyle{ t }[/math] iff [math]\displaystyle{ t }[/math] reaches [math]\displaystyle{ s }[/math]). The connected components of an undirected graph can be identified in linear time. The remainder of this article focuses on the more difficult problem of determining pairwise reachability in a directed graph (which, incidentally, need not be symmetric).

Definition

For a directed graph [math]\displaystyle{ G = (V, E) }[/math], with vertex set [math]\displaystyle{ V }[/math] and edge set [math]\displaystyle{ E }[/math], the reachability relation of [math]\displaystyle{ G }[/math] is the transitive closure of [math]\displaystyle{ E }[/math], which is to say the set of all ordered pairs [math]\displaystyle{ (s,t) }[/math] of vertices in [math]\displaystyle{ V }[/math] for which there exists a sequence of vertices [math]\displaystyle{ v_0 = s, v_1, v_2, ..., v_k = t }[/math] such that the edge [math]\displaystyle{ (v_{i-1},v_i) }[/math] is in [math]\displaystyle{ E }[/math] for all [math]\displaystyle{ 1 \leq i \leq k }[/math].

If [math]\displaystyle{ G }[/math] is acyclic, then its reachability relation is a partial order; any partial order may be defined in this way, for instance as the reachability relation of its transitive reduction. A noteworthy consequence of this is that since partial orders are anti-symmetric, if [math]\displaystyle{ s }[/math] can reach [math]\displaystyle{ t }[/math], then we know that [math]\displaystyle{ t }[/math] cannot reach [math]\displaystyle{ s }[/math]. Intuitively, if we could travel from [math]\displaystyle{ s }[/math] to [math]\displaystyle{ t }[/math] and back to [math]\displaystyle{ s }[/math], then [math]\displaystyle{ G }[/math] would contain a cycle, contradicting that it is acyclic. If [math]\displaystyle{ G }[/math] is directed but not acyclic (i.e. it contains at least one cycle), then its reachability relation will correspond to a preorder instead of a partial order.

Algorithms

Algorithms for determining reachability fall into two classes: those that require preprocessing and those that do not.

If you have only one (or a few) queries to make, it may be more efficient to forgo the use of more complex data structures and compute the reachability of the desired pair directly. This can be accomplished in linear time using algorithms such as breadth first search or iterative deepening depth-first search.

If you will be making many queries, then a more sophisticated method may be used; the exact choice of method depends on the nature of the graph being analysed. In exchange for preprocessing time and some extra storage space, we can create a data structure which can then answer reachability queries on any pair of vertices in as low as [math]\displaystyle{ O(1) }[/math] time. Three different algorithms and data structures for three different, increasingly specialized situations are outlined below.

Floyd–Warshall Algorithm

The Floyd–Warshall algorithm can be used to compute the transitive closure of any directed graph, which gives rise to the reachability relation as in the definition, above.

The algorithm requires [math]\displaystyle{ O(|V|^3) }[/math] time and [math]\displaystyle{ O(|V|^2) }[/math] space in the worst case. This algorithm is not solely interested in reachability as it also computes the shortest path distance between all pairs of vertices. For graphs containing negative cycles, shortest paths may be undefined, but reachability between pairs can still be noted.

Thorup's Algorithm

For planar digraphs, a much faster method is available, as described by Mikkel Thorup in 2004. This method can answer reachability queries on a planar graph in [math]\displaystyle{ O(1) }[/math] time after spending [math]\displaystyle{ O(n \log{n}) }[/math] preprocessing time to create a data structure of [math]\displaystyle{ O(n \log{n}) }[/math] size. This algorithm can also supply approximate shortest path distances, as well as route information.

The overall approach is to associate with each vertex a relatively small set of so-called separator paths such that any path from a vertex [math]\displaystyle{ v }[/math] to any other vertex [math]\displaystyle{ w }[/math] must go through at least one of the separators associated with [math]\displaystyle{ v }[/math] or [math]\displaystyle{ w }[/math]. An outline of the reachability related sections follows.

Given a graph [math]\displaystyle{ G }[/math], the algorithm begins by organizing the vertices into layers starting from an arbitrary vertex [math]\displaystyle{ v_0 }[/math]. The layers are built in alternating steps by first considering all vertices reachable from the previous step (starting with just [math]\displaystyle{ v_0 }[/math]) and then all vertices which reach to the previous step until all vertices have been assigned to a layer. By construction of the layers, every vertex appears at most two layers, and every directed path, or dipath, in [math]\displaystyle{ G }[/math] is contained within two adjacent layers [math]\displaystyle{ L_i }[/math] and [math]\displaystyle{ L_{i+1} }[/math]. Let [math]\displaystyle{ k }[/math] be the last layer created, that is, the lowest value for [math]\displaystyle{ k }[/math] such that [math]\displaystyle{ \bigcup_{i=0}^{k} L_i = V }[/math].

The graph is then re-expressed as a series of digraphs [math]\displaystyle{ G_0, G_1, \ldots, G_{k-1} }[/math] where each [math]\displaystyle{ G_i = r_i \cup L_i \cup L_{i+1} }[/math] and where [math]\displaystyle{ r_i }[/math] is the contraction of all previous levels [math]\displaystyle{ L_0 \ldots L_{i-1} }[/math] into a single vertex. Because every dipath appears in at most two consecutive layers, and because each [math]\displaystyle{ G_i }[/math] is formed by two consecutive layers, every dipath in [math]\displaystyle{ G }[/math] appears in its entirety in at least one [math]\displaystyle{ G_i }[/math] (and no more than 2 consecutive such graphs)

For each [math]\displaystyle{ G_i }[/math], three separators are identified which, when removed, break the graph into three components which each contain at most [math]\displaystyle{ 1/2 }[/math] the vertices of the original. As [math]\displaystyle{ G_i }[/math] is built from two layers of opposed dipaths, each separator may consist of up to 2 dipaths, for a total of up to 6 dipaths over all of the separators. Let [math]\displaystyle{ S }[/math] be this set of dipaths. The proof that such separators can always be found is related to the Planar Separator Theorem of Lipton and Tarjan, and these separators can be located in linear time.

For each [math]\displaystyle{ Q \in S }[/math], the directed nature of [math]\displaystyle{ Q }[/math] provides for a natural indexing of its vertices from the start to the end of the path. For each vertex [math]\displaystyle{ v }[/math] in [math]\displaystyle{ G_i }[/math], we locate the first vertex in [math]\displaystyle{ Q }[/math] reachable by [math]\displaystyle{ v }[/math], and the last vertex in [math]\displaystyle{ Q }[/math] that reaches to [math]\displaystyle{ v }[/math]. That is, we are looking at how early into [math]\displaystyle{ Q }[/math] we can get from [math]\displaystyle{ v }[/math], and how far we can stay in [math]\displaystyle{ Q }[/math] and still get back to [math]\displaystyle{ v }[/math]. This information is stored with each [math]\displaystyle{ v }[/math]. Then for any pair of vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ w }[/math], [math]\displaystyle{ u }[/math] can reach [math]\displaystyle{ w }[/math] via [math]\displaystyle{ Q }[/math] if [math]\displaystyle{ u }[/math] connects to [math]\displaystyle{ Q }[/math] earlier than [math]\displaystyle{ w }[/math] connects from [math]\displaystyle{ Q }[/math].

Every vertex is labelled as above for each step of the recursion which builds [math]\displaystyle{ G_0 \ldots, G_k }[/math]. As this recursion has logarithmic depth, a total of [math]\displaystyle{ O(\log{n}) }[/math] extra information is stored per vertex. From this point, a logarithmic time query for reachability is as simple as looking over each pair of labels for a common, suitable [math]\displaystyle{ Q }[/math]. The original paper then works to tune the query time down to [math]\displaystyle{ O(1) }[/math].

In summarizing the analysis of this method, first consider that the layering approach partitions the vertices so that each vertex is considered only [math]\displaystyle{ O(1) }[/math] times. The separator phase of the algorithm breaks the graph into components which are at most [math]\displaystyle{ 1/2 }[/math] the size of the original graph, resulting in a logarithmic recursion depth. At each level of the recursion, only linear work is needed to identify the separators as well as the connections possible between vertices. The overall result is [math]\displaystyle{ O(n \log n) }[/math] preprocessing time with only [math]\displaystyle{ O(\log{n}) }[/math] additional information stored for each vertex.

Kameda's Algorithm

A suitable digraph for Kameda's method with [math]\displaystyle{ s }[/math] and [math]\displaystyle{ t }[/math] added.

The same graph as above after Kameda's algorithm has run, showing the DFS labels for each vertex

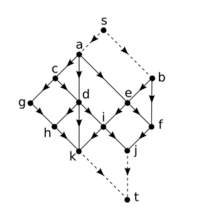
An even faster method for pre-processing, due to T. Kameda in 1975, can be used if the graph is planar, acyclic, and also exhibits the following additional properties: all 0-indegree and all 0-outdegree vertices appear on the same face (often assumed to be the outer face), and it is possible to partition the boundary of that face into two parts such that all 0-indegree vertices appear on one part, and all 0-outdegree vertices appear on the other (i.e. the two types of vertices do not alternate).

If [math]\displaystyle{ G }[/math] exhibits these properties, then we can preprocess the graph in only [math]\displaystyle{ O(n) }[/math] time, and store only [math]\displaystyle{ O(\log{n}) }[/math] extra bits per vertex, answering reachability queries for any pair of vertices in [math]\displaystyle{ O(1) }[/math] time with a simple comparison.

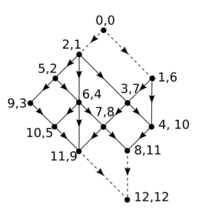
Preprocessing performs the following steps. We add a new vertex [math]\displaystyle{ s }[/math] which has an edge to each 0-indegree vertex, and another new vertex [math]\displaystyle{ t }[/math] with edges from each 0-outdegree vertex. Note that the properties of [math]\displaystyle{ G }[/math] allow us to do so while maintaining planarity, that is, there will still be no edge crossings after these additions. For each vertex we store the list of adjacencies (out-edges) in order of the planarity of the graph (for example, clockwise with respect to the graph's embedding). We then initialize a counter [math]\displaystyle{ i = n + 1 }[/math] and begin a Depth-First Traversal from [math]\displaystyle{ s }[/math]. During this traversal, the adjacency list of each vertex is visited from left-to-right as needed. As vertices are popped from the traversal's stack, they are labelled with the value [math]\displaystyle{ i }[/math], and [math]\displaystyle{ i }[/math] is then decremented. Note that [math]\displaystyle{ t }[/math] is always labelled with the value [math]\displaystyle{ n+1 }[/math] and [math]\displaystyle{ s }[/math] is always labelled with [math]\displaystyle{ 0 }[/math]. The depth-first traversal is then repeated, but this time the adjacency list of each vertex is visited from right-to-left.

When completed, [math]\displaystyle{ s }[/math] and [math]\displaystyle{ t }[/math], and their incident edges, are removed. Each remaining vertex stores a 2-dimensional label with values from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ n }[/math]. Given two vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math], and their labels [math]\displaystyle{ L(u) = (a_1, a_2) }[/math] and [math]\displaystyle{ L(v) =(b_1, b_2) }[/math], we say that [math]\displaystyle{ L(u) \lt L(v) }[/math] if and only if [math]\displaystyle{ a_1 \leq b_1 }[/math], [math]\displaystyle{ a_2 \leq b_2 }[/math], and there exists at least one component [math]\displaystyle{ a_1 }[/math] or [math]\displaystyle{ a_2 }[/math] which is strictly less than [math]\displaystyle{ b_1 }[/math] or [math]\displaystyle{ b_2 }[/math], respectively.

The main result of this method then states that [math]\displaystyle{ v }[/math] is reachable from [math]\displaystyle{ u }[/math] if and only if [math]\displaystyle{ L(u) \lt L(v) }[/math], which is easily calculated in [math]\displaystyle{ O(1) }[/math] time.

Related problems

A related problem is to solve reachability queries with some number [math]\displaystyle{ k }[/math] of vertex failures. For example: "Can vertex [math]\displaystyle{ u }[/math] still reach vertex [math]\displaystyle{ v }[/math] even though vertices [math]\displaystyle{ s_1, s_2, ..., s_k }[/math] have failed and can no longer be used?" A similar problem may consider edge failures rather than vertex failures, or a mix of the two. The breadth-first search technique works just as well on such queries, but constructing an efficient oracle is more challenging.

Another problem related to reachability queries is in quickly recalculating changes to reachability relationships when some portion of the graph is changed. For example, this is a relevant concern to garbage collection which needs to balance the reclamation of memory (so that it may be reallocated) with the performance concerns of the running application.

See also

• Gammoid
• st-connectivity