Golem (ILP)

Golem is an inductive logic programming algorithm developed by Stephen Muggleton and Cao Feng in 1990. It uses the technique of relative least general generalisation proposed by Gordon Plotkin, leading to a bottom-up search through the subsumption lattice. In 1992, shortly after its introduction, Golem was considered the only inductive logic programming system capable of scaling to tens of thousands of examples.

Description

Golem takes as input a definite program B as background knowledge together with sets of positive and negative examples, denoted [math]\displaystyle{ E^{+} }[/math] and [math]\displaystyle{ E^{-} }[/math] respectively. The overall idea is to construct the least general generalisation of [math]\displaystyle{ E^{+} }[/math] with respect to the background knowledge. However, if B is not merely a finite set of ground atoms, then this relative least general generalisation may not exist. Therefore, rather than using B directly, Golem uses the set [math]\displaystyle{ B^{h} }[/math] of all ground atoms that can be resolved from B in at most h resolution steps. An additional difficulty is that if [math]\displaystyle{ E^{-} }[/math] is non-empty, the least general generalisation of [math]\displaystyle{ E^{+} }[/math] may entail a negative example. In this case, Golem generalises different subsets of [math]\displaystyle{ E^{+} }[/math] separately to obtain a program of several clauses. Golem also employs some restrictions on the hypothesis space, ensuring that relative least general generalisations are polynomial in the number of training examples. Golem demands that all variables in the head of a clause also appears in a literal of the clause body; that the number of substitutions needed to instantiate existentially quantified variables introduced in a literal is bounded; and that the depth of the chain of substitutions needed to instantiate such a variable is also bounded.

Example

Assumed family relations

The following example about learning definitions of family relations uses the abbreviations

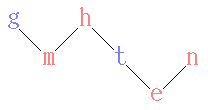
par: parent, fem: female, dau: daughter, g: George, h: Helen, m: Mary, t: Tom, n: Nancy, and e: Eve.

It starts from the background knowledge (cf. picture)

[math]\displaystyle{ \textit{par}(h,m) \land \textit{par}(h,t) \land \textit{par}(g,m) \land \textit{par}(t,e) \land \textit{par}(n,e) \land \textit{fem}(h) \land \textit{fem}(m) \land \textit{fem}(n) \land \textit{fem}(e) }[/math],

the positive examples

[math]\displaystyle{ \textit{dau}(m,h) \land \textit{dau}(e,t) }[/math],

and the trivial proposition true to denote the absence of negative examples.

The relative least general generalisation is now computed as follows to obtain a definition of the daughter relation.

• Relativise each positive example literal with the complete background knowledge:

  [math]\displaystyle{ \begin{align} \textit{dau}(m,h) \leftarrow \textit{par}(h,m) \land \textit{par}(h,t) \land \textit{par}(g,m) \land \textit{par}(t,e) \land \textit{par}(n,e) \land \textit{fem}(h) \land \textit{fem}(m) \land \textit{fem}(n) \land \textit{fem}(e) \\ \textit{dau}(e,t) \leftarrow \textit{par}(h,m) \land \textit{par}(h,t) \land \textit{par}(g,m) \land \textit{par}(t,e) \land \textit{par}(n,e) \land \textit{fem}(h) \land \textit{fem}(m) \land \textit{fem}(n) \land \textit{fem}(e) \end{align} }[/math],

• Convert into clause normal form:

  [math]\displaystyle{ \begin{align} \textit{dau}(m,h) \lor \lnot \textit{par}(h,m) \lor \lnot \textit{par}(h,t) \lor \lnot \textit{par}(g,m) \lor \lnot \textit{par}(t,e) \lor \lnot \textit{par}(n,e) \lor \lnot \textit{fem}(h) \lor \lnot \textit{fem}(m) \lor \lnot \textit{fem}(n) \lor \lnot \textit{fem}(e) \\ \textit{dau}(e,t) \lor \lnot \textit{par}(h,m) \lor \lnot \textit{par}(h,t) \lor \lnot \textit{par}(g,m) \lor \lnot \textit{par}(t,e) \lor \lnot \textit{par}(n,e) \lor \lnot \textit{fem}(h) \lor \lnot \textit{fem}(m) \lor \lnot \textit{fem}(n) \lor \lnot \textit{fem}(e) \end{align} }[/math],

• Anti-unify each compatible pair of literals:
  • [math]\displaystyle{ \textit{dau}(x_{me},x_{ht}) }[/math] from [math]\displaystyle{ \textit{dau}(m,h) }[/math] and [math]\displaystyle{ \textit{dau}(e,t) }[/math],
  • [math]\displaystyle{ \lnot \textit{par}(x_{ht},x_{me}) }[/math] from [math]\displaystyle{ \lnot \textit{par}(h,m) }[/math] and [math]\displaystyle{ \lnot \textit{par}(t,e) }[/math],
  • [math]\displaystyle{ \lnot \textit{fem}(x_{me}) }[/math] from [math]\displaystyle{ \lnot \textit{fem}(m) }[/math] and [math]\displaystyle{ \lnot \textit{fem}(e) }[/math],
  • [math]\displaystyle{ \lnot \textit{par}(g,m) }[/math] from [math]\displaystyle{ \lnot \textit{par}(g,m) }[/math] and [math]\displaystyle{ \lnot \textit{par}(g,m) }[/math], similar for all other background-knowledge literals
  • [math]\displaystyle{ \lnot \textit{par}(x_{gt},x_{me}) }[/math] from [math]\displaystyle{ \lnot \textit{par}(g,m) }[/math] and [math]\displaystyle{ \lnot \textit{par}(t,e) }[/math], and many more negated literals
• Delete all negated literals containing variables that don't occur in a positive literal:
  • after deleting all negated literals containing other variables than [math]\displaystyle{ x_{me},x_{ht} }[/math], only [math]\displaystyle{ \textit{dau}(x_{me},x_{ht}) \lor \lnot \textit{par}(x_{ht},x_{me}) \lor \lnot \textit{fem}(x_{me}) }[/math] remains, together with all ground literals from the background knowledge
• Convert clauses back to Horn form:
  • [math]\displaystyle{ \textit{dau}(x_{me},x_{ht}) \leftarrow \textit{par}(x_{ht},x_{me}) \land \textit{fem}(x_{me}) \land (\text{all background knowledge facts}) }[/math]

The resulting Horn clause is the hypothesis h obtained by Golem. Informally, the clause reads "[math]\displaystyle{ x_{me} }[/math] is called a daughter of [math]\displaystyle{ x_{ht} }[/math] if [math]\displaystyle{ x_{ht} }[/math] is the parent of [math]\displaystyle{ x_{me} }[/math] and [math]\displaystyle{ x_{me} }[/math] is female", which is a commonly accepted definition.