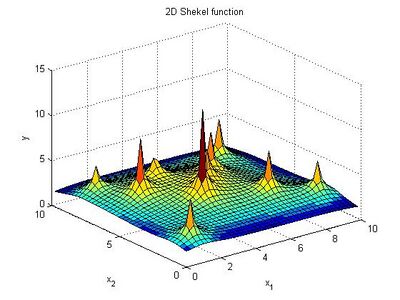
Shekel function

Short description: Function used as a performance test problem for optimization algorithms

A Shekel function in 2 dimensions and with 10 maxima

The Shekel function or also Shekel's foxholes is a multidimensional, multimodal, continuous, deterministic function commonly used as a test function for testing optimization techniques.

The mathematical form of a function in [math]\displaystyle{ n }[/math] dimensions with [math]\displaystyle{ m }[/math] maxima is:

[math]\displaystyle{ f(\vec{x}) = \sum_{i = 1}^{m} \; \left( c_{i} + \sum\limits_{j = 1}^{n} (x_{j} - a_{ji})^2 \right)^{-1} }[/math]

or, similarly,

[math]\displaystyle{ f(x_1,x_2,...,x_{n-1},x_n) = \sum_{i = 1}^{m} \; \left( c_{i} + \sum\limits_{j = 1}^{n} (x_{j} - a_{ij})^2 \right)^{-1} }[/math]

Global minima

Numerically certified global minima and the corresponding solutions were obtained using interval methods for up to [math]\displaystyle{ n = 10 }[/math].

See also

• Test functions for optimization

Further reading

Shekel, J. 1971. "Test Functions for Multimodal Search Techniques." Fifth Annual Princeton Conference on Information Science and Systems.