Table of spherical harmonics

Short description: Mathematical table

This is a table of orthonormalized spherical harmonics that employ the Condon-Shortley phase up to degree [math]\displaystyle{ \ell = 10 }[/math]. Some of these formulas are expressed in terms of the Cartesian expansion of the spherical harmonics into polynomials in x, y, z, and r. For purposes of this table, it is useful to express the usual spherical to Cartesian transformations that relate these Cartesian components to [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \varphi }[/math] as

[math]\displaystyle{ \begin{cases} \cos(\theta) & = z/r\\ e^{\pm i\varphi} \cdot \sin(\theta) & = (x \pm iy)/r \end{cases} }[/math]

Complex spherical harmonics

For ℓ = 0, …, 5, see.

ℓ = 0

[math]\displaystyle{ Y_{0}^{0}(\theta,\varphi)={1\over 2}\sqrt{1\over \pi} }[/math]

ℓ = 1

[math]\displaystyle{ \begin{align} Y_{1}^{-1}(\theta,\varphi) &= & & {1\over 2}\sqrt{3\over 2\pi}\cdot e^{-i\varphi}\cdot\sin\theta & &= & &{1\over 2}\sqrt{3\over 2\pi} \cdot{(x-iy)\over r} \\ Y_{1}^{ 0}(\theta,\varphi) &= & & {1\over 2}\sqrt{3\over \pi}\cdot \cos\theta & &= & &{1\over 2}\sqrt{3\over \pi} \cdot{z\over r} \\ Y_{1}^{ 1}(\theta,\varphi) &= &-& {1\over 2}\sqrt{3\over 2\pi}\cdot e^{i\varphi}\cdot \sin\theta & &= &-&{1\over 2}\sqrt{3\over 2\pi} \cdot{(x+iy)\over r} \end{align} }[/math]

ℓ = 2

[math]\displaystyle{ \begin{align} Y_{2}^{-2}(\theta,\varphi)&=& &{1\over 4}\sqrt{15\over 2\pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\quad &&=& &{1\over 4}\sqrt{15\over 2\pi}\cdot{(x - iy)^2 \over r^{2}}&\\ Y_{2}^{-1}(\theta,\varphi)&=& &{1\over 2}\sqrt{15\over 2\pi}\cdot e^{-i\varphi}\cdot\sin \theta\cdot \cos\theta\quad &&=& &{1\over 2}\sqrt{15\over 2\pi}\cdot{(x - iy) \cdot z \over r^{2}}&\\ Y_{2}^{ 0}(\theta,\varphi)&=& &{1\over 4}\sqrt{ 5\over \pi}\cdot (3\cos^{2}\theta-1)\quad&&=& &{1\over 4}\sqrt{ 5\over \pi}\cdot{(3z^{2}-r^{2})\over r^{2}}&\\ Y_{2}^{ 1}(\theta,\varphi)&=&-&{1\over 2}\sqrt{15\over 2\pi}\cdot e^{ i\varphi}\cdot\sin \theta\cdot \cos\theta\quad &&=&-&{1\over 2}\sqrt{15\over 2\pi}\cdot{(x + iy) \cdot z \over r^{2}}&\\ Y_{2}^{ 2}(\theta,\varphi)&=& &{1\over 4}\sqrt{15\over 2\pi}\cdot e^{ 2i\varphi}\cdot\sin^{2}\theta\quad &&=& &{1\over 4}\sqrt{15\over 2\pi}\cdot{(x + iy)^2 \over r^{2}}& \end{align} }[/math]

ℓ = 3

[math]\displaystyle{ \begin{align} Y_{3}^{-3}(\theta,\varphi) &=& &{1\over 8}\sqrt{ 35\over \pi}\cdot e^{-3i\varphi}\cdot\sin^{3}\theta\quad& &=& & {1\over 8}\sqrt{35\over \pi}\cdot{(x - iy)^{3}\over r^{3}}&\\ Y_{3}^{-2}(\theta,\varphi) &=& &{1\over 4}\sqrt{105\over 2\pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\cdot\cos\theta\quad& &=& & {1\over 4}\sqrt{105\over 2\pi}\cdot{(x- iy)^2 \cdot z \over r^{3}}&\\ Y_{3}^{-1}(\theta,\varphi) &=& &{1\over 8}\sqrt{ 21\over \pi}\cdot e^{-i\varphi}\cdot\sin\theta\cdot(5\cos^{2}\theta-1)\quad& &=& &{1\over 8}\sqrt{21\over \pi}\cdot{(x - iy) \cdot (5z^2- r^2)\over r^{3}}&\\ Y_{3}^{ 0}(\theta,\varphi) &=& &{1\over 4}\sqrt{ 7\over \pi}\cdot(5\cos^{3}\theta-3\cos\theta)\quad& &=& &{1\over 4}\sqrt{7\over \pi}\cdot{(5z^3 - 3zr^2)\over r^{3}}&\\ Y_{3}^{ 1}(\theta,\varphi) &=&-&{1\over 8}\sqrt{ 21\over \pi}\cdot e^ { i\varphi}\cdot\sin\theta\cdot(5\cos^{2}\theta-1)\quad& &=& &{-1\over 8}\sqrt{21\over \pi}\cdot{(x + iy) \cdot (5z^2 - r^2) \over r^{3}}&\\ Y_{3}^{ 2}(\theta,\varphi) &=& &{1\over 4}\sqrt{105\over 2\pi}\cdot e^ {2i\varphi}\cdot\sin^{2}\theta\cdot\cos\theta\quad& &=& &{1\over 4}\sqrt{105\over 2\pi}\cdot{(x + iy)^2 \cdot z \over r^{3}}&\\ Y_{3}^{ 3}(\theta,\varphi) &=&-&{1\over 8}\sqrt{ 35\over \pi}\cdot e^ {3i\varphi}\cdot\sin^{3}\theta\quad& &=& &{-1\over 8}\sqrt{35\over \pi}\cdot{(x + iy)^3\over r^{3}}& \end{align} }[/math]

ℓ = 4

[math]\displaystyle{ \begin{align} Y_{4}^{-4}(\theta,\varphi)&={ 3\over 16}\sqrt{35\over 2\pi}\cdot e^{-4i\varphi}\cdot\sin^{4}\theta= \frac{3}{16} \sqrt{\frac{35}{2 \pi}} \cdot \frac{(x - i y)^4}{r^4}\\ Y_{4}^{-3}(\theta,\varphi)&={ 3\over 8}\sqrt{35\over \pi}\cdot e^{-3i\varphi}\cdot\sin^{3}\theta\cdot\cos\theta= \frac{3}{8} \sqrt{\frac{35}{\pi}} \cdot \frac{(x - i y)^3 z}{r^4}\\ Y_{4}^{-2}(\theta,\varphi)&={ 3\over 8}\sqrt{ 5\over 2\pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\cdot(7\cos^{2}\theta-1)= \frac{3}{8} \sqrt{\frac{5}{2 \pi}} \cdot \frac{(x - i y)^2 \cdot (7 z^2 - r^2)}{r^4}\\ Y_{4}^{-1}(\theta,\varphi)&={ 3\over 8}\sqrt{ 5\over \pi}\cdot e^{- i\varphi}\cdot\sin\theta\cdot(7\cos^{3}\theta-3\cos\theta)= \frac{3}{8} \sqrt{\frac{5}{\pi}} \cdot \frac{(x - i y) \cdot (7 z^3 - 3 z r^2)}{r^4}\\ Y_{4}^{ 0}(\theta,\varphi)&={ 3\over 16}\sqrt{ 1\over \pi}\cdot(35\cos^{4}\theta-30\cos^{2}\theta+3)= \frac{3}{16} \sqrt{\frac{1}{\pi}} \cdot \frac{(35 z^4 - 30 z^2 r^2 + 3 r^4)}{r^4}\\ Y_{4}^{ 1}(\theta,\varphi)&={-3\over 8}\sqrt{ 5\over \pi}\cdot e^{ i\varphi}\cdot\sin\theta\cdot(7\cos^{3}\theta-3\cos\theta)= \frac{- 3}{8} \sqrt{\frac{5}{\pi}} \cdot \frac{(x + i y) \cdot (7 z^3 - 3 z r^2)}{r^4}\\ Y_{4}^{ 2}(\theta,\varphi)&={ 3\over 8}\sqrt{ 5\over 2\pi}\cdot e^{ 2i\varphi}\cdot\sin^{2}\theta\cdot(7\cos^{2}\theta-1)= \frac{3}{8} \sqrt{\frac{5}{2 \pi}} \cdot \frac{(x + i y)^2 \cdot (7 z^2 - r^2)}{r^4}\\ Y_{4}^{ 3}(\theta,\varphi)&={-3\over 8}\sqrt{35\over \pi}\cdot e^{ 3i\varphi}\cdot\sin^{3}\theta\cdot\cos\theta= \frac{- 3}{8} \sqrt{\frac{35}{\pi}} \cdot \frac{(x + i y)^3 z}{r^4}\\ Y_{4}^{ 4}(\theta,\varphi)&={ 3\over 16}\sqrt{35\over 2\pi}\cdot e^{ 4i\varphi}\cdot\sin^{4}\theta= \frac{3}{16} \sqrt{\frac{35}{2 \pi}} \cdot \frac{(x + i y)^4}{r^4} \end{align} }[/math]

ℓ = 5

[math]\displaystyle{ \begin{align} Y_{5}^{-5}(\theta,\varphi)&={ 3\over 32}\sqrt{ 77\over \pi}\cdot e^{-5i\varphi}\cdot\sin^{5}\theta\\ Y_{5}^{-4}(\theta,\varphi)&={ 3\over 16}\sqrt{ 385\over 2\pi}\cdot e^{-4i\varphi}\cdot\sin^{4}\theta\cdot\cos\theta\\ Y_{5}^{-3}(\theta,\varphi)&={ 1\over 32}\sqrt{ 385\over \pi}\cdot e^{-3i\varphi}\cdot\sin^{3}\theta\cdot(9\cos^{2}\theta-1)\\ Y_{5}^{-2}(\theta,\varphi)&={ 1\over 8}\sqrt{1155\over 2\pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\cdot(3\cos^{3}\theta-\cos\theta)\\ Y_{5}^{-1}(\theta,\varphi)&={ 1\over 16}\sqrt{ 165\over 2\pi}\cdot e^{- i\varphi}\cdot\sin \theta\cdot(21\cos^{4}\theta-14\cos^{2}\theta+1)\\ Y_{5}^{ 0}(\theta,\varphi)&={ 1\over 16}\sqrt{ 11\over \pi}\cdot (63\cos^{5}\theta-70\cos^{3}\theta+15\cos\theta)\\ Y_{5}^{ 1}(\theta,\varphi)&={-1\over 16}\sqrt{ 165\over 2\pi}\cdot e^{ i\varphi}\cdot\sin \theta\cdot(21\cos^{4}\theta-14\cos^{2}\theta+1)\\ Y_{5}^{ 2}(\theta,\varphi)&={ 1\over 8}\sqrt{1155\over 2\pi}\cdot e^{ 2i\varphi}\cdot\sin^{2}\theta\cdot(3\cos^{3}\theta-\cos\theta)\\ Y_{5}^{ 3}(\theta,\varphi)&={-1\over 32}\sqrt{ 385\over \pi}\cdot e^{ 3i\varphi}\cdot\sin^{3}\theta\cdot(9\cos^{2}\theta-1)\\ Y_{5}^{ 4}(\theta,\varphi)&={ 3\over 16}\sqrt{ 385\over 2\pi}\cdot e^{ 4i\varphi}\cdot\sin^{4}\theta\cdot\cos\theta\\ Y_{5}^{ 5}(\theta,\varphi)&={-3\over 32}\sqrt{ 77\over \pi}\cdot e^{ 5i\varphi}\cdot\sin^{5}\theta \end{align} }[/math]

ℓ = 6

[math]\displaystyle{ \begin{align} Y_{6}^{-6}(\theta,\varphi)&= {1\over 64}\sqrt{3003\over \pi}\cdot e^{-6i\varphi}\cdot\sin^{6}\theta\\ Y_{6}^{-5}(\theta,\varphi)&= {3\over 32}\sqrt{1001\over \pi}\cdot e^{-5i\varphi}\cdot\sin^{5}\theta\cdot\cos\theta\\ Y_{6}^{-4}(\theta,\varphi)&= {3\over 32}\sqrt{ 91\over 2\pi}\cdot e^{-4i\varphi}\cdot\sin^{4}\theta\cdot(11\cos^{2}\theta-1)\\ Y_{6}^{-3}(\theta,\varphi)&= {1\over 32}\sqrt{1365\over \pi}\cdot e^{-3i\varphi}\cdot\sin^{3}\theta\cdot(11\cos^{3}\theta-3\cos\theta)\\ Y_{6}^{-2}(\theta,\varphi)&= {1\over 64}\sqrt{1365\over \pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\cdot(33\cos^{4}\theta-18\cos^{2}\theta+1)\\ Y_{6}^{-1}(\theta,\varphi)&= {1\over 16}\sqrt{ 273\over 2\pi}\cdot e^{- i\varphi}\cdot\sin \theta\cdot(33\cos^{5}\theta-30\cos^{3}\theta+5\cos\theta)\\ Y_{6}^{ 0}(\theta,\varphi)&= {1\over 32}\sqrt{ 13\over \pi}\cdot (231\cos^{6}\theta-315\cos^{4}\theta+105\cos^{2}\theta-5)\\ Y_{6}^{ 1}(\theta,\varphi)&=-{1\over 16}\sqrt{ 273\over 2\pi}\cdot e^{ i\varphi}\cdot\sin \theta\cdot(33\cos^{5}\theta-30\cos^{3}\theta+5\cos\theta)\\ Y_{6}^{ 2}(\theta,\varphi)&= {1\over 64}\sqrt{1365\over \pi}\cdot e^{ 2i\varphi}\cdot\sin^{2}\theta\cdot(33\cos^{4}\theta-18\cos^{2}\theta+1)\\ Y_{6}^{ 3}(\theta,\varphi)&=-{1\over 32}\sqrt{1365\over \pi}\cdot e^{ 3i\varphi}\cdot\sin^{3}\theta\cdot(11\cos^{3}\theta-3\cos\theta)\\ Y_{6}^{ 4}(\theta,\varphi)&= {3\over 32}\sqrt{ 91\over 2\pi}\cdot e^{ 4i\varphi}\cdot\sin^{4}\theta\cdot(11\cos^{2}\theta-1)\\ Y_{6}^{ 5}(\theta,\varphi)&=-{3\over 32}\sqrt{1001\over \pi}\cdot e^{ 5i\varphi}\cdot\sin^{5}\theta\cdot\cos\theta\\ Y_{6}^{ 6}(\theta,\varphi)&= {1\over 64}\sqrt{3003\over \pi}\cdot e^{ 6i\varphi}\cdot\sin^{6}\theta \end{align} }[/math]

ℓ = 7

[math]\displaystyle{ \begin{align} Y_{7}^{-7}(\theta,\varphi)&= {3\over 64}\sqrt{ 715\over 2\pi}\cdot e^{-7i\varphi}\cdot\sin^{7}\theta\\ Y_{7}^{-6}(\theta,\varphi)&= {3\over 64}\sqrt{5005\over \pi}\cdot e^{-6i\varphi}\cdot\sin^{6}\theta\cdot\cos\theta\\ Y_{7}^{-5}(\theta,\varphi)&= {3\over 64}\sqrt{ 385\over 2\pi}\cdot e^{-5i\varphi}\cdot\sin^{5}\theta\cdot(13\cos^{2}\theta-1)\\ Y_{7}^{-4}(\theta,\varphi)&= {3\over 32}\sqrt{ 385\over 2\pi}\cdot e^{-4i\varphi}\cdot\sin^{4}\theta\cdot(13\cos^{3}\theta-3\cos\theta)\\ Y_{7}^{-3}(\theta,\varphi)&= {3\over 64}\sqrt{ 35\over 2\pi}\cdot e^{-3i\varphi}\cdot\sin^{3}\theta\cdot(143\cos^{4}\theta-66\cos^{2}\theta+3)\\ Y_{7}^{-2}(\theta,\varphi)&= {3\over 64}\sqrt{ 35\over \pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\cdot(143\cos^{5}\theta-110\cos^{3}\theta+15\cos\theta)\\ Y_{7}^{-1}(\theta,\varphi)&= {1\over 64}\sqrt{ 105\over 2\pi}\cdot e^{- i\varphi}\cdot\sin \theta\cdot(429\cos^{6}\theta-495\cos^{4}\theta+135\cos^{2}\theta-5)\\ Y_{7}^{ 0}(\theta,\varphi)&= {1\over 32}\sqrt{ 15\over \pi}\cdot (429\cos^{7}\theta-693\cos^{5}\theta+315\cos^{3}\theta-35\cos\theta)\\ Y_{7}^{ 1}(\theta,\varphi)&=-{1\over 64}\sqrt{ 105\over 2\pi}\cdot e^{ i\varphi}\cdot\sin \theta\cdot(429\cos^{6}\theta-495\cos^{4}\theta+135\cos^{2}\theta-5)\\ Y_{7}^{ 2}(\theta,\varphi)&= {3\over 64}\sqrt{ 35\over \pi}\cdot e^{ 2i\varphi}\cdot\sin^{2}\theta\cdot(143\cos^{5}\theta-110\cos^{3}\theta+15\cos\theta)\\ Y_{7}^{ 3}(\theta,\varphi)&=-{3\over 64}\sqrt{ 35\over 2\pi}\cdot e^{ 3i\varphi}\cdot\sin^{3}\theta\cdot(143\cos^{4}\theta-66\cos^{2}\theta+3)\\ Y_{7}^{ 4}(\theta,\varphi)&= {3\over 32}\sqrt{ 385\over 2\pi}\cdot e^{ 4i\varphi}\cdot\sin^{4}\theta\cdot(13\cos^{3}\theta-3\cos\theta)\\ Y_{7}^{ 5}(\theta,\varphi)&=-{3\over 64}\sqrt{ 385\over 2\pi}\cdot e^{ 5i\varphi}\cdot\sin^{5}\theta\cdot(13\cos^{2}\theta-1)\\ Y_{7}^{ 6}(\theta,\varphi)&= {3\over 64}\sqrt{5005\over \pi}\cdot e^{ 6i\varphi}\cdot\sin^{6}\theta\cdot\cos\theta\\ Y_{7}^{ 7}(\theta,\varphi)&=-{3\over 64}\sqrt{ 715\over 2\pi}\cdot e^{ 7i\varphi}\cdot\sin^{7}\theta \end{align} }[/math]

ℓ = 8

[math]\displaystyle{ \begin{align} Y_{8}^{-8}(\theta,\varphi)&={ 3\over 256}\sqrt{12155\over 2\pi}\cdot e^{-8i\varphi}\cdot\sin^{8}\theta\\ Y_{8}^{-7}(\theta,\varphi)&={ 3\over 64}\sqrt{12155\over 2\pi}\cdot e^{-7i\varphi}\cdot\sin^{7}\theta\cdot\cos\theta\\ Y_{8}^{-6}(\theta,\varphi)&={ 1\over 128}\sqrt{7293\over \pi}\cdot e^{-6i\varphi}\cdot\sin^{6}\theta\cdot(15\cos^{2}\theta-1)\\ Y_{8}^{-5}(\theta,\varphi)&={ 3\over 64}\sqrt{17017\over 2\pi}\cdot e^{-5i\varphi}\cdot\sin^{5}\theta\cdot(5\cos^{3}\theta-\cos\theta)\\ Y_{8}^{-4}(\theta,\varphi)&={ 3\over 128}\sqrt{1309\over 2\pi}\cdot e^{-4i\varphi}\cdot\sin^{4}\theta\cdot(65\cos^{4}\theta-26\cos^{2}\theta+1)\\ Y_{8}^{-3}(\theta,\varphi)&={ 1\over 64}\sqrt{19635\over 2\pi}\cdot e^{-3i\varphi}\cdot\sin^{3}\theta\cdot(39\cos^{5}\theta-26\cos^{3}\theta+3\cos\theta)\\ Y_{8}^{-2}(\theta,\varphi)&={ 3\over 128}\sqrt{595\over \pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\cdot(143\cos^{6}\theta-143\cos^{4}\theta+33\cos^{2}\theta-1)\\ Y_{8}^{-1}(\theta,\varphi)&={ 3\over 64}\sqrt{17\over 2\pi}\cdot e^{-i\varphi}\cdot\sin\theta\cdot(715\cos^{7}\theta-1001\cos^{5}\theta+385\cos^{3}\theta-35\cos\theta)\\ Y_{8}^{ 0}(\theta,\varphi)&={ 1\over 256}\sqrt{17\over \pi}\cdot(6435\cos^{8}\theta-12012\cos^{6}\theta+6930\cos^{4}\theta-1260\cos^{2}\theta+35)\\ Y_{8}^{ 1}(\theta,\varphi)&={-3\over 64}\sqrt{17\over 2\pi}\cdot e^{i\varphi}\cdot\sin\theta\cdot(715\cos^{7}\theta-1001\cos^{5}\theta+385\cos^{3}\theta-35\cos\theta)\\ Y_{8}^{ 2}(\theta,\varphi)&={ 3\over 128}\sqrt{595\over \pi}\cdot e^{2i\varphi}\cdot\sin^{2}\theta\cdot(143\cos^{6}\theta-143\cos^{4}\theta+33\cos^{2}\theta-1)\\ Y_{8}^{ 3}(\theta,\varphi)&={-1\over 64}\sqrt{19635\over 2\pi}\cdot e^{3i\varphi}\cdot\sin^{3}\theta\cdot(39\cos^{5}\theta-26\cos^{3}\theta+3\cos\theta)\\ Y_{8}^{ 4}(\theta,\varphi)&={ 3\over 128}\sqrt{1309\over 2\pi}\cdot e^{4i\varphi}\cdot\sin^{4}\theta\cdot(65\cos^{4}\theta-26\cos^{2}\theta+1)\\ Y_{8}^{ 5}(\theta,\varphi)&={-3\over 64}\sqrt{17017\over 2\pi}\cdot e^{5i\varphi}\cdot\sin^{5}\theta\cdot(5\cos^{3}\theta-\cos\theta)\\ Y_{8}^{ 6}(\theta,\varphi)&={ 1\over 128}\sqrt{7293\over \pi}\cdot e^{6i\varphi}\cdot\sin^{6}\theta\cdot(15\cos^{2}\theta-1)\\ Y_{8}^{ 7}(\theta,\varphi)&={-3\over 64}\sqrt{12155\over 2\pi}\cdot e^{7i\varphi}\cdot\sin^{7}\theta\cdot\cos\theta\\ Y_{8}^{ 8}(\theta,\varphi)&={ 3\over 256}\sqrt{12155\over 2\pi}\cdot e^{8i\varphi}\cdot\sin^{8}\theta \end{align} }[/math]

ℓ = 9

[math]\displaystyle{ \begin{align} Y_{9}^{-9}(\theta,\varphi)&={ 1\over 512}\sqrt{230945\over \pi}\cdot e^{-9i\varphi}\cdot\sin^{9}\theta\\ Y_{9}^{-8}(\theta,\varphi)&={ 3\over 256}\sqrt{230945\over 2\pi}\cdot e^{-8i\varphi}\cdot\sin^{8}\theta\cdot\cos\theta\\ Y_{9}^{-7}(\theta,\varphi)&={ 3\over 512}\sqrt{ 13585\over \pi}\cdot e^{-7i\varphi}\cdot\sin^{7}\theta\cdot(17\cos^{2}\theta-1)\\ Y_{9}^{-6}(\theta,\varphi)&={ 1\over 128}\sqrt{ 40755\over \pi}\cdot e^{-6i\varphi}\cdot\sin^{6}\theta\cdot(17\cos^{3}\theta-3\cos\theta)\\ Y_{9}^{-5}(\theta,\varphi)&={ 3\over 256}\sqrt{ 2717\over \pi}\cdot e^{-5i\varphi}\cdot\sin^{5}\theta\cdot(85\cos^{4}\theta-30\cos^{2}\theta+1)\\ Y_{9}^{-4}(\theta,\varphi)&={ 3\over 128}\sqrt{ 95095\over 2\pi}\cdot e^{-4i\varphi}\cdot\sin^{4}\theta\cdot(17\cos^{5}\theta-10\cos^{3}\theta+\cos\theta)\\ Y_{9}^{-3}(\theta,\varphi)&={ 1\over 256}\sqrt{ 21945\over \pi}\cdot e^{-3i\varphi}\cdot\sin^{3}\theta\cdot(221\cos^{6}\theta-195\cos^{4}\theta+39\cos^{2}\theta-1)\\ Y_{9}^{-2}(\theta,\varphi)&={ 3\over 128}\sqrt{ 1045\over \pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\cdot(221\cos^{7}\theta-273\cos^{5}\theta+91\cos^{3}\theta-7\cos\theta)\\ Y_{9}^{-1}(\theta,\varphi)&={ 3\over 256}\sqrt{ 95\over 2\pi}\cdot e^{- i\varphi}\cdot\sin \theta\cdot(2431\cos^{8}\theta-4004\cos^{6}\theta+2002\cos^{4}\theta-308\cos^{2}\theta+7)\\ Y_{9}^{ 0}(\theta,\varphi)&={ 1\over 256}\sqrt{ 19\over \pi}\cdot (12155\cos^{9}\theta-25740\cos^{7}\theta+18018\cos^{5}\theta-4620\cos^{3}\theta+315\cos\theta)\\ Y_{9}^{ 1}(\theta,\varphi)&={-3\over 256}\sqrt{ 95\over 2\pi}\cdot e^{ i\varphi}\cdot\sin \theta\cdot(2431\cos^{8}\theta-4004\cos^{6}\theta+2002\cos^{4}\theta-308\cos^{2}\theta+7)\\ Y_{9}^{ 2}(\theta,\varphi)&={ 3\over 128}\sqrt{ 1045\over \pi}\cdot e^{ 2i\varphi}\cdot\sin^{2}\theta\cdot(221\cos^{7}\theta-273\cos^{5}\theta+91\cos^{3}\theta-7\cos\theta)\\ Y_{9}^{ 3}(\theta,\varphi)&={-1\over 256}\sqrt{ 21945\over \pi}\cdot e^{ 3i\varphi}\cdot\sin^{3}\theta\cdot(221\cos^{6}\theta-195\cos^{4}\theta+39\cos^{2}\theta-1)\\ Y_{9}^{ 4}(\theta,\varphi)&={ 3\over 128}\sqrt{ 95095\over 2\pi}\cdot e^{ 4i\varphi}\cdot\sin^{4}\theta\cdot(17\cos^{5}\theta-10\cos^{3}\theta+\cos\theta)\\ Y_{9}^{ 5}(\theta,\varphi)&={-3\over 256}\sqrt{ 2717\over \pi}\cdot e^{ 5i\varphi}\cdot\sin^{5}\theta\cdot(85\cos^{4}\theta-30\cos^{2}\theta+1)\\ Y_{9}^{ 6}(\theta,\varphi)&={ 1\over 128}\sqrt{ 40755\over \pi}\cdot e^{ 6i\varphi}\cdot\sin^{6}\theta\cdot(17\cos^{3}\theta-3\cos\theta)\\ Y_{9}^{ 7}(\theta,\varphi)&={-3\over 512}\sqrt{ 13585\over \pi}\cdot e^{ 7i\varphi}\cdot\sin^{7}\theta\cdot(17\cos^{2}\theta-1)\\ Y_{9}^{ 8}(\theta,\varphi)&={ 3\over 256}\sqrt{230945\over 2\pi}\cdot e^{ 8i\varphi}\cdot\sin^{8}\theta\cdot\cos\theta\\ Y_{9}^{ 9}(\theta,\varphi)&={-1\over 512}\sqrt{230945\over \pi}\cdot e^{ 9i\varphi}\cdot\sin^{9}\theta \end{align} }[/math]

ℓ = 10

[math]\displaystyle{ \begin{align} Y_{10}^{-10}(\theta,\varphi)&={1\over 1024}\sqrt{969969\over \pi}\cdot e^{-10i\varphi}\cdot\sin^{10}\theta\\ Y_{10}^{- 9}(\theta,\varphi)&={1\over 512}\sqrt{4849845\over \pi}\cdot e^{-9i\varphi}\cdot\sin^{9}\theta\cdot\cos\theta\\ Y_{10}^{- 8}(\theta,\varphi)&={1\over 512}\sqrt{255255\over 2\pi}\cdot e^{-8i\varphi}\cdot\sin^{8}\theta\cdot(19\cos^{2}\theta-1)\\ Y_{10}^{- 7}(\theta,\varphi)&={3\over 512}\sqrt{85085\over \pi}\cdot e^{-7i\varphi}\cdot\sin^{7}\theta\cdot(19\cos^{3}\theta-3\cos\theta)\\ Y_{10}^{- 6}(\theta,\varphi)&={3\over 1024}\sqrt{5005\over \pi}\cdot e^{-6i\varphi}\cdot\sin^{6}\theta\cdot(323\cos^{4}\theta-102\cos^{2}\theta+3)\\ Y_{10}^{- 5}(\theta,\varphi)&={3\over 256}\sqrt{1001\over \pi}\cdot e^{-5i\varphi}\cdot\sin^{5}\theta\cdot(323\cos^{5}\theta-170\cos^{3}\theta+15\cos\theta)\\ Y_{10}^{- 4}(\theta,\varphi)&={3\over 256}\sqrt{5005\over 2\pi}\cdot e^{-4i\varphi}\cdot\sin^{4}\theta\cdot(323\cos^{6}\theta-255\cos^{4}\theta+45\cos^{2}\theta-1)\\ Y_{10}^{- 3}(\theta,\varphi)&={3\over 256}\sqrt{5005\over \pi}\cdot e^{-3i\varphi}\cdot\sin^{3}\theta\cdot(323\cos^{7}\theta-357\cos^{5}\theta+105\cos^{3}\theta-7\cos\theta)\\ Y_{10}^{- 2}(\theta,\varphi)&={3\over 512}\sqrt{385\over 2\pi}\cdot e^{-2i\varphi}\cdot\sin^{2}\theta\cdot(4199\cos^{8}\theta-6188\cos^{6}\theta+2730\cos^{4}\theta-364\cos^{2}\theta+7)\\ Y_{10}^{- 1}(\theta,\varphi)&={1\over 256}\sqrt{1155\over 2\pi}\cdot e^{-i\varphi}\cdot\sin\theta\cdot(4199\cos^{9}\theta-7956\cos^{7}\theta+4914\cos^{5}\theta-1092\cos^{3}\theta+63\cos\theta)\\ Y_{10}^{ 0}(\theta,\varphi)&={1\over 512}\sqrt{21\over \pi}\cdot(46189\cos^{10}\theta-109395\cos^{8}\theta+90090\cos^{6}\theta-30030\cos^{4}\theta+3465\cos^{2}\theta-63)\\ Y_{10}^{ 1}(\theta,\varphi)&={-1\over 256}\sqrt{1155\over 2\pi}\cdot e^{i\varphi}\cdot\sin\theta\cdot(4199\cos^{9}\theta-7956\cos^{7}\theta+4914\cos^{5}\theta-1092\cos^{3}\theta+63\cos\theta)\\ Y_{10}^{ 2}(\theta,\varphi)&={3\over 512}\sqrt{385\over 2\pi}\cdot e^{2i\varphi}\cdot\sin^{2}\theta\cdot(4199\cos^{8}\theta-6188\cos^{6}\theta+2730\cos^{4}\theta-364\cos^{2}\theta+7)\\ Y_{10}^{ 3}(\theta,\varphi)&={-3\over 256}\sqrt{5005\over \pi}\cdot e^{3i\varphi}\cdot\sin^{3}\theta\cdot(323\cos^{7}\theta-357\cos^{5}\theta+105\cos^{3}\theta-7\cos\theta)\\ Y_{10}^{ 4}(\theta,\varphi)&={3\over 256}\sqrt{5005\over 2\pi}\cdot e^{4i\varphi}\cdot\sin^{4}\theta\cdot(323\cos^{6}\theta-255\cos^{4}\theta+45\cos^{2}\theta-1)\\ Y_{10}^{ 5}(\theta,\varphi)&={-3\over 256}\sqrt{1001\over \pi}\cdot e^{5i\varphi}\cdot\sin^{5}\theta\cdot(323\cos^{5}\theta-170\cos^{3}\theta+15\cos\theta)\\ Y_{10}^{ 6}(\theta,\varphi)&={3\over 1024}\sqrt{5005\over \pi}\cdot e^{6i\varphi}\cdot\sin^{6}\theta\cdot(323\cos^{4}\theta-102\cos^{2}\theta+3)\\ Y_{10}^{ 7}(\theta,\varphi)&={-3\over 512}\sqrt{85085\over \pi}\cdot e^{7i\varphi}\cdot\sin^{7}\theta\cdot(19\cos^{3}\theta-3\cos\theta)\\ Y_{10}^{ 8}(\theta,\varphi)&={1\over 512}\sqrt{255255\over 2\pi}\cdot e^{8i\varphi}\cdot\sin^{8}\theta\cdot(19\cos^{2}\theta-1)\\ Y_{10}^{ 9}(\theta,\varphi)&={-1\over 512}\sqrt{4849845\over \pi}\cdot e^{9i\varphi}\cdot\sin^{9}\theta\cdot\cos\theta\\ Y_{10}^{ 10}(\theta,\varphi)&={1\over 1024}\sqrt{969969\over \pi}\cdot e^{10i\varphi}\cdot\sin^{10}\theta \end{align} }[/math]

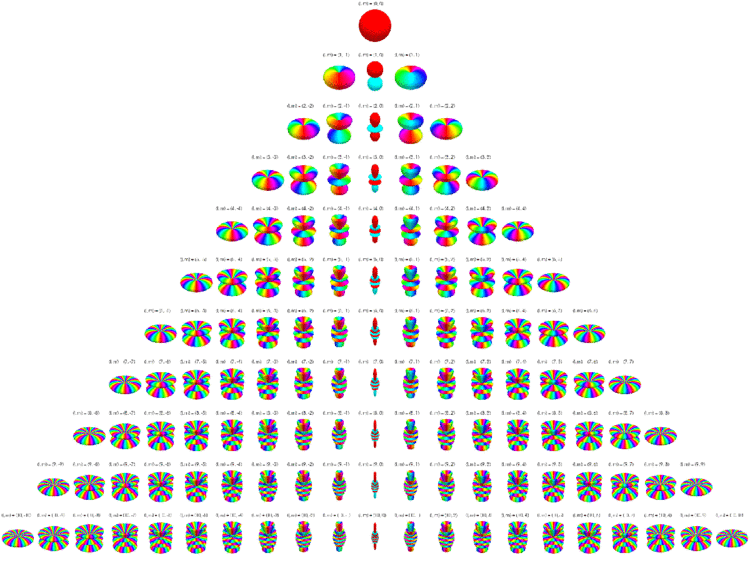
Visualization of complex spherical harmonics

2D polar/azimuthal angle maps

Below the complex spherical harmonics are represented on 2D plots with the azimuthal angle, [math]\displaystyle{ \phi }[/math], on the horizontal axis and the polar angle, [math]\displaystyle{ \theta }[/math], on the vertical axis. The saturation of the color at any point represents the magnitude of the spherical harmonic and the hue represents the phase.

Visual Array of Complex Spherical Harmonics Represented as 2D Theta/Phi Maps

Polar plots

Below the complex spherical harmonics are represented on polar plots. The magnitude of the spherical harmonic at particular polar and azimuthal angles is represented by the saturation of the color at that point and the phase is represented by the hue at that point.

Visual Array of Complex Spherical Harmonics Represented with Polar Plot

Polar plots with magnitude as radius

Below the complex spherical harmonics are represented on polar plots. The magnitude of the spherical harmonic at particular polar and azimuthal angles is represented by the radius of the plot at that point and the phase is represented by the hue at that point.

Visual Array of Complex Spherical Harmonics Represented with Polar Plot with Magnitude Mapped to Radius

Real spherical harmonics

For each real spherical harmonic, the corresponding atomic orbital symbol (s, p, d, f) is reported as well.

For ℓ = 0, …, 3, see.

ℓ = 0

[math]\displaystyle{ Y_{00} = s = Y_0^0 = \frac{1}{2} \sqrt{\frac{1}{\pi}} }[/math]

ℓ = 1

[math]\displaystyle{ \begin{align} Y_{1,-1} & = p_y = i \sqrt{\frac{1}{2}} \left( Y_1^{- 1} + Y_1^1 \right) = \sqrt{\frac{3}{4 \pi}} \cdot \frac{y}{r} = \sqrt{\frac{3}{4 \pi}} \sin( \theta) \sin \varphi \\ Y_{1,0} & = p_z = Y_1^0 = \sqrt{\frac{3}{4 \pi}} \cdot \frac{z}{r} = \sqrt{\frac{3}{4 \pi}} \cos( \theta) \\ Y_{1,1} & = p_x = \sqrt{\frac{1}{2}} \left( Y_1^{- 1} - Y_1^1 \right) = \sqrt{\frac{3}{4 \pi}} \cdot \frac{x}{r} = \sqrt{\frac{3}{4 \pi}} \sin( \theta) \cos \varphi \end{align} }[/math]

ℓ = 2

[math]\displaystyle{ \begin{align} Y_{2,-2} & = d_{xy} = i \sqrt{\frac{1}{2}} \left( Y_2^{- 2} - Y_2^2\right) = \frac{1}{2} \sqrt{\frac{15}{\pi}} \cdot \frac{x y}{r^2} = \frac{1}{4} \sqrt{\frac{15}{\pi}} \sin^{2}\theta \sin(2\varphi) \\ Y_{2,-1} & = d_{yz} = i \sqrt{\frac{1}{2}} \left( Y_2^{- 1} + Y_2^1 \right) = \frac{1}{2} \sqrt{\frac{15}{\pi}} \cdot \frac{y \cdot z}{r^2} = \frac{1}{4} \sqrt{\frac{15}{\pi}} \sin(2 \theta) \sin \varphi \\ Y_{2,0} & = d_{z^2} = Y_2^0 = \frac{1}{4} \sqrt{\frac{5}{\pi}} \cdot \frac{3z^2 - r^2}{r^2} = \frac{1}{4} \sqrt{\frac{5}{\pi}} (3\cos^{2}\theta -1)\\ Y_{2,1} & = d_{xz} = \sqrt{\frac{1}{2}} \left( Y_2^{- 1} - Y_2^1 \right) = \frac{1}{2} \sqrt{\frac{15}{\pi}} \cdot \frac{x \cdot z}{r^2} = \frac{1}{4} \sqrt{\frac{15}{\pi}} \sin(2 \theta) \cos \varphi\\ Y_{2,2} & = d_{x^2-y^2} = \sqrt{\frac{1}{2}} \left( Y_2^{- 2} + Y_2^2 \right) = \frac{1}{4} \sqrt{\frac{15}{\pi}} \cdot \frac{x^2 - y^2 }{r^2} = \frac{1}{4} \sqrt{\frac{15}{\pi}} \sin^{2}\theta \cos(2\varphi) \end{align} }[/math]

ℓ = 3

[math]\displaystyle{ \begin{align} Y_{3,-3} & = f_{y(3x^2-y^2)} = i \sqrt{\frac{1}{2}} \left( Y_3^{- 3} + Y_3^3 \right) = \frac{1}{4} \sqrt{\frac{35}{2 \pi}} \cdot \frac{y \left( 3 x^2 - y^2 \right)}{r^3} \\ Y_{3,-2} & = f_{xyz} = i \sqrt{\frac{1}{2}} \left( Y_3^{- 2} - Y_3^2 \right) = \frac{1}{2} \sqrt{\frac{105}{\pi}} \cdot \frac{xy \cdot z}{r^3} \\ Y_{3,-1} & = f_{yz^2} = i \sqrt{\frac{1}{2}} \left( Y_3^{- 1} + Y_3^1 \right) = \frac{1}{4} \sqrt{\frac{21}{2 \pi}} \cdot \frac{y \cdot (5 z^2 - r^2)}{r^3} \\ Y_{3,0} & = f_{z^3} = Y_3^0 = \frac{1}{4} \sqrt{\frac{7}{\pi}} \cdot \frac{5 z^3 - 3 z r^2}{r^3} \\ Y_{3,1} & = f_{xz^2} = \sqrt{\frac{1}{2}} \left( Y_3^{- 1} - Y_3^1 \right) = \frac{1}{4} \sqrt{\frac{21}{2 \pi}} \cdot \frac{x \cdot (5 z^2 - r^2)}{r^3} \\ Y_{3,2} & = f_{z(x^2-y^2)} = \sqrt{\frac{1}{2}} \left( Y_3^{- 2} + Y_3^2 \right) = \frac{1}{4} \sqrt{\frac{105}{\pi}} \cdot \frac{\left( x^2 - y^2 \right) \cdot z}{r^3} \\ Y_{3,3} & = f_{x(x^2-3y^2)} = \sqrt{\frac{1}{2}} \left( Y_3^{- 3} - Y_3^3 \right) = \frac{1}{4} \sqrt{\frac{35}{2 \pi}} \cdot \frac{x \left( x^2 - 3 y^2 \right)}{r^3} \end{align} }[/math]

ℓ = 4

[math]\displaystyle{ \begin{align} Y_{4,-4} & = i \sqrt{\frac{1}{2}} \left( Y_4^{- 4} - Y_4^4 \right) = \frac{3}{4} \sqrt{\frac{35}{\pi}} \cdot \frac{xy \left( x^2 - y^2 \right)}{r^4} \\ Y_{4,-3} & = i \sqrt{\frac{1}{2}} \left( Y_4^{- 3} + Y_4^3 \right) = \frac{3}{4} \sqrt{\frac{35}{2 \pi}} \cdot \frac{y (3 x^2 - y^2) \cdot z}{r^4} \\ Y_{4,-2} & = i \sqrt{\frac{1}{2}} \left( Y_4^{- 2} - Y_4^2 \right) = \frac{3}{4} \sqrt{\frac{5}{\pi}} \cdot \frac{xy \cdot (7 z^2 - r^2)}{r^4} \\ Y_{4,-1} & = i \sqrt{\frac{1}{2}} \left( Y_4^{- 1} + Y_4^1\right) = \frac{3}{4} \sqrt{\frac{5}{2 \pi}} \cdot \frac{y \cdot (7 z^3 - 3 z r^2)}{r^4} \\ Y_{4,0} & = Y_4^0 = \frac{3}{16} \sqrt{\frac{1}{\pi}} \cdot \frac{35 z^4 - 30 z^2 r^2 + 3 r^4}{r^4} \\ Y_{4,1} & = \sqrt{\frac{1}{2}} \left( Y_4^{- 1} - Y_4^1 \right) = \frac{3}{4} \sqrt{\frac{5}{2 \pi}} \cdot \frac{x \cdot (7 z^3 - 3 z r^2)}{r^4} \\ Y_{4,2} & = \sqrt{\frac{1}{2}} \left( Y_4^{- 2} + Y_4^2 \right) = \frac{3}{8} \sqrt{\frac{5}{\pi}} \cdot \frac{(x^2 - y^2) \cdot (7 z^2 - r^2)}{r^4} \\ Y_{4,3} & = \sqrt{\frac{1}{2}} \left( Y_4^{- 3} - Y_4^3 \right) = \frac{3}{4} \sqrt{\frac{35}{2 \pi}} \cdot \frac{x(x^2 - 3 y^2) \cdot z}{r^4} \\ Y_{4,4} & = \sqrt{\frac{1}{2}} \left( Y_4^{- 4} + Y_4^4 \right) = \frac{3}{16} \sqrt{\frac{35}{\pi}} \cdot \frac{x^2 \left( x^2 - 3 y^2 \right) - y^2 \left( 3 x^2 - y^2 \right)}{r^4} \end{align} }[/math]

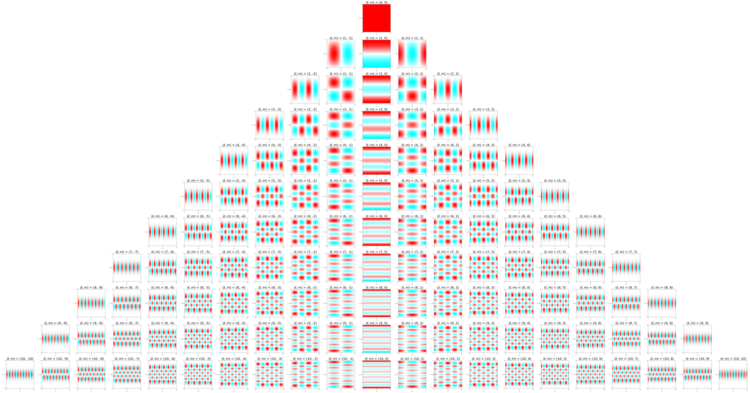
Visualization of real spherical harmonics

2D polar/azimuthal angle maps

Below the real spherical harmonics are represented on 2D plots with the azimuthal angle, [math]\displaystyle{ \phi }[/math], on the horizontal axis and the polar angle, [math]\displaystyle{ \theta }[/math], on the vertical axis. The saturation of the color at any point represents the magnitude of the spherical harmonic and the hue represents the phase.

Visual Array of Real Spherical Harmonics Represented as 2D Theta/Phi Maps

Polar plots

Below the real spherical harmonics are represented on polar plots. The magnitude of the spherical harmonic at particular polar and azimuthal angles is represented by the saturation of the color at that point and the phase is represented by the hue at that point.

Visual Array of Real Spherical Harmonics Represented with Polar Plot

Polar plots with magnitude as radius

Below the real spherical harmonics are represented on polar plots. The magnitude of the spherical harmonic at particular polar and azimuthal angles is represented by the radius of the plot at that point and the phase is represented by the hue at that point.

Visual Array of Real Spherical Harmonics Represented with Polar Plot with Magnitude Mapped to Radius

Polar plots with amplitude as elevation

Below the real spherical harmonics are represented on polar plots. The amplitude of the spherical harmonic (magnitude and sign) at a particular polar and azimuthal angle is represented by the elevation of the plot at that point above or below the surface of a uniform sphere. The magnitude is also represented by the saturation of the color at a given point. The phase is represented by the hue at a given point.

Visual Array of Real Spherical Harmonics Represented with Polar Plot with Amplitude Mapped to Elevation and Saturation

See also

• Spherical harmonics

External links

• Spherical Harmonics at MathWorld
• Spherical Harmonics 3D representation

References

General references

• See section 3 in Mathar, R. J. (2009). "Zernike basis to cartesian transformations". Serbian Astronomical Journal 179 (179): 107–120. doi:10.2298/SAJ0979107M. Bibcode: 2009SerAJ.179..107M.  (see section 3.3)
• For complex spherical harmonics, see also SphericalHarmonicY[l,m,theta,phi] at Wolfram Alpha, especially for specific values of l and m.