Second-order cone programming

From HandWiki
Revision as of 19:15, 6 February 2024 by Len Stevenson (talk | contribs) (add)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

A second-order cone program (SOCP) is a convex optimization problem of the form

minimize [math]\displaystyle{ \ f^T x \ }[/math]
subject to
[math]\displaystyle{ \lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i,\quad i = 1,\dots,m }[/math]
[math]\displaystyle{ Fx = g \ }[/math]

where the problem parameters are [math]\displaystyle{ f \in \mathbb{R}^n, \ A_i \in \mathbb{R}^{{n_i}\times n}, \ b_i \in \mathbb{R}^{n_i}, \ c_i \in \mathbb{R}^n, \ d_i \in \mathbb{R}, \ F \in \mathbb{R}^{p\times n} }[/math], and [math]\displaystyle{ g \in \mathbb{R}^p }[/math]. [math]\displaystyle{ x\in\mathbb{R}^n }[/math] is the optimization variable. [math]\displaystyle{ \lVert x \rVert_2 }[/math] is the Euclidean norm and [math]\displaystyle{ ^T }[/math] indicates transpose.[1] The "second-order cone" in SOCP arises from the constraints, which are equivalent to requiring the affine function [math]\displaystyle{ (A x + b, c^T x + d) }[/math] to lie in the second-order cone in [math]\displaystyle{ \mathbb{R}^{n_i + 1} }[/math].[1]

SOCPs can be solved by interior point methods[2] and in general, can be solved more efficiently than semidefinite programming (SDP) problems.[3] Some engineering applications of SOCP include filter design, antenna array weight design, truss design, and grasping force optimization in robotics.[4] Applications in quantitative finance include portfolio optimization; some market impact constraints, because they are not linear, cannot be solved by quadratic programming but can be formulated as SOCP problems.[5][6][7]

Second-order cone

The standard or unit second-order cone of dimension [math]\displaystyle{ n+1 }[/math] is defined as

[math]\displaystyle{ \mathcal{C}_{n+1}=\left\{ \begin{bmatrix} x \\ t \end{bmatrix} \Bigg| x \in \mathbb{R}^n, t\in \mathbb{R}, \|x\|_2\leq t \right\} }[/math].

The second-order cone is also known by quadratic cone or ice-cream cone or Lorentz cone. The standard second-order cone in [math]\displaystyle{ \mathbb{R}^3 }[/math] is [math]\displaystyle{ \left\{(x,y,z) \Big| \sqrt{x^2 + y^2} \leq z \right\} }[/math].

The set of points satisfying a second-order cone constraint is the inverse image of the unit second-order cone under an affine mapping:

[math]\displaystyle{ \lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow \begin{bmatrix} A_i \\ c_i^T \end{bmatrix} x + \begin{bmatrix} b_i \\ d_i \end{bmatrix} \in \mathcal{C}_{n_i+1} }[/math]

and hence is convex.

The second-order cone can be embedded in the cone of the positive semidefinite matrices since

[math]\displaystyle{ ||x||\leq t \Leftrightarrow \begin{bmatrix} tI & x \\ x^T & t \end{bmatrix} \succcurlyeq 0, }[/math]

i.e., a second-order cone constraint is equivalent to a linear matrix inequality (Here [math]\displaystyle{ M\succcurlyeq 0 }[/math] means [math]\displaystyle{ M }[/math] is semidefinite matrix). Similarly, we also have,

[math]\displaystyle{ \lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow \begin{bmatrix} (c_i^T x+d_i)I & A_i x+b_i \\ (A_i x + b_i)^T & c_i^T x + d_i \end{bmatrix} \succcurlyeq 0 }[/math].

Relation with other optimization problems

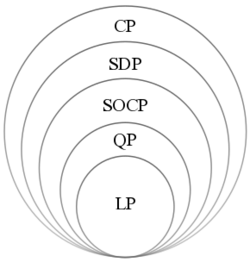
A hierarchy of convex optimization problems. (LP: linear program, QP: quadratic program, SOCP second-order cone program, SDP: semidefinite program, CP: cone program.)

When [math]\displaystyle{ A_i = 0 }[/math] for [math]\displaystyle{ i = 1,\dots,m }[/math], the SOCP reduces to a linear program. When [math]\displaystyle{ c_i = 0 }[/math] for [math]\displaystyle{ i = 1,\dots,m }[/math], the SOCP is equivalent to a convex quadratically constrained linear program.

Convex quadratically constrained quadratic programs can also be formulated as SOCPs by reformulating the objective function as a constraint.[4] Semidefinite programming subsumes SOCPs as the SOCP constraints can be written as linear matrix inequalities (LMI) and can be reformulated as an instance of semidefinite program.[4] The converse, however, is not valid: there are positive semidefinite cones that do not admit any second-order cone representation.[3] In fact, while any closed convex semialgebraic set in the plane can be written as a feasible region of a SOCP,[8] it is known that there exist convex semialgebraic sets that are not representable by SDPs, that is, there exist convex semialgebraic sets that can not be written as a feasible region of a SDP.[9]

Examples

Quadratic constraint

Consider a convex quadratic constraint of the form

[math]\displaystyle{ x^T A x + b^T x + c \leq 0. }[/math]

This is equivalent to the SOCP constraint

[math]\displaystyle{ \lVert A^{1/2} x + \frac{1}{2}A^{-1/2}b \rVert \leq \left(\frac{1}{4}b^T A^{-1} b - c \right)^{\frac{1}{2}} }[/math]

Stochastic linear programming

Consider a stochastic linear program in inequality form

minimize [math]\displaystyle{ \ c^T x \ }[/math]
subject to
[math]\displaystyle{ \mathbb{P}(a_i^Tx \leq b_i) \geq p, \quad i = 1,\dots,m }[/math]

where the parameters [math]\displaystyle{ a_i \ }[/math] are independent Gaussian random vectors with mean [math]\displaystyle{ \bar{a}_i }[/math] and covariance [math]\displaystyle{ \Sigma_i \ }[/math] and [math]\displaystyle{ p\geq0.5 }[/math]. This problem can be expressed as the SOCP

minimize [math]\displaystyle{ \ c^T x \ }[/math]
subject to
[math]\displaystyle{ \bar{a}_i^T x + \Phi^{-1}(p) \lVert \Sigma_i^{1/2} x \rVert_2 \leq b_i , \quad i = 1,\dots,m }[/math]

where [math]\displaystyle{ \Phi^{-1}(\cdot) \ }[/math] is the inverse normal cumulative distribution function.[1]

Stochastic second-order cone programming

We refer to second-order cone programs as deterministic second-order cone programs since data defining them are deterministic. Stochastic second-order cone programs are a class of optimization problems that are defined to handle uncertainty in data defining deterministic second-order cone programs.[10]

Other examples

Other modeling examples are available at the MOSEK modeling cookbook.[11]

Solvers and scripting (programming) languages

Name License Brief info
AMPL commercial An algebraic modeling language with SOCP support
Artelys Knitro commercial
Clarabel open source Native Julia and Rust SOCP solver. Can solve convex problems with arbitrary precision types.
CPLEX commercial
CVXPY open source Python modeling language with support for SOCP. Supports open source and commercial solvers.
CVXOPT open source Convex solver with support for SOCP
ECOS open source SOCP solver optimized for embedded applications
FICO Xpress commercial
Gurobi Optimizer commercial
MATLAB commercial The coneprog function solves SOCP problems[12] using an interior-point algorithm[13]
MOSEK commercial parallel interior-point algorithm
NAG Numerical Library commercial General purpose numerical library with SOCP solver
SCS open source SCS (Splitting Conic Solver) is a numerical optimization package for solving large-scale convex quadratic cone problems.

See also

  • Power cones are generalizations of quadratic cones to powers other than 2.[14]

References

  1. ↑ 1.0 1.1 1.2 Boyd, Stephen; Vandenberghe, Lieven (2004). Convex Optimization. Cambridge University Press. ISBN 978-0-521-83378-3. https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf. Retrieved July 15, 2019. 
  2. ↑ Potra, lorian A.; Wright, Stephen J. (1 December 2000). "Interior-point methods". Journal of Computational and Applied Mathematics 124 (1–2): 281–302. doi:10.1016/S0377-0427(00)00433-7. Bibcode: 2000JCoAM.124..281P. 
  3. ↑ 3.0 3.1 Fawzi, Hamza (2019). "On representing the positive semidefinite cone using the second-order cone" (in en). Mathematical Programming 175 (1–2): 109–118. doi:10.1007/s10107-018-1233-0. ISSN 0025-5610. 
  4. ↑ 4.0 4.1 4.2 Lobo, Miguel Sousa; Vandenberghe, Lieven; Boyd, Stephen; Lebret, Hervé (1998). "Applications of second-order cone programming" (in en). Linear Algebra and Its Applications 284 (1–3): 193–228. doi:10.1016/S0024-3795(98)10032-0. 
  5. ↑ "Solving SOCP". https://docs.mosek.com/slides/2017/shanghai/talk.pdf. 
  6. ↑ "portfolio optimization". https://nmfin.tech/wp-content/uploads/2020/06/new-technologies-in-portfolio-optimization.20200612.pdf. 
  7. ↑ Li, Haksun (16 January 2022). Numerical Methods Using Java: For Data Science, Analysis, and Engineering. APress. pp. Chapter 10. ISBN 978-1484267967. 
  8. ↑ Scheiderer, Claus (2020-04-08). "Second-order cone representation for convex subsets of the plane". arXiv:2004.04196 [math.OC].
  9. ↑ Scheiderer, Claus (2018). "Spectrahedral Shadows" (in en). SIAM Journal on Applied Algebra and Geometry 2 (1): 26–44. doi:10.1137/17M1118981. ISSN 2470-6566. 
  10. ↑ Alzalg, Baha M. (2012-10-01). "Stochastic second-order cone programming: Applications models" (in en). Applied Mathematical Modelling 36 (10): 5122–5134. doi:10.1016/j.apm.2011.12.053. ISSN 0307-904X. https://www.sciencedirect.com/science/article/pii/S0307904X11008547. 
  11. ↑ "MOSEK Modeling Cookbook - Conic Quadratic Optimization". https://docs.mosek.com/modeling-cookbook/cqo.html. 
  12. ↑ "Second-order cone programming solver - MATLAB coneprog". 2021-03-01. https://www.mathworks.com/help/optim/ug/coneprog.html. 
  13. ↑ "Second-Order Cone Programming Algorithm - MATLAB & Simulink". 2021-03-01. https://www.mathworks.com/help/optim/ug/cone-programming-algorithm.html. 
  14. ↑ "MOSEK Modeling Cookbook - the Power Cones". https://docs.mosek.com/modeling-cookbook/powo.html. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Second-order_cone_programming&oldid=3374774"