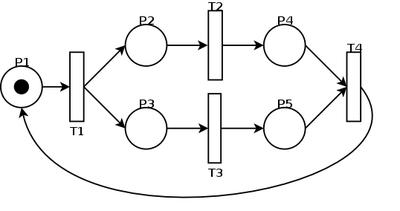
Marked graph

A marked graph is a Petri net in which every place has exactly one incoming arc, and exactly one outgoing arc. This means, that there can not be conflict, but there can be concurrency. Mathematically: [math]\displaystyle{ \forall p\in P: |p\bullet|=|\bullet p|=1 }[/math]. Marked graphs are used mostly to mathematically represent concurrently running operations, such as a multiprocessor machine's internal process state. This class of Petri nets gets the name from a popular way of representing them: as a graph where each place is an edge and each transition is a node.

Uses

Marked graphs are mainly used to mathematically represent concurrent mechanisms, in order to be able to mathematically derive certain characteristics of the design.

Example

This example presents a Marked Graph, where a process is forked at transition T1 and synchronised at T4. In between, two operations take place in non-deterministic fashion, T2 and T3. In fact, Petri nets are so much non-deterministic, that they may not take place at all. But the reason for having this non-deterministic property is not this, but to mimic real-life experiences which shows that parallel computing always means that it is impossible to determine which process/thread will finish first i.e. which operation(s) will execute faster. This can be due to waiting for I/O in real world, or just the different parameters given to the processes/threads.