Adjacent-vertex-distinguishing-total coloring
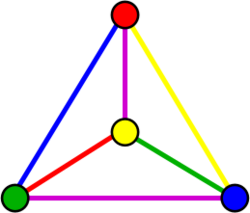
In graph theory, a total coloring is a coloring on the vertices and edges of a graph such that:
(1). no adjacent vertices have the same color;
(2). no adjacent edges have the same color; and
(3). no edge and its endvertices are assigned the same color.
In 2005, Zhang et al.[1] added a restriction to the definition of total coloring and proposed a new type of coloring defined as follows.
Let G = (V,E) be a simple graph endowed with a total coloring φ, and let u be a vertex of G. The set of colors that occurs in the vertex u is defined as C(u) = {φ(u)} ∪ {φ(uv) | uv ∈ E(G)}. Two vertices u,v ∈ V(G) are distinguishable if their color-sets are distinct, i.e., C(u) ≠ C(v).
In graph theory, a total coloring is an adjacent-vertex-distinguishing-total-coloring (AVD-total-coloring) if it has the following additional property:
(4). for every two adjacent vertices u,v of a graph G, their colors-sets are distinct from each other, i.e., C(u) ≠ C(v).
The adjacent-vertex-distinguishing-total-chromatic number χat(G) of a graph G is the fewest colors needed in an AVD-total-coloring of G.
The following lower bound for the AVD-total chromatic number can be obtained from the definition of AVD-total-coloring: If a simple graph G has two adjacent vertices of maximum degree, then χat(G) ≥ Δ(G) + 2.[2] Otherwise, if a simple graph G does not have two adjacent vertices of maximum degree, then χat(G) ≥ Δ(G) + 1.
In 2005, Zhang et al. determined the AVD-total-chromatic number for some classes of graphs, and based in their results they conjectured the following.
AVD-Total-Coloring Conjecture. (Zhang et al.[3])
- χat(G) ≤ Δ(G) + 3.
The AVD-Total-Coloring Conjecture is known to hold for some classes of graphs, such as complete graphs,[4] graphs with Δ=3,[5][6] and all bipartite graphs.[7]
In 2012, Huang et al.[8] showed that χat(G) ≤ 2Δ(G) for any simple graph G with maximum degree Δ(G) > 2. In 2014, Papaioannou and Raftopoulou[9] described an algorithmic procedure that gives a 7-AVD-total-colouring for any 4-regular graph.
Notes
References
- Zhang, Zhong-fu; Chen, Xiang-en; Li, Jingwen; Yao, Bing; Lu, Xinzhong; Wang, Jianfang (2005). "On adjacent-vertex-distinguishing total coloring of graphs". Science China Mathematics 48 (3): 289–299. doi:10.1360/03ys0207. Bibcode: 2005ScChA..48..289Z.
- Hulgan, Jonathan (2009). "Concise proofs for adjacent vertex-distinguishing total colorings". Discrete Mathematics 309 (8): 2548–2550. doi:10.1016/j.disc.2008.06.002.
- Chen, Xiang'en (2008). "On the adjacent vertex distinguishing total coloring numbers of graphs with Delta=3". Discrete Mathematics 308 (17): 4003–4007. doi:10.1016/j.disc.2007.07.091.
- Huang, D.; Wang, W.; Yan, C. (2012). "A note on the adjacent vertex distinguishing total chromatic number of graphs". Discrete Mathematics 312 (24): 3544–3546. doi:10.1016/j.disc.2012.08.006.
- Chen, Meirun; Guo, Xiaofeng (2009). "Adjacent vertex-distinguishing edge and total chromatic numbers of hypercubes". Information Processing Letters 109 (12): 599–602. doi:10.1016/j.ipl.2009.02.006.
- Wang, Yiqiao; Wang, Weifan (2010). "Adjacent vertex distinguishing total colorings of outerplanar graphs". Journal of Combinatorial Optimization 19 (2): 123–133. doi:10.1007/s10878-008-9165-x.
- P. de Mello, Célia; Pedrotti, Vagner (2010). "Adjacent-vertex-distinguishing total coloring of indifference graphs". Matematica Contemporanea 39: 101–110. https://scholar.archive.org/work/ozfu4twm35gnlfzxdt75p2uep4.
- Wang, Weifan; Huang, Danjun (2012). "The adjacent vertex distinguishing total coloring of planar graphs". Journal of Combinatorial Optimization 27 (2): 379. doi:10.1007/s10878-012-9527-2.
- Chen, Xiang-en; Zhang, Zhong-fu (2008). "AVDTC numbers of generalized Halin graphs with maximum degree at least 6". Acta Mathematicae Applicatae Sinica 24 (1): 55–58. doi:10.1007/s10878-012-9527-2.
- Huang, Danjun; Wang, Weifan; Yan, Chengchao (2012). "A note on the adjacent vertex distinguishing total chromatic number of graphs". Discrete Mathematics 312 (24): 3544–3546. doi:10.1016/j.disc.2012.08.006.
- Papaioannou, A.; Raftopoulou, C. (2014). "On the AVDTC of 4-regular graphs". Discrete Mathematics 330: 20–40. doi:10.1016/j.disc.2014.03.019.
- Luiz, Atílio G.; Campos, C.N.; de Mello, C.P. (2015). "AVD-total-colouring of complete equipartite graphs". Discrete Applied Mathematics 184: 189–195. doi:10.1016/j.dam.2014.11.006.
 |

