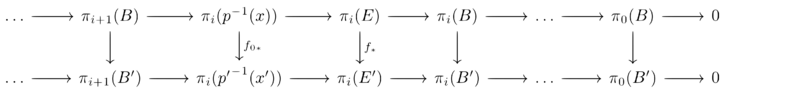Quasi-fibration
In algebraic topology, a quasifibration is a generalisation of fibre bundles and fibrations introduced by Albrecht Dold and René Thom. Roughly speaking, it is a continuous map p: E → B having the same behaviour as a fibration regarding the (relative) homotopy groups of E, B and p−1(x). Equivalently, one can define a quasifibration to be a continuous map such that the inclusion of each fibre into its homotopy fibre is a weak equivalence. One of the main applications of quasifibrations lies in proving the Dold-Thom theorem.
Definition
A continuous surjective map of topological spaces p: E → B is called a quasifibration if it induces isomorphisms
- [math]\displaystyle{ p_*\colon \pi_i(E,p^{-1}(x),y) \to \pi_i(B,x) }[/math]
for all x ∈ B, y ∈ p−1(x) and i ≥ 0. For i = 0,1 one can only speak of bijections between the two sets.
By definition, quasifibrations share a key property of fibrations, namely that a quasifibration p: E → B induces a long exact sequence of homotopy groups
- [math]\displaystyle{ \begin{align} \dots\to \pi_{i+1}(B,x)\to \pi_i(p^{-1}(x),y)\to \pi_i(E,y)&\to \pi_i(B,x)\to \dots \\ &\to \pi_0(B,x)\to 0 \end{align} }[/math]
as follows directly from the long exact sequence for the pair (E, p−1(x)).
This long exact sequence is also functorial in the following sense: Any fibrewise map f: E → E′ induces a morphism between the exact sequences of the pairs (E, p−1(x)) and (E′, p′−1(x)) and therefore a morphism between the exact sequences of a quasifibration. Hence, the diagram
commutes with f0 being the restriction of f to p−1(x) and x′ being an element of the form p′(f(e)) for an e ∈ p−1(x).
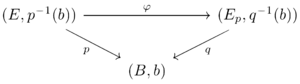
An equivalent definition is saying that a surjective map p: E → B is a quasifibration if the inclusion of the fibre p−1(b) into the homotopy fibre Fb of p over b is a weak equivalence for all b ∈ B. To see this, recall that Fb is the fibre of q under b where q: Ep → B is the usual path fibration construction. Thus, one has
- [math]\displaystyle{ E_p=\{(e,\gamma)\in E\times B^I:\gamma(0)=p(e)\} }[/math]
and q is given by q(e, γ) = γ(1). Now consider the natural homotopy equivalence φ : E → Ep, given by φ(e) = (e, p(e)), where p(e) denotes the corresponding constant path. By definition, p factors through Ep such that one gets a commutative diagram
Applying πn yields the alternative definition.
Examples
- Every Serre fibration is a quasifibration. This follows from the Homotopy lifting property.
- The projection of the letter L onto its base interval is a quasifibration, but not a fibration. More generally, the projection Mf → I of the mapping cylinder of a map f: X → Y between connected CW complexes onto the unit interval is a quasifibration if and only if πi(Mf, p−1(b)) = 0 = πi(I, b) holds for all i ∈ I and b ∈ B. But by the long exact sequence of the pair (Mf, p−1(b)) and by Whitehead's theorem, this is equivalent to f being a homotopy equivalence. For topological spaces X and Y in general, it is equivalent to f being a weak homotopy equivalence. Furthermore, if f is not surjective, non-constant paths in I starting at 0 cannot be lifted to paths starting at a point of Y outside the image of f in Mf. This means that the projection is not a fibration in this case.
- The map SP(p) : SP(X) → SP(X/A) induced by the projection p: X → X/A is a quasifibration for a CW pair (X, A) consisting of two connected spaces. This is one of the main statements used in the proof of the Dold-Thom theorem. In general, this map also fails to be a fibration.
Properties
The following is a direct consequence of the alternative definition of a fibration using the homotopy fibre:
- Theorem. Every quasifibration p: E → B factors through a fibration whose fibres are weakly homotopy equivalent to the ones of p.
A corollary of this theorem is that all fibres of a quasifibration are weakly homotopy equivalent if the base space is path-connected, as this is the case for fibrations.
Checking whether a given map is a quasifibration tends to be quite tedious. The following two theorems are designed to make this problem easier. They will make use of the following notion: Let p: E → B be a continuous map. A subset U ⊂ p(E) is called distinguished (with respect to p) if p: p−1(U) → U is a quasifibration.
- Theorem. If the open subsets U,V and U ∩ V are distinguished with respect to the continuous map p: E → B, then so is U ∪ V.[1]
- Theorem. Let p: E → B be a continuous map where B is the inductive limit of a sequence B1 ⊂ B2 ⊂ ... All Bn are moreover assumed to satisfy the first separation axiom. If all the Bn are distinguished, then p is a quasifibration.
To see that the latter statement holds, one only needs to bear in mind that continuous images of compact sets in B already lie in some Bn. That way, one can reduce it to the case where the assertion is known. These two theorems mean that it suffices to show that a given map is a quasifibration on certain subsets. Then one can patch these together in order to see that it holds on bigger subsets and finally, using a limiting argument, one sees that the map is a quasifibration on the whole space. This procedure has e.g. been used in the proof of the Dold-Thom theorem.
Notes
- ↑ Dold and Thom (1958), Satz 2.2
References
- Aguilar, Marcelo; Gitler, Samuel; Prieto, Carlos (2008). Algebraic Topology from a Homotopical Viewpoint. Springer Science & Business Media. ISBN 978-0-387-22489-3.
- Dold, Albrecht; Lashof, Richard (1959), "Principal Quasifibrations and Fibre Homotopy Equivalence of Bundles", Illinois Journal of Mathematics 2 (2): 285–305
- Dold, Albrecht; Thom, René (1958), "Quasifaserungen und unendliche symmetrische Produkte", Annals of Mathematics, Second Series 67 (2): 239–281, doi:10.2307/1970005, ISSN 0003-486X
- Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 978-0-521-79540-1. http://www.math.cornell.edu/~hatcher/AT/ATpage.html.
- May, J. Peter (1990), "Weak Equivalences and Quasifibrations", Springer Lecture Notes 1425: 91–101
- Piccinini, Renzo A. (1992). Lectures on Homotopy Theory. Elsevier. ISBN 9780080872827.
External links
- Quasifibrations and homotopy pullbacks on MathOverflow
- Quasifibrations from the Lehigh University
 |