MaxCliqueDyn maximum clique algorithm

Developers:	Insilab (National Institute of Chemistry Slovenia)
Development status:	Active
Written in:	C++
Type:	graph theory, maximum clique algorithm, clique problem
License:	GNU General Public License
Website:	insilab.org/maxclique/

The MaxCliqueDyn algorithm is an algorithm for finding a maximum clique in an undirected graph. It is based on a basic algorithm (MaxClique algorithm) which finds a maximum clique of bounded size. The bound is found using an improved coloring algorithm. The MaxCliqueDyn extends MaxClique algorithm to include dynamically varying bounds. This algorithm was designed by Janez Konc and the description was published in 2007. In comparison to earlier algorithms described in the published article the MaxCliqueDyn algorithm is improved by an improved approximate coloring algorithm (ColorSort algorithm) and by applying tighter, more computationally expensive upper bounds on a fraction of the search space. Both improvements reduce time to find maximum clique. In addition to reducing time improved coloring algorithm also reduces the number of steps needed to find a maximum clique.

MaxClique algorithm

The MaxClique algorithm is the basic algorithm of MaxCliqueDyn algorithm. The pseudo code of the algorithm is:

procedure MaxClique(R, C) is
    Q = Ø; Qmax = Ø;

    while R ≠ Ø do
        choose a vertex p with a maximum color C(p) from set R;
        R := R\{p};
        if |Q| + C(p)>|Qmax| then
            Q := Q ⋃ {p};
            if R ⋂ Γ(p) ≠ Ø then
                obtain a vertex-coloring C' of G(R ⋂ Γ(p));
                MaxClique(R ⋂ Γ(p), C');
            else if |Q|>|Qmax| then Qmax:=Q;
            Q := Q\{p};
        else
            return
    end while

where Q is a set of vertices of the currently growing clique, Q_max is a set of vertices of the largest clique currently found, R is a set of candidate vertices and C its corresponding set of color classes. The MaxClique algorithm recursively searches for maximum clique by adding and removing vertices to and from Q.

Coloring algorithm (ColorSort)

In the MaxClique algorithm the approximate coloring algorithm is used to obtain set of color classes C. The ColorSort algorithm is an improved algorithm of the approximate coloring algorithm. In the approximate coloring algorithm vertices are colored one by one in the same order as they appear in a set of candidate vertices R so that if the next vertex p is non-adjacent to all vertices in the some color class it is added to this class and if p is adjacent to at least one vertex in every one of existing color classes it is put into a new color class.

The MaxClique algorithm returns vertices R ordered by their colors. By looking at the MaxClique algorithm it is clear that vertices v ∈ R with colors C(v) < |Q_max| − |Q| + 1 will never be added to the current clique Q. Therefore, sorting those vertices by color is of no use to MaxClique algorithm.

The improved coloring with ColorSort algorithm takes in consideration the above observation. Each vertex is assigned to a color class C_k. If k < |Q_max| − |Q| + 1 the vertex is moved to R (behind the last vertex in R). If k ≥ |Q_max| − |Q| + 1 than the vertex stays in the color class C_k and is not copied to the set R. At the end all of the vertex in color classes C_k where k ≥ |Q_max| − |Q| + 1 are added to the back of set R as they appear in each color class C_k and in increasing order with respect to index k. In Color Sort algorithm only these vertices are assigned colors C(v) = k.

ColorSort algorithm

procedure ColorSort(R, C) is
    max_no := 1;
    kmin := |Qmax| − |Q| + 1;
    if kmin ≤ 0 then kmin := 1;
    j := 0;
    C1 := Ø; C2 := Ø;

    for i := 0 to |R| − 1 do
        p := R[i]; {the i-th vertex in R}
        k := 1;
        while Ck ⋂ Γ(p) ≠ Ø do
            k := k+1;
        if k > max_no then
            max_no := k;
            Cmax_no+1 := Ø;
        end if
        Ck := Ck ⋃ {p};
        if k < kmin then
            R[j] := R[i];
            j := j+1;
        end if
    end for

    C[j−1] := 0;

    for k := kmin to max_no do
        for i := 1 to |Ck| do
            R[j] := Ck[i];
            C[j] := k;
            j := j+1;
        end for
    end for

Example

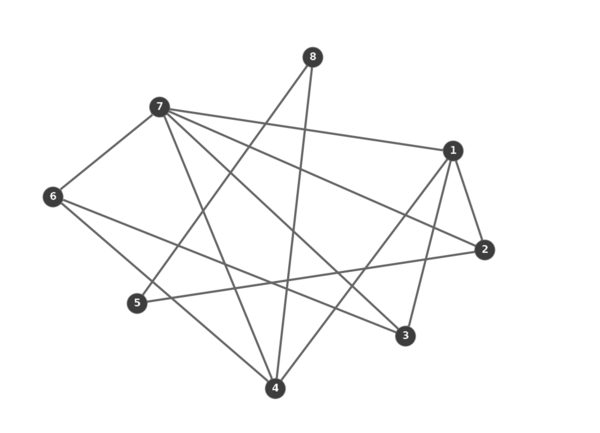
The graph above can be described as candidate set of vertices R = {7⁽⁵⁾, 1⁽⁴⁾, 4⁽⁴⁾, 2⁽³⁾, 3⁽³⁾, 6⁽³⁾, 5⁽²⁾, 8⁽²⁾}. Set of vertices R can now be used as input for both approximate coloring algorithm and ColorSort algorithm. Using any of the two algorithms a table below is constructed.

k	Ck
1	7(5), 5(2)
2	1(4), 6(3), 8(2)
3	4(4), 2(3), 3(3)

The approximate coloring algorithm returns set of vertices R={7⁽⁵⁾, 5⁽²⁾, 1⁽⁴⁾, 6⁽³⁾, 8⁽²⁾, 4⁽⁴⁾, 2⁽³⁾, 3⁽³⁾} and its corresponding set of color classes C = {1,1,2,2,2,3,3,3}. The ColorSort algorithm returns set of vertices R = {7⁽⁵⁾, 1⁽⁴⁾, 6⁽³⁾, 5⁽²⁾, 8⁽²⁾, 4⁽⁴⁾, 2⁽³⁾, 3⁽³⁾} and its corresponding set of color classes C = {–,–,–,–,–,3,3,3}, where – represents unknown color class with k < 3.

MaxCliqueDyn algorithm

The MaxCliqueDyn algorithm is in basic MaxClique algorithm that uses ColorSort algorithm instead approximate coloring algorithm for determining color classes. On each step of MaxClique algorithm the algorithm also recalculates the degrees of vertices in R regarding to the vertex the algorithm is currently in. These vertices are then sorted by decreasing order with respect to their degrees in graph G(R). Then the ColorSort algorithm considers vertices in R sorted by their degrees in the induced graph G(R) rather than in G. By doing so the number of steps required to find the maximum clique is reduced to the minimum. Even so, the overall running time of the MaxClique algorithm is not improved, because computational expense O(|R|²) of the determination of the degrees and sorting of vertices in R stays the same.

MaxCliqueDyn algorithm

procedure MaxCliqueDyn(R, C, level) is
    S[level] := S[level] + S[level−1] − Sold[level];
    Sold[level] := S[level−1];

    while R ≠ Ø do
        choose a vertex p with maximum C(p) (last vertex) from R;
        R := R\{p};
        if |Q| + C[index of p in R] > |Qmax| then
            Q := Q ⋃ {p};
            if R ⋂ Γ(p) ≠ Ø then
                if S[level]/ALL STEPS < Tlimit then
                    calculate the degrees of vertices in G(R ⋂ Γ(p));
                    sort vertices in R ⋂ Γ(p) in a descending order
                    with respect to their degrees;
                end if
                ColorSort(R ⋂ Γ(p), C')
                S[level] := S[level] + 1;
                ALL STEPS := ALL STEPS + 1;
                MaxCliqueDyn(R ⋂ Γ(p), C', level + 1);
            else if |Q| > |Qmax| then Qmax := Q;
            Q := Q\{p};
        else
            return
    end while

Value T_limit can be determined by experimenting on random graphs. In the original article it was determined that algorithm works best for T_limit = 0.025.