Predictive learning
Predictive learning is a machine learning technique where an artificial intelligence model is fed new data to develop an understanding of its environment, capabilities, and limitations. The fields of neuroscience, business, robotics, computer vision, and other fields employ this technique extensively. This concept was developed and expanded by French computer scientist Yann LeCun in 1988 during his career at Bell Labs, where he trained models to detect handwriting so that financial companies could automate check processing.[1] The mathematical foundation for predictive learning dates back to the 17th century, where the British insurance company Lloyd's used predictive analytics models to make a profit.[2] Starting out as a mathematical concept, this concept expanded the possibilities of artificial intelligence. Predictive learning is an attempt to learn with a minimum of pre-existing mental structure. It was inspired by Piaget's account of children constructing knowledge of the world through interaction. Gary Drescher's book 'Made-up Minds' was crucial to the development of this concept.[3]
The idea that predictions and unconscious inference are used by the brain to construct a model of the world, in which it can identify causes of percepts, goes back even further to Hermann von Helmholtz's iteration of this study. Those ideas were later picked up in the field of predictive coding. Another related predictive learning theory is Jeff Hawkins' memory-prediction framework, which is laid out in his book On Intelligence.
Mathematical procedures
Training process
Similar to machine learning, predictive learning aims to extrapolate the value of an unknown dependent variable y, given independent input data x = (x1, x2, … , xn). A set of attributes can be classified into categorical data (immeasurable factors such as race, sex, or affiliation) and numerical data (measurable values such as temperature, annual income, and average speed). Every set of input values is fed into a neural network to predict a value y. In order to predict the output accurately, the weights of the neural network (representing how much each predictor variable affects the outcome) must be incrementally adjusted using stochastic gradient descent to make estimates closer to the actual data.
Once a machine learning model is given enough adjustments and training to predict values closer to the actual values, it should be able to correctly predict outputs of the new data with little error ε, (usually ε < 0.001) compared to the actual data.
Maximizing accuracy
In order to ensure maximum accuracy for a predictive learning model, the predicted values ŷ = F(x), compared to the actual values y, must not exceed a certain error threshold by the risk formula
[math]\displaystyle{ R(F) = E_{xy} }[/math][math]\displaystyle{ L(y, F(x)) }[/math],
where L represents the loss function, y is the actual data, and F(x) is the predicted data. This error function is then used to make incremental adjustments to the model's weights to eventually reach a well-trained prediction of
[math]\displaystyle{ F^{*}(x) = arg min E_{xy} }[/math][math]\displaystyle{ L(y,F(x)) }[/math].[4]
Even if you continuously train a machine learning model, it is impossible to achieve zero error. But if the error is negligible enough, then the model is said to be converged and future predictions will be accurate a vast majority of the time.
Ensemble learning
In some cases, using a singular machine learning approach is not enough to create an accurate estimate for certain data. Ensemble learning is a combination of several machine learning algorithms to create a more accurate estimate. Each machine learning model is represented by the function
F(x) = a0+ [math]\displaystyle{ \sum_{m=1}^{M} }[/math]amfm(x),
where M is the number of methods used, a0 is the bias, am is the weight corresponding to each mth variable, and fm(x) is the activation function corresponding to each variable. An ensemble learning model is represented as a linear combination of the predictions from each constituent approach,
{âm} = arg min [math]\displaystyle{ \sum_{i=1}^{N} }[/math] L(yi,a0+[math]\displaystyle{ \sum_{m=1}^{M} }[/math]amfm(xi)) + λ[math]\displaystyle{ \sum_{i=1}^{N} }[/math]|am|,
where yi is the actual value, the second parameter is the value predicted by each constituent method, and λ is a coefficient representing each model's variation for a certain predictor variable.[4]
Applications
Cognitive development
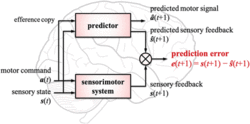
Sensorimotor signals are neural impulses sent to the brain upon physical touch. Using predictive learning to detect sensorimotor signals plays a key role in early cognitive development, as the human brain represents sensorimotor signals in a predictive manner, (it attempts to minimize prediction error between incoming sensory signals and top–down prediction). In order to update an unadjusted predictor, it must be trained through sensorimotor experiences because it does not inherently have prediction ability.[5] In a recent research paper, Dr. Yukie Nagai suggested a new architecture in predictive learning to predict sensorimotor signals based on a two-module approach: a sensorimotor system which interacts with the environment and a predictor which simulates the sensorimotor system in the brain.[5]
Spatiotemporal memory
Computers use predictive learning in spatiotemporal memory to completely create an image given constituent frames. This implementation uses predictive recurrent neural networks, which are neural networks designed to work with sequential data, such as a time series.[6] Using predictive learning in conjunction with computer vision enables computers to create images of their own, which can be helpful when replicating sequential phenomena such as replicating DNA strands, face recognition, or even creating X-ray images.
Social media consumer behavior
In a recent study, data on consumer behavior was collected from various social media platforms such as Facebook, Twitter, LinkedIn, YouTube, Instagram, and Pinterest. The usage of predictive learning analytics led researchers to discover various trends in consumer behavior, such as determining how successful a campaign could be, estimating a fair price for a product to attract consumers, assessing how secure data is, and analyzing the specific audience of the consumers they could target for specific products.[7]
See also
References
- ↑ "Yann LeCun "Predictive Learning: The Next Frontier in AI"" (in en). 2017-02-17. https://www.bell-labs.com/institute/blog/yann-lecun-predictive-learning-next-frontier-ai-february-17-2017/.
- ↑ Corporation, Predictive Success (2019-05-06). "A Brief History of Predictive Analytics" (in en). https://medium.com/@predictivesuccess/a-brief-history-of-predictive-analytics-f05a9e55145f.
- ↑ Drescher, Gary L. (1991) (in en). Made-up Minds: A Constructivist Approach to Artificial Intelligence. MIT Press. ISBN 978-0-262-04120-1. https://books.google.com/books?id=jYsEzeKHLNUC.
- ↑ 4.0 4.1 Friedman, Jerome H.; Popescu, Bogdan E. (2008-09-17). "Predictive learning via rule ensembles". The Annals of Applied Statistics 2 (3): 916–954. doi:10.1214/07-AOAS148. ISSN 1932-6157.
- ↑ 5.0 5.1 Nagai, Yukie (2019-04-29). "Predictive learning: its key role in early cognitive development" (in en). Philosophical Transactions of the Royal Society B: Biological Sciences 374 (1771): 20180030. doi:10.1098/rstb.2018.0030. ISSN 0962-8436. PMID 30852990.
- ↑ Onnen, Heiko (2021-11-01). "Temporal Loops: Intro to Recurrent Neural Networks for Time Series Forecasting in Python" (in en). https://towardsdatascience.com/temporal-loops-intro-to-recurrent-neural-networks-for-time-series-forecasting-in-python-b0398963dc1f.
- ↑ Chaudhary, Kiran; Alam, Mansaf; Al-Rakhami, Mabrook S.; Gumaei, Abdu (2021-05-25). "Machine learning-based mathematical modelling for prediction of social media consumer behavior using big data analytics". Journal of Big Data 8 (1): 73. doi:10.1186/s40537-021-00466-2. ISSN 2196-1115.
 |