Physics:Safety factor (plasma physics)

Short description: Concept in nuclear energy

A diagram depicting the poloidal ([math]\displaystyle{ \theta }[/math]) direction, represented by the red arrow, and the toroidal ([math]\displaystyle{ \zeta }[/math] or [math]\displaystyle{ \phi }[/math]) direction, represented by the blue arrow. The major axis, R, is measured from the center of the hole in the middle to the center of the cylindrical confinement area. The minor axis, r, is the radius of the cylinder.

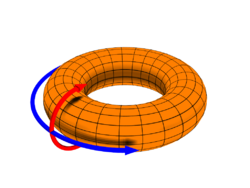
In a toroidal fusion power reactor, the magnetic fields confining the plasma are formed in a helical shape, winding around the interior of the reactor. The safety factor, labeled q or q(r), is the ratio of the times a particular magnetic field line travels around a toroidal confinement area's "long way" (toroidally) to the "short way" (poloidally).

The term "safety" refers to the resulting stability of the plasma; plasmas that rotate around the torus poloidally about the same number of times as toroidally are inherently less susceptible to certain instabilities. The term is most commonly used when referring to tokamak devices. Although the same considerations apply in stellarators, by convention the inverse value is used, the rotational transform, or i.

The concept was first developed by Martin David Kruskal and Vitaly Shafranov, who noticed that the plasma in pinch effect reactors would be stable if q was larger than 1. Macroscopically, this implies that the wavelength of the potential instability is longer than the reactor. This condition is known as the Kruskal–Shafranov limit.

Background

The key concept in magnetic confinement fusion is that ions and electrons in a plasma will rotate around magnetic lines of force. A simple way to confine a plasma would be to use a solenoid, a series of circular magnets mounted along a cylinder that generates uniform lines of force running down the long axis of the cylinder. A plasma generated in the center of the cylinder would be confined to run along the lines down the inside of the tube, keeping it away from the walls. However, it would be free to move along the axis and out the ends of the cylinder.

One can close the ends by bending the solenoid around into a circle, forming a torus (a ring or donut). In this case, the particles will still be confined to the middle of the cylinder, and even if they move along it they would never exit the ends - they would circle the apparatus endlessly. However, Fermi noted a problem with this arrangement; consider a series of circular magnets with the toroidal confinement area threaded through their centers, the magnets will be closer together on the inside of the ring, with a stronger field. Particles in such a system will drift up or down across the torus.

The solution to this problem is to add a secondary magnetic field at right angles to the first. The two magnetic fields will mix to produce a new combined field that is helical, like the stripes on a barber pole. A particle orbiting such a field line will find itself near the outside of the confinement area at some times, and near the inside at others. Although a test particle would always be drifting up (or down) compared to the field, since the field is rotating, that drift will, compared to the confinement chamber, be up or down, in or out, depending on its location along the cylinder. The net effect of the drift over a period of several orbits along the long axis of the reactor nearly adds up to zero.

Rotational transform

The effect of the helical field is to bend the path of a particle so it describes a loop around the cross section of the containment cylinder. At any given point in its orbit around the long axis of the toroid, the particle will be moving at an angle, θ.

In the simple case, when the particle has completed one orbit of the reactor's major axis and returned to its original location, the fields will have made it complete one orbit of the minor axis as well. In this case the rotational transform is 1.

In the more typical case, the fields do not "line up" this way, and the particle will not return to exactly the same location. In this case the rotational transform is calculated thus:

[math]\displaystyle{ i = 2 \pi \cdot \frac{R \cdot B_p}{r \cdot B_t} }[/math]

where R is the major radius, [math]\displaystyle{ r }[/math] the minor radius, [math]\displaystyle{ B_p }[/math] the poloidal field strength, and [math]\displaystyle{ B_t }[/math] the toroidal field. As the fields typically vary with their location within the cylinder, [math]\displaystyle{ i }[/math] varies with location on the minor radius, and is expressed i(r).

Safety factor

In the case of an axisymmetric system, which was common in earlier fusion devices, it is more common to use the safety factor, which is simply the inverse of the rotational transform:

[math]\displaystyle{ q = \frac{2\pi}{i} = \frac{r \cdot B_t}{R \cdot B_p} }[/math]

The safety factor is essentially a measure of the "windiness" of the magnetic fields in a reactor. If the lines are not closed, the safety factor can be expressed as the pitch of the field:

[math]\displaystyle{ q = \frac{d\phi}{d\theta} }[/math]

As the fields vary across the minor axis, q also varies and is often expressed as q(r). On the inside of the cylinder on a typical tokamak it converges on 1, while at the outside it is nearer 6 to 8.

Kruskal–Shafranov limit

Toroidal arrangements are a major class of magnetic fusion energy reactor designs. These are subject to a number of inherent instabilities that cause the plasma to exit the confinement area and hit the walls of the reactor on the order of milliseconds, far too rapidly to be used for energy generation. Among these is the kink instability, which is caused by small variations in the plasma shape. Areas where the plasma is slightly further from the centerline will experience a force outwards, causing a growing bulge that will eventually reach the reactor wall.

These instabilities have a natural pattern based on the rotational transform. This leads to a characteristic wavelength of the kinks, which is based on the ratio of the two magnetic fields that mix to form the twisted field in the plasma. If that wavelength is longer than the long radius of the reactor, then they cannot form. That is, if the length along the major radius [math]\displaystyle{ L_s }[/math] is:

[math]\displaystyle{ L_s = \frac{2 \pi r B_\phi}{B_\theta} \gt 2 \pi R }[/math]

Then the plasma would be stable to this major class of instabilities. Basic mathematical rearrangement, removing the [math]\displaystyle{ 2 \pi }[/math] from both sides and moving the major radius R to the other side of the equality produces:

[math]\displaystyle{ q = \frac{r B_\phi}{R B_\theta} \gt 1 }[/math]

Which produces the simple rule of thumb that as long as the safety factor is greater than one at all points in the plasma, it will be naturally stable to this major class of instabilities. This principle led Soviet researchers to run their toroidal pinch machines with reduced current, leading to the stabilization that provided much higher performance in their T-3 machine in the late 1960s. In more modern machines, the plasma is pressed to the outside section of the chamber, producing a cross sectional shape like a D instead of a circle, which reduces the area with lower safety factor and allows higher currents to be driven through the plasma.

See also

• Troyon limit

References

• Jeffrey Freidberg, "Plasma Physics and Fusion Energy", Cambridge University Press, 2007