Physics:Chézy formula

From HandWiki
Revision as of 23:46, 15 March 2024 by Pchauhan2001 (talk | contribs) (correction)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Fluid dynamics calculation

The Chézy Formula is an semi-empirical resistance equation[1][2] which estimates mean flow velocity in open channel conduits.[3] The relationship was conceptualized and developed in 1768 by French physicist and engineer Antoine de Chézy (1718–1798) while designing Paris's water canal system.[2][4] Chézy discovered a similarity parameter that could be used for estimating flow characteristics in one channel based on the measurements of another.[1] The Chézy formula relates the flow of water through an open channel with the channel's dimensions and slope. The Chézy equation is a pioneering formula in the field of fluid mechanics and was expanded and modified by Irish Engineer Robert Manning in 1889.[1][5][6][7] Manning's modifications to the Chézy formula allowed the entire similarity parameter to be calculated by channel characteristics rather than by experimental measurements. Today, the Chézy and Manning equations continue to accurately estimate open channel fluid flow and are standard formulas in various fields related to fluid mechanics and hydraulics, including physics, mechanical engineering and civil engineering.

The Chézy formula

The Chézy formula describes mean flow velocity in turbulent open channel flow and is used broadly in fields related to fluid mechanics and fluid dynamics.Open channels refer to any open conduit, such as rivers, ditches, canals, or partially full pipes. The Chézy formula is defined for uniform equilibrium and non-uniform gradually varied flows.

The formula is written as:

[math]\displaystyle{ V= C\sqrt{R_hS_0} }[/math]

where,

  • [math]\displaystyle{ V }[/math] is average velocity [length/time];
  • [math]\displaystyle{ R_h }[/math] is the hydraulic radius [length], which is the cross-sectional area of flow divided by the wetted perimeter (for a wide channel this is approximately equal to the water depth); and
  • [math]\displaystyle{ S_0 }[/math] is the hydraulic gradient, which for uniform normal depth of flow is the slope of the channel bottom [unitless; length/length]; and
  • [math]\displaystyle{ C }[/math] is Chézy's coefficient [length1/2/time]. The value of this coefficient must be determined by experiments. The Chézy coefficient ranges typically from 30 m1/2/s (small rough channel) up to 90 m1/2/s (large smooth channel).

The formula is named after Antoine de Chézy, the French hydraulics engineer who devised it in 1775.

For many years following Antoine de Chézy's development of this formula, researchers assumed that [math]\displaystyle{ C }[/math] was a constant independent of flow conditions. However, additional research proved the coefficient's dependence upon both the Reynolds number as well as channel roughness. Accordingly, although the Chézy formula does not appear to incorporate either of these terms, the Chézy coefficient empirically and indirectly represents them.

Hydraulic radius, Rh, is 1/4 the hydraulic diameter and is defined as the area of the flow section divided by the wetted perimeter, P. [1][8]

[math]\displaystyle{ R_h =A/P }[/math]  

Exploring Chézy's similarity parameter

The relationship between linear momentum and deformable fluid bodies is well explored, as are Navier–Stokes equations for incompressible flow. However, exploring the relationships foundational to the Chézy formula can be helpful towards understanding the formula in full.

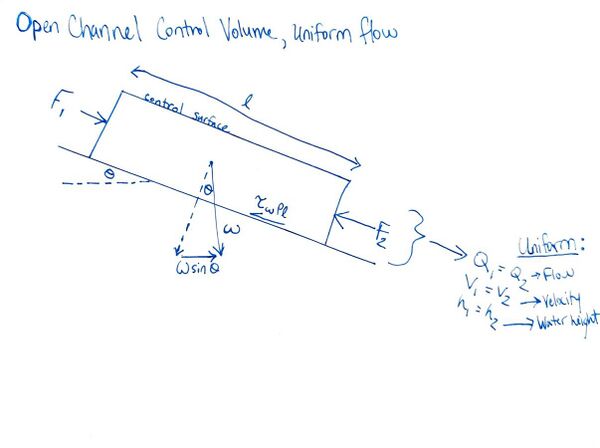
To understand the Chézy similarity parameter, a simple linear momentum equation [1][2] may be considered to summarize the conservation of momentum of a control volume uniformly flowing through an open channel:

[math]\displaystyle{ \sum F_{cv}= {\partial\over\partial t} \int\limits_{CV} V\rho \, {dV} + \int\limits_{CS} V\rho V \cdot \hat{n} \, {dA} }[/math] [1][2]

Where the sum of forces on the contents of a control volume in the open channel are equal to the sum of the time rate of change of the linear momentum of the contents of the control volume, plus the net rate of flow of linear momentum through the control surface.[1] The momentum principle may always used for hydrodynamic force calculations.[2]

When applying the linear momentum equation to a river channel flowing in one dimension, so long as uniform flow is assumed, momentum remains conserved and forces are balanced in the direction of flow:

[math]\displaystyle{ \sum F_{x}=0 =F_1 - F_2 - \tau_wPl +W\sin\theta }[/math] [1][2]

where the hydrostatic pressure forces F1 and F2, the component (τwPl) representing the shear force of friction acting on the control volume, and the component (ω sin θ) representing the gravitational force of the fluid's weight acting on the sloped channel bottom are held in balance in the flow direction.[1] The below free-body diagram illustrates this equilibrium of forces in open channel flow with uniform flow conditions.

A free-body diagram illustrating the equilibrium of forces in the direction of flow of a control volume in an open channel with uniform flow conditions.
This free-body diagram illustrates the equilibrium of forces in the direction of flow of a control volume in an open channel with uniform flow conditions.

Most open-channel flows are turbulent and characterized with very large Reynolds numbers. Due to the large Reynolds numbers characteristic in open channel flow, the channel shear stress proves to be proportional to the density and velocity of the flow.[1][2] This can be illustrated in a series of advanced formulas which identify a shear stress similarity parameter characteristic of all turbulent open channels. Combining this parameter with channel components and the conservation of momentum in an open channel flow, we result with the Chézy formula explaining this relationship: [math]\displaystyle{ V= C\sqrt{R_hS_0} }[/math] .[1][2]

Chézy's similarity parameter and formula explain how the velocity of water flowing through a channel has a relationship with the slope and sheer stress of the channel bottom, the hydraulic radius of flow, and the Chézy coefficient which empirically incorporates several other parameters of the flowing water.This relationship is driven by the conservation of momentum present during uniform flow conditions.

Chézy's formula inspires the Manning formula

Once this relationship was established by Chézy, many engineers and physicists (see the below section Authors of flow formulas)[7][9] continued to search for ways to improve Chézy's equation. A slight oversight of Chézy's formula was determined by the research of these colleagues.[1][7][9] They determined that the velocity's slope dependence in Chézy's formula (V:S0) was reasonable, but that the velocity's dependence on the hydraulic radius (V:Rh1/2) was not, and that the relationship was closer to (V:Rh2/3).[1][7][9] Many compelling formulas based on Chézy's formula have been developed since its discovery by these contemporaries and others, where differing formulas are more suitable in differing conditions.[1][7][9]

Most notably, the Chézy formula provided a substantial foundation for a new flow formula proposed in 1889 by Irish engineer Robert Manning. Manning's formula is a modified Chézy formula that combined many of his aforementioned contemporaries' work.[6][7] Manning's modifications to the Chézy formula allowed the entire similarity parameter to be calculated by channel characteristics rather than by experimental measurements.[1] The Manning equation improved Chézy's equation by better representing the relationship between Rh and velocity, while also replacing the empirical Chézy coefficient ([math]\displaystyle{ C }[/math]) with the Manning resistance coefficient ([math]\displaystyle{ n }[/math]), also referenced in places as the Manning roughness coefficient.[3] Unlike the Chézy coefficient ([math]\displaystyle{ C }[/math]) which could only be determined by field measurements, the Manning coefficient ([math]\displaystyle{ n }[/math]) was determined to remain constant based on the material of the wetted perimeter, allowing for a standardized table of values to be developed that could reasonably estimate flow velocity.[1][3] While field measurements remain the most precise way to obtain either Chézy or Manning coefficients, the standardized values that were developed with the use of the Manning formula provided a much-desired simplicity to open-channel flow estimates.

Chézy formula vs Manning formula

The Manning formula is described excellently elsewhere, but is included below for comparison purposes. Below, the minor modifications used by the Manning formula to improve upon the Chézy formula are clear.

[math]\displaystyle{ V= C\sqrt{R_hS_0} }[/math]      [math]\displaystyle{ V = \frac{{R_h}^{2/3}S_0^{1/2}}{n} \, }[/math]

Chézy formula      Manning formula

Using Chézy formula with Manning coefficient

This similarity between the Chézy and Manning formulas shown above also means that the standardized Manning coefficients may be used to estimate open channel flow velocity with the Chézy formula,[1][2][7] by using them to calculate the Chézy's coefficient as shown below. Manning derived[5] the following relationship between Manning coefficient ([math]\displaystyle{ n }[/math]) to Chézy coefficient ([math]\displaystyle{ C }[/math]) based upon experiments:

[math]\displaystyle{ C = k\left [\frac{1}{n}R_h^{1/6}\right] }[/math][1][7]

where

  • [math]\displaystyle{ C }[/math] is the Chézy coefficient [length1/2/time], a function of relative roughness and Reynolds number;[2]
  • [math]\displaystyle{ R }[/math] is the hydraulic radius, which is the cross-sectional area of flow divided by the wetted perimeter (for a wide channel this approximately equal to the water depth) [m];
  • [math]\displaystyle{ n }[/math] is Manning's coefficient [time/length1/3]; and
  • [math]\displaystyle{ k }[/math] is a constant; k = 1 when using SI units and k = 1.49 when using BG units.

Modern use of Chézy and Manning formulas

Both formulas are widely taught and used in modern times. As both equations reference a single control volume location along the channel, neither address friction factor or head loss[7] directly, but change in pressure head may be calculated by combining them with other formulas such as the Darcy–Weisbach equation.[2] The empirical aspect to the [math]\displaystyle{ C }[/math] coefficient indirectly addresses friction factor and Reynold's number, and is the reason why the Chézy formula remains most accurate in certain conditions, such as river channels with non-uniform channel dimensions.[2] Additionally, both equations are explicitly used with uniform or "steady-state" flow where the hydraulic depth is constant, due to their derivation from the conservation of momentum.[2] In contrast, if the hydraulic conditions fluctuate in open channel flow, they are then described as gradually or rapidly varied flow,[7] and will require further analyses beyond these two formula methods.

As partially full pipes are by definition open channels, so long as they aren't pressurized, the Manning and Chézy formulas may also be used to calculate partially full pipe flow,[2][10][11] but remember that these formulas are intended for uniform and turbulent flow. Many other formulas that have been developed since these two may produce more accurate pipe flow results, such as the Darcy–Weisbach equation or the Hazen–Williams equation, but lack the simplicity of the Manning or Chézy formulas.

Both formulas continue to be broadly taught and used as foundational to open channel and fluid dynamics research. Today, the Manning formula is likely the most globally used formula for open channel uniform flow analysis, due greatly to its simplicity, proven efficacy, and the fact that most open channel studies are concerned with turbulent flow.[12] However, the Chézy's formula is one of the oldest in the field of fluid mechanics,[1] it applies to a wider range of flows than the Manning equation,[13] and its influence continues to this day.

Authors of flow formulas

See also

References

  1. ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 Munson, Bruce Roy (2016). Munson, Young, and Okiishi's Fundamentals of fluid mechanics. Philip M. Gerhart, Andrew L. Gerhart, John I. Hochstein, Donald F. Young, T. H. Okiishi (8th ed.). Hoboken, NJ. ISBN 978-1-119-08070-1. OCLC 916723577. https://www.worldcat.org/oclc/916723577. 
  2. ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 Chanson, Hubert (2004). Hydraulics of Open Channel Flow.. Elsevier. ISBN 978-0-08-047297-3. OCLC 476042721. http://worldcat.org/oclc/476042721. 
  3. ↑ 3.0 3.1 3.2 "Chezys Conduit Flow Equation". https://www.engineeringtoolbox.com/chezy-formula-d_964.html. 
  4. ↑ "Chezys Formula | Encyclopedia.com". https://www.encyclopedia.com/earth-and-environment/ecology-and-environmentalism/environmental-studies/chezys-formula. 
  5. ↑ 5.0 5.1 Manning, R., "On the flow of Water in Open Channels and Pipes." Transactions Institute of Civil Engineers of Ireland, vol. 20, pp. 161–209, Dublin, 1891, Supplement, vol 24, pp. 179–207, 1895
  6. ↑ 6.0 6.1 Rouse, Hunter (1980). History of hydraulics. Iowa Institute of Hydraulic Research. OCLC 314087644. http://worldcat.org/oclc/314087644. 
  7. ↑ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8 7.9 "Dimensionally Homogeneous Form of the Chezy and Manning Equations" (in en-US). 2014-04-24. https://www.hydroreview.com/world-regions/dimensionally-homogeneous-form-of-the-chezy-and-manning-equations/. 
  8. ↑ "USBR Water Measurement Manual – Chapter 2 – Basic Concepts Related to Flowing Water and Measurement, Section 11. Hydraulic Mean Depth and Hydraulic Radius". https://www.usbr.gov/tsc/techreferences/mands/wmm/chap02_11.html. 
  9. ↑ 9.0 9.1 9.2 9.3 "w james notable folks in water engineering". https://www.chiwater.com/Company/Staff/WJamesWebpage/original/homepage/Professional/Heros.html. 
  10. ↑ Bengtson, PhD, P.E., Harlan H.. "Spreadsheet Use for Partially Full Pipe Flow Calculations". https://www.cedengineering.com/userfiles/Partially%20Full%20Pipe%20Flow%20Calculations.pdf. 
  11. ↑ "Partially Full Pipe Flow Calculator and Equations". https://www.engineersedge.com/fluid_flow/partially_full_pipe_flow_calculation/partiallyfullpipeflow_calculation.htm. 
  12. ↑ "Why is Manning's formula more often used than Chezy formula in open channel flows?" (in en). 2010-09-20. https://www.engineeringcivil.com/why-is-manning’s-formula-more-often-used-than-chezy-formula-in-open-channel-flows.html. 
  13. ↑ Cornell University Hydrology Bee 473 (Fall 2004). "Watershed Engineering: Open Channels". http://www.hydrology.bee.cornell.edu/BEE473Homework_files/Openchannel.pdf. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Chézy_formula&oldid=3718160"