Lantern relation
In geometric topology, a branch of mathematics, the lantern relation is a relation that appears between certain Dehn twists in the mapping class group of a surface. The most general version of the relation involves seven Dehn twists. The relation was discovered by Dennis Johnson in 1979.[1]
General form
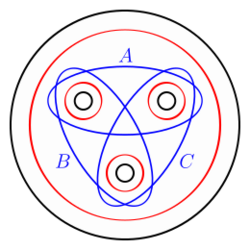
The general form of the lantern relation involves seven Dehn twists in the mapping class group of a disk with three holes,[1][2] as shown in the figure on the right. According to the relation,
- DA DB DC = DR DS DT DU,
where DA, DB, and DC are the right-handed Dehn twists around the blue curves A, B, and C, and DR, DS, DT, DU are the right-handed Dehn twists around the four red curves.
Note that the Dehn twists DR, DS, DT, DU on the right-hand side all commute (since the curves are disjoint, so the order in which they appear does not matter. However, the cyclic order of the three Dehn twists on the left does matter:
- DA DB DC = DB DC DA = DC DA DB.
Also, note that the equalities written above are actually equality up to homotopy or isotopy, as is usual in the mapping class group.
General surfaces
Though we have stated the lantern relation for a disk with three holes, the relation appears in the mapping class group of any surface in which such a disk can be embedded in a nontrivial way. Depending on the setting, some of the Dehn twists appearing in the lantern relation may be homotopic to the identity function, in which case the relation involves fewer than seven Dehn twists.
The lantern relation is used in several different presentations for the mapping class groups of surfaces.
References
- ↑ 1.0 1.1 Johnson, Dennis L. (1979). "Homeomorphisms of a surface which act trivially on homology". Proceedings of the American Mathematical Society (American Mathematical Society) 75 (1): 119–125. doi:10.2307/2042686. https://www.ams.org/proc/1979-075-01/S0002-9939-1979-0529227-4/S0002-9939-1979-0529227-4.pdf.
- ↑ Stipsicz, András; Özbağci, Burak (2004). Surgery on contact 3-manifolds and Stein surfaces. Berlin: Springer. ISBN 3-540-22944-2.
External links
 |