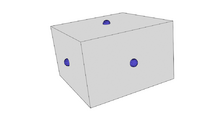
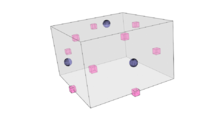
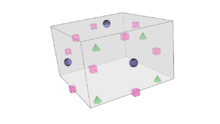
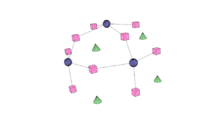
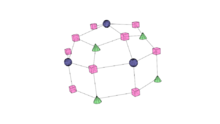
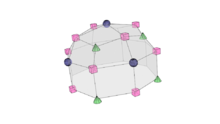
Catmull–Clark subdivision surface
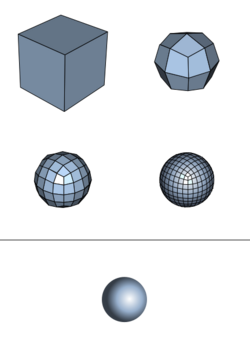
The Catmull–Clark algorithm is a technique used in 3D computer graphics to create curved surfaces by using subdivision surface modeling. It was devised by Edwin Catmull and Jim Clark in 1978 as a generalization of bi-cubic uniform B-spline surfaces to arbitrary topology.[1]
In 2005, Edwin Catmull, together with Tony DeRose and Jos Stam, received an Academy Award for Technical Achievement for their invention and application of subdivision surfaces. DeRose wrote about "efficient, fair interpolation" and character animation. Stam described a technique for a direct evaluation of the limit surface without recursion.
Recursive evaluation
Catmull–Clark surfaces are defined recursively, using the following refinement scheme.[1]
Start with a mesh of an arbitrary polyhedron. All the vertices in this mesh shall be called original points.
- For each face, add a face point
- Set each face point to be the average of all original points for the respective face
- For each edge, add an edge point.
- Set each edge point to be the average of the two neighbouring face points (A,F) and the two endpoints of the edge (M,E) [math]\displaystyle{ \frac{A+F+M+E}{4} }[/math][2]
- For each original point (P), take the average (F) of all n (recently created) face points for faces touching P, and take the average (R) of all n edge midpoints for original edges touching P, where each edge midpoint is the average of its two endpoint vertices (not to be confused with new edge points above). (Note that from the perspective of a vertex P, the number of edges neighboring P is also the number of adjacent faces, hence n)
- Move each original point to the new vertex point [math]\displaystyle{ \frac{F + 2R + (n-3)P}{n} }[/math] (This is the barycenter of P, R and F with respective weights (n − 3), 2 and 1)
- Form edges and faces in the new mesh
- Connect each new face point to the new edge points of all original edges defining the original face
- Connect each new vertex point to the new edge points of all original edges incident on the original vertex
- Define new faces as enclosed by edges
Properties
The new mesh will consist only of quadrilaterals, which in general will not be planar. The new mesh will generally look "smoother" (i.e. less "jagged" or "pointy") than the old mesh. Repeated subdivision results in meshes that are more and more rounded.
The arbitrary-looking barycenter formula was chosen by Catmull and Clark based on the aesthetic appearance of the resulting surfaces rather than on a mathematical derivation, although they do go to great lengths to rigorously show that the method converges to bicubic B-spline surfaces.[1]
It can be shown that the limit surface obtained by this refinement process is at least [math]\displaystyle{ \mathcal{C}^1 }[/math] at extraordinary vertices and [math]\displaystyle{ \mathcal{C}^2 }[/math] everywhere else (when n indicates how many derivatives are continuous, we speak of [math]\displaystyle{ \mathcal{C}^n }[/math] continuity). After one iteration, the number of extraordinary points on the surface remains constant.
Exact evaluation
The limit surface of Catmull–Clark subdivision surfaces can also be evaluated directly, without any recursive refinement. This can be accomplished by means of the technique of Jos Stam (1998).[3] This method reformulates the recursive refinement process into a matrix exponential problem, which can be solved directly by means of matrix diagonalization.
Software using the algorithm
- 3ds Max
- 3D-Coat
- AC3D
- Anim8or
- AutoCAD
- Blender[4]
- Carrara
- CATIA (Imagine and Shape)
- CGAL
- Cheetah3D
- Cinema4D
- Clara.io
- Creo (Freestyle)[5]
- Daz Studio, 2.0
- DeleD Community Edition
- DeleD Designer
- Hammer
- Hexagon
- Houdini
- LightWave 3D, version 9
- Makehuman
- Maya
- Metasequoia
- MODO
- Mudbox
- Power Surfacing add-in for SolidWorks
- Pixar's OpenSubdiv[6][7][8][9][10]
- PRMan
- Realsoft3D
- Remo 3D
- Shade
- Rhinoceros 3D - Grasshopper 3D Plugin - Weaverbird Plugin
- Silo
- SketchUp - Requires a Plugin.
- Softimage XSI
- Strata 3D CX
- Wings 3D
- Zbrush
See also
- Conway polyhedron notation - A set of related topological polyhedron and polygonal mesh operators.
- Doo-Sabin subdivision surface
- Loop subdivision surface
References
- ↑ 1.0 1.1 1.2 Catmull, E.; Clark, J. (1978). "Recursively generated B-spline surfaces on arbitrary topological meshes". Computer-Aided Design 10 (6): 350. doi:10.1016/0010-4485(78)90110-0. http://www.cs.berkeley.edu/~sequin/CS284/PAPERS/CatmullClark_SDSurf.pdf.
- ↑ "Catmull–Clark subdivision surface - Rosetta Code". https://rosettacode.org/wiki/Catmull%E2%80%93Clark_subdivision_surface.
- ↑ Stam, J. (1998). "Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values". Proceedings of the 25th annual conference on Computer graphics and interactive techniques - SIGGRAPH '98. pp. 395–404. doi:10.1145/280814.280945. ISBN 978-0-89791-999-9. http://www.dgp.toronto.edu/people/stam/reality/Research/pdf/sig98.pdf.
- ↑ "Subdivision Surface Modifier". 2020-01-15. https://docs.blender.org/manual/en/latest/modeling/modifiers/generate/subdivision_surface.html.
- ↑ "Archived copy". http://www.ptc.com/File%20Library/Community/Academic%20Program/College_Student_Primer_Creo_2.pdf.
- ↑ Manuel Kraemer (2014). "OpenSubdiv: Interoperating GPU Compute and Drawing". in Martin Watt. Multithreading for Visual Effects. CRC Press. pp. 163–199. ISBN 978-1-4822-4356-7.
- ↑ Meet the Experts: Pixar Animation Studios, The OpenSubdiv Project. YouTube. Archived from the original on 2021-12-11.
- ↑ "Pixar's OpenSubdiv V2: A detailed look". 2013-09-18. http://www.fxguide.com/featured/pixars-opensubdiv-v2-a-detailed-look/.
- ↑ http://on-demand.gputechconf.com/gtc/2014/video/S4856-subdivision-surfaces-industry-standard.mp4[bare URL AV media file]
- ↑ OpenSubdiv Blender demo. YouTube. Archived from the original on 2021-12-11.
Further reading
- Derose, T.; Kass, M.; Truong, T. (1998). "Subdivision surfaces in character animation". Proceedings of the 25th annual conference on Computer graphics and interactive techniques - SIGGRAPH '98. pp. 85. doi:10.1145/280814.280826. ISBN 978-0897919999. http://graphics.pixar.com/library/Geri/paper.pdf.
- Loop, C.; Schaefer, S. (2008). "Approximating Catmull-Clark subdivision surfaces with bicubic patches". ACM Transactions on Graphics 27: 1–11. doi:10.1145/1330511.1330519. http://research.microsoft.com/en-us/um/people/cloop/accTOG.pdf.
- Kovacs, D.; Mitchell, J.; Drone, S.; Zorin, D. (2010). "Real-Time Creased Approximate Subdivision Surfaces with Displacements". IEEE Transactions on Visualization and Computer Graphics 16 (5): 742–51. doi:10.1109/TVCG.2010.31. PMID 20616390. http://www.computer.org/csdl/trans/tg/2010/05/ttg2010050742.pdf. preprint
- Matthias Nießner, Charles Loop, Mark Meyer, Tony DeRose, "Feature Adaptive GPU Rendering of Catmull-Clark Subdivision Surfaces", ACM Transactions on Graphics Volume 31 Issue 1, January 2012, doi:10.1145/2077341.2077347, demo
- Nießner, Matthias; Loop, Charles; Greiner, Günther: Efficient Evaluation of Semi-Smooth Creases in Catmull-Clark Subdivision Surfaces: Eurographics 2012 Annex: Short Papers (Eurographics 2012, Cagliary). 2012, pp 41–44.
- Wade Brainerd, Tessellation in Call of Duty: Ghosts also presented as a SIGGRAPH2014 tutorial [1]
- D. Doo and M. Sabin: Behavior of recursive division surfaces near extraordinary points, Computer-Aided Design, 10 (6) 356–360 (1978), (doi, pdf)
 |