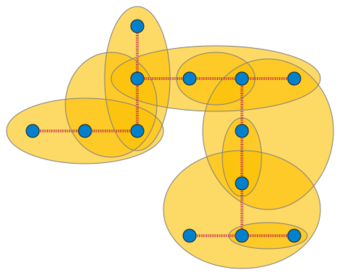
Hypertree

Short description: Generalization of tree graphs to hypergraphs

A hypertree (blue vertices and yellow hyperedges) and its host tree (red)

In the mathematical field of graph theory, a hypergraph H is called a hypertree if it admits a host graph T such that T is a tree. In other words, H is a hypertree if there exists a tree T such that every hyperedge of H is the set of vertices of a connected subtree of T. Hypertrees have also been called arboreal hypergraphs or tree hypergraphs.

Every tree T is itself a hypertree: T itself can be used as the host graph, and every edge of T is a subtree of this host graph. Therefore, hypertrees may be seen as a generalization of the notion of a tree for hypergraphs. They include the connected Berge-acyclic hypergraphs, which have also been used as a (different) generalization of trees for hypergraphs.

Properties

Every hypertree has the Helly property (2-Helly property): if a subset S of its hyperedges has the property that every two hyperedges in S have a nonempty intersection, then S itself has a nonempty intersection (a vertex that belongs to all hyperedges in S).

By results of Duchet, Flament and Slater hypertrees may be equivalently characterized in the following ways.

• A hypergraph H is a hypertree if and only if it has the Helly property and its line graph is a chordal graph.
• A hypergraph H is a hypertree if and only if its dual hypergraph H^* is conformal and the 2-section graph of H^* is chordal.
• A hypergraph is a hypertree if and only if its dual hypergraph is alpha-acyclic in the sense of Fagin.

It is possible to recognize hypertrees (as duals of alpha-acyclic hypergraphs) in linear time. The exact cover problem (finding a set of non-overlapping hyperedges that covers all the vertices) is solvable in polynomial time for hypertrees but remains NP-complete for alpha-acyclic hypergraphs.

See also

• Dually chordal graph, a graph whose maximal cliques form a hypertree

References

• Hypergraphs: Combinatorics of Finite Sets, North-Holland Mathematical Library, 45, Amsterdam: North Holland, 1989, ISBN 0-444-87489-5 .
• "Dually chordal graphs", SIAM Journal on Discrete Mathematics 11: 437–455, 1998, doi:10.1137/s0895480193253415, http://pageperso.lif.univ-mrs.fr/~victor.chepoi/DualChGr.pdf .
• Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy (1999), Graph Classes: A Survey, SIAM Monographs on Discrete Mathematics and Applications, ISBN 0-89871-432-X, https://archive.org/details/graphclassessurv0000bran .
• "Efficient dominating and edge dominating sets for graphs and hypergraphs", Algorithms and Computation: 23rd International Symposium, ISAAC 2012, Taipei, Taiwan, December 19-21, 2012, Proceedings, Lecture Notes in Computer Science, 7676, 2012, pp. 267–277, doi:10.1007/978-3-642-35261-4_30 .
• "Degrees of acyclicity for hypergraphs and relational database schemes", Journal of the ACM 30: 514–550, 1983, doi:10.1145/2402.322390 .
• McKee, T.A.; McMorris, F.R. (1999), Topics in Intersection Graph Theory, SIAM Monographs on Discrete Mathematics and Applications, Philadelphia, PA: Society for Industrial and Applied Mathematics, ISBN 0-89871-430-3 .
• "Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively reduce acyclic hypergraphs", SIAM Journal on Computing 13 (3): 566–579, 1984, doi:10.1137/0213035, http://dml.cz/bitstream/handle/10338.dmlcz/143237/Kybernetika_49-2013-1_2.pdf .
• Voloshin, Vitaly (2002), Coloring Mixed Hypergraphs: Theory, Algorithms and Applications, Fields Institute Monographs, 17, Providence, RI: American Mathematical Society, ISBN 0-8218-2812-6 .