Machin-like formula
In mathematics, Machin-like formulae are a popular technique for computing π (the ratio of the circumference to the diameter of a circle) to a large number of digits. They are generalizations of John Machin's formula from 1706:
- [math]\displaystyle{ \frac{\pi}{4} = 4 \arctan \frac{1}{5} - \arctan \frac{1}{239} }[/math]
which he used to compute π to 100 decimal places.[1][2]
Machin-like formulas have the form
-
[math]\displaystyle{ c_0 \frac{\pi}{4} = \sum_{n=1}^N c_n \arctan \frac{a_n}{b_n} }[/math]
()
where [math]\displaystyle{ c_0 }[/math] is a positive integer, [math]\displaystyle{ c_n }[/math] are signed non-zero integers, and [math]\displaystyle{ a_n }[/math] and [math]\displaystyle{ b_n }[/math] are positive integers such that [math]\displaystyle{ a_n \lt b_n }[/math].
These formulas are used in conjunction with Gregory's series, the Taylor series expansion for arctangent:
-
[math]\displaystyle{ \arctan x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1} = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots }[/math]
()
Derivation
The angle addition formula for arctangent asserts that
-
[math]\displaystyle{ \arctan \frac{a_1}{b_1} + \arctan \frac{a_2}{b_2} = \arctan\frac{a_1 b_2 + a_2 b_1}{b_1 b_2 - a_1 a_2}, }[/math]
()
if [math]\displaystyle{ -\frac{\pi}{2} \lt \arctan \frac{a_1}{b_1} + \arctan \frac{a_2}{b_2} \lt \frac{\pi}{2}. }[/math] All of the Machin-like formulas can be derived by repeated application of equation 3. As an example, we show the derivation of Machin's original formula one has: [math]\displaystyle{ \begin{align} 2 \arctan \frac{1}{5} & = \arctan \frac{1}{5} + \arctan \frac{1}{5} \\ & = \arctan \frac {1\cdot 5 + 1\cdot 5}{5\cdot 5 - 1\cdot 1} \\ & = \arctan \frac {10}{24} \\ & = \arctan \frac {5}{12}, \end{align} }[/math] and consequently [math]\displaystyle{ \begin{align} 4 \arctan \frac{1}{5} & = 2 \arctan \frac{1}{5} + 2 \arctan \frac{1}{5} \\ &= \arctan \frac{5}{12} + \arctan \frac{5}{12} \\ &= \arctan \frac{5\cdot 12 + 5\cdot 12}{12\cdot 12 - 5\cdot 5} \\ &= \arctan \frac{120}{119}. \end{align} }[/math] Therefore also [math]\displaystyle{ \begin{align} 4 \arctan \frac{1}{5} - \frac{\pi}{4} & = 4 \arctan \frac{1}{5} - \arctan \frac{1}{1} \\ &= 4 \arctan \frac{1}{5} + \arctan \frac{-1}{1} \\ &= \arctan \frac{120}{119} + \arctan \frac{-1}{1} \\ &= \arctan \frac{120\cdot 1 + (-1)\cdot 119}{119\cdot 1 - 120\cdot (-1)} \\ &= \arctan \frac{1}{239}, \end{align} }[/math] and so finally [math]\displaystyle{ \frac{\pi}{4} = 4 \arctan \frac{1}{5} - \arctan \frac{1}{239}. }[/math]
An insightful way to visualize equation 3 is to picture what happens when two complex numbers are multiplied together:
- [math]\displaystyle{ (b_1 + a_1 \mathrm{i})\cdot (b_2 + a_2 \mathrm{i}) }[/math]
- [math]\displaystyle{ =b_1 b_2 + a_2 b_1 \mathrm{i} + a_1 b_2 \mathrm{i} - a_1 a_2 }[/math]
-
[math]\displaystyle{ =(b_1 b_2 - a_1 a_2) + (a_1 b_2 + a_2 b_1) \cdot \mathrm{i} }[/math]
()
-
The angle associated with a complex number [math]\displaystyle{ (b_n + a_n \mathrm{i}) }[/math] is given by:
- [math]\displaystyle{ \arctan \frac {a_n}{b_n} }[/math]
Thus, in equation 4, the angle associated with the product is:
- [math]\displaystyle{ \arctan \frac{a_1 b_2 + a_2 b_1}{b_1 b_2 - a_1 a_2} }[/math]
Note that this is the same expression as occurs in equation 3. Thus equation 3 can be interpreted as saying that multiplying two complex numbers means adding their associated angles (see multiplication of complex numbers).
The expression:
- [math]\displaystyle{ c_n \arctan \frac{a_n}{b_n} }[/math]
is the angle associated with:
- [math]\displaystyle{ (b_n + a_n \mathrm{i})^{c_n} }[/math]
Equation 1 can be re-written as:
- [math]\displaystyle{ k \cdot (1 + \mathrm{i})^{c_0} = \prod_{n=1}^N (b_n + a_n \mathrm{i})^{c_n} }[/math]
Here [math]\displaystyle{ k }[/math] is an arbitrary constant that accounts for the difference in magnitude between the vectors on the two sides of the equation. The magnitudes can be ignored, only the angles are significant.
Using complex numbers
Other formulas may be generated using complex numbers.[3] For example, the angle of a complex number [math]\displaystyle{ (a + b \mathrm{i}) }[/math] is given by [math]\displaystyle{ \arctan\frac{b}{a} }[/math] and, when one multiplies complex numbers, one adds their angles. If [math]\displaystyle{ a=b }[/math] then [math]\displaystyle{ \arctan\frac{b}{a} }[/math] is 45 degrees or [math]\displaystyle{ \frac{\pi}{4} }[/math] radians. This means that if the real part and complex part are equal then the arctangent will equal [math]\displaystyle{ \frac{\pi}{4} }[/math]. Since the arctangent of one has a very slow convergence rate if we find two complex numbers that when multiplied will result in the same real and imaginary part we will have a Machin-like formula. An example is [math]\displaystyle{ (2 + \mathrm{i}) }[/math] and [math]\displaystyle{ (3 + \mathrm{i}) }[/math]. If we multiply these out we will get [math]\displaystyle{ (5 + 5 \mathrm{i}) }[/math]. Therefore, [math]\displaystyle{ \arctan\frac{1}{2} + \arctan\frac{1}{3} = \frac{\pi}{4} }[/math].
If you want to use complex numbers to show that [math]\displaystyle{ \frac{\pi}{4} = 4\arctan\frac{1}{5} - \arctan\frac{1}{239} }[/math] you first must know that when multiplying angles you put the complex number to the power of the number that you are multiplying by. So [math]\displaystyle{ (5+\mathrm{i})^4 (239-\mathrm{i}) = (1+\mathrm{i})\cdot 2^2\cdot 13^4 }[/math] and since the real part and imaginary part are equal then, [math]\displaystyle{ 4\arctan\frac{1}{5} - \arctan\frac{1}{239} = \frac{\pi}{4}~. }[/math]
Lehmer's measure
One of the most important parameters that characterize computational efficiency of a Machin-like formula is the Lehmer's measure, defined as[4] [5]
- [math]\displaystyle{ {\it{\lambda}}= \sum_{n=1}^N \frac{1}{\log_{10}(b_n/a_n)} }[/math].
In order to obtain the Lehmer's measure as small as possible, it is necessary to decrease the ratio of positive integers [math]\displaystyle{ a_n/b_n }[/math] in the arctangent arguments and to minimize the number of the terms in the Machin-like formula. Nowadays at [math]\displaystyle{ a_n=1 }[/math] the smallest known Lehmer's measure is [math]\displaystyle{ \lambda\approx 1.51244 }[/math] due to H. Chien-Lih (1997),[6] whose Machin-like formula is shown below. It is very common in the Machin-like formulas when all numerators [math]\displaystyle{ a_n = 1~. }[/math]
Two-term formulas
In the special case where the numerator [math]\displaystyle{ a_n=1 }[/math], there are exactly four solutions having only two terms.[7][8] All four were found by John Machin in 1705–1706, but only one of them became widely known when it was published in William Jones's book Synopsis Palmariorum Matheseos, so the other three are often attributed to other mathematicians. These are
Euler's 1737 (known to Machin 1706):[9][10]
- [math]\displaystyle{ \frac{\pi}{4} = \arctan\frac{1}{2} + \arctan\frac{1}{3} }[/math]
Hermann's 1706 (known to Machin 1706):[11][10]
- [math]\displaystyle{ \frac{\pi}{4} = 2 \arctan\frac{1}{2} - \arctan\frac{1}{7} }[/math]
Hutton's or Vega's (known to Machin 1706):[8][10]
- [math]\displaystyle{ \frac{\pi}{4} = 2 \arctan\frac{1}{3} + \arctan\frac{1}{7} }[/math]
- [math]\displaystyle{ \frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239} }[/math] .
In the general case, where the value of a numerator [math]\displaystyle{ a_n }[/math] is not restricted, there are infinitely many other solutions. For example:
- [math]\displaystyle{ \frac{\pi}{4} = 22 \arctan\frac{1}{28} + \arctan\frac{1744507482180328366854565127}{98646395734210062276153190241239} }[/math]
or
-
[math]\displaystyle{ \frac{\pi}{4} = 22 \arctan\frac{24478}{873121} + 17 \arctan\frac{685601}{69049993} }[/math]
()
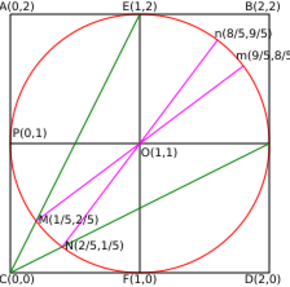
Example
The adjacent diagram demonstrates the relationship between the arctangents and their areas. From the diagram, we have the following:
- [math]\displaystyle{ \begin{array}{ll} {\rm area}(PON)&={\rm area}(MOF)=\pi\times\frac{\angle MOF}{2\pi}=\angle MEF=\arctan{1\over2}\\ {\rm area}(POM)&={\rm area}(NOF)=\arctan{1\over3}\\ {\rm area}(POF)&={\pi\over4}=\arctan{1\over2}+\arctan{1\over3}\\ {\rm area}(MON)&=\arctan{1\over7}\\ \arctan{1\over2}&=\arctan{1\over3}+\arctan{1\over7} , \end{array} }[/math]
a relation which can also be found by means of
the following calculation within the complex numbers
- [math]\displaystyle{ (3+\mathrm{i}) (7+\mathrm{i}) = 21-1 + (3+7)\mathrm{i} = 10\cdot(2+\mathrm{i}) . }[/math]
More terms
The 2002 record for digits of π, 1,241,100,000,000, was obtained by Yasumasa Kanada of Tokyo University. The calculation was performed on a 64-node Hitachi supercomputer with 1 terabyte of main memory, performing 2 trillion operations per second. The following two equations were both used:
- [math]\displaystyle{ \frac{\pi}{4} = 12 \arctan\frac{1}{49} + 32 \arctan\frac{1}{57} - 5 \arctan\frac{1}{239} + 12 \arctan\frac{1}{110443} }[/math]
- Kikuo Takano (1982).
- [math]\displaystyle{ \frac{\pi}{4} = 44 \arctan\frac{1}{57} + 7 \arctan\frac{1}{239} - 12 \arctan\frac{1}{682} + 24 \arctan\frac{1}{12943} }[/math]
- F. C. M. Størmer (1896).
Two equations are used so that one can check they both give the same result; it is helpful if the equations reuse some but not all of the arctangents because those need only be computed once - note the reuse of 57 and 239 above.
Machin-like formulas for π can be constructed by finding a set of numbers where the prime factorisations of b2+1 together use no more distinct primes than the number of elements in the set, and then using either linear algebra or the LLL basis-reduction algorithm to construct linear combinations of arctangents [math]\displaystyle{ \arctan \frac{1}{b_n} }[/math] of reciprocals of integer denominators [math]\displaystyle{ b_n }[/math]. For example, for the Størmer formula above, we have
- [math]\displaystyle{ 57^2+1 = 2 \cdot 5^3 \cdot 13 }[/math]
- [math]\displaystyle{ 239^2+1 = 2 \cdot 13^4 }[/math]
- [math]\displaystyle{ 682^2+1 = 5^3 \cdot 61^2 }[/math]
- [math]\displaystyle{ 12943^2+1 = 2 \cdot 5^4 \cdot 13^3 \cdot 61 }[/math]
so four terms using between them only the primes 2, 5, 13 and 61.
In 1993 Jörg Uwe Arndt[12] found the 11-term formula:
- [math]\displaystyle{ \begin{align} \frac{\pi}{4} =&\; 36462\arctan\frac{1}{390112} + 135908\arctan\frac{1}{485298} + 274509\arctan\frac{1}{683982}\\ & - 39581\arctan\frac{1}{1984933} + 178477\arctan\frac{1}{2478328} - 114569\arctan\frac{1}{3449051}\\ & - 146571\arctan\frac{1}{18975991} + 61914\arctan\frac{1}{22709274} - 69044\arctan\frac{1}{24208144}\\ & - 89431\arctan\frac{1}{201229582} - 43938\arctan\frac{1}{2189376182}\\ \end{align} }[/math]
using the set of 11 primes [math]\displaystyle{ \{2,5,13,17,29,37,53,61,89,97,101\} . }[/math]
Another formula where 10 of the [math]\displaystyle{ \arctan }[/math]-arguments are the same as above has been discovered by Hwang Chien-Lih (黃見利) (2004), so it is easier to check they both give the same result:
- [math]\displaystyle{ \begin{align} \frac{\pi}{4} =&\; 36462\arctan\frac{1}{51387} + 26522\arctan\frac{1}{485298} + 19275\arctan\frac{1}{683982}\\ & - 3119\arctan\frac{1}{1984933} - 3833\arctan\frac{1}{2478328} - 5183\arctan\frac{1}{3449051}\\ & - 37185\arctan\frac{1}{18975991} - 11010\arctan\frac{1}{22709274} + 3880\arctan\frac{1}{24208144}\\ & - 16507\arctan\frac{1}{201229582} - 7476\arctan\frac{1}{2189376182}\\ \end{align} }[/math]
You will note that these formulas reuse all the same arctangents after the first one. They are constructed by looking for numbers where b2+1 is divisible only by primes less than 102.
The most efficient currently known Machin-like formula for computing π is:
- [math]\displaystyle{ \begin{align} \frac{\pi}{4} =&\; 183\arctan\frac{1}{239} + 32\arctan\frac{1}{1023} - 68\arctan\frac{1}{5832}\\ & + 12\arctan\frac{1}{110443} - 12\arctan\frac{1}{4841182} - 100\arctan\frac{1}{6826318}\\ \end{align} }[/math]
- (Hwang Chien-Lih, 1997)
where the set of primes is [math]\displaystyle{ \{2, 5, 13, 229, 457, 1201 \} . }[/math]
A further refinement is to use "Todd's Process", as described in;[5] this leads to results such as
- [math]\displaystyle{ \begin{align} \frac{\pi}{4} =&\; 183\arctan\frac{1}{239} + 32\arctan\frac{1}{1023} - 68\arctan\frac{1}{5832}\\ & + 12\arctan\frac{1}{113021} - 100\arctan\frac{1}{6826318}\\ & - 12\arctan\frac{1}{33366019650} + 12\arctan\frac{1}{43599522992503626068} \\ \end{align} }[/math]
- (Hwang Chien-Lih, 2003)
where the large prime 834312889110521 divides the bn2+1 of the last two indices.
M. Wetherfield found 2004
- [math]\displaystyle{ \begin{align} \frac{\pi}{4} =&\; 83\arctan\frac{1}{107} + 17\arctan\frac{1}{1710} - 22\arctan\frac{1}{103697}\\ & - 24\arctan\frac{1}{2513489} - 44\arctan\frac{1}{18280007883}\\ & + 12\arctan\frac{1}{7939642926390344818}\\ & + 22\arctan\frac{1}{3054211727257704725384731479018} .\\ \end{align} }[/math]
More methods
There are further methods to derive Machin-like formulas for [math]\displaystyle{ \pi }[/math] with reciprocals of integers. One is given by the following formula:[13]
- [math]\displaystyle{ \frac{\pi}{4} = 2^{k-1} \cdot \arctan \frac{1}{A_k} + \sum \limits_{m = 1}^M \arctan \frac{1}{\left \lfloor B_{k,m} \right \rfloor} + \arctan \frac{1}{B_{k,M+1}}, }[/math]
where
- [math]\displaystyle{ a_0 := 0 }[/math]
and recursively
- [math]\displaystyle{ a_k := \sqrt{2 + a_{k - 1}}, \; A_k := \left \lfloor \frac{a_k}{\sqrt{2 - a_{k - 1}}} \right \rfloor }[/math]
and
- [math]\displaystyle{ B_{k,1} := \frac{2}{\left(\dfrac{A_k+\mathrm{i} }{A_k-\mathrm{i} } \right)^{2^{k - 1}} - \mathrm{i}} - \mathrm{i} }[/math]
and recursively
- [math]\displaystyle{ B_{k,m} := \frac{1 + \left \lfloor B_{k,m - 1} \right \rfloor B_{k,m - 1}}{\left \lfloor B_{k,m - 1} \right \rfloor - B_{k,m - 1}} ~. }[/math]
E.g., for [math]\displaystyle{ k = 4 }[/math] and [math]\displaystyle{ M = 5 }[/math] we get:
- [math]\displaystyle{ \begin{align} \frac{\pi }{4} = & \;8 \arctan \frac{1}{10} - \arctan \frac{1}{84} - \arctan \frac{1}{21342}\\ & - \arctan \frac{1}{991268848} - \arctan \frac{1}{193018008592515208050}\\ & - \arctan \frac{1}{197967899896401851763240424238758988350338}\\ & - \arctan \frac{1}{117573868168175352930277752844194126767991915008537018836932014293678271636885792397} \end{align} }[/math]
This is verified by the following MuPAD code:
z:=(10+I)^8*(84-I)*(21342-I)*(991268848-I)*(193018008592515208050-I)\ *(197967899896401851763240424238758988350338-I)\ *(117573868168175352930277752844194126767991915008537018836932014293678271636885792397-I): Re(z)-Im(z) 0
meaning
- [math]\displaystyle{ \begin{align} z:= & \,(10+\mathrm{i})^8\cdot(84-\mathrm{i})\cdot(21342-\mathrm{i})\cdot(991268848-\mathrm{i})\cdot(193018008592515208050-\mathrm{i}) \\ & \cdot(197967899896401851763240424238758988350338-\mathrm{i}) \\ & \cdot(117573868168175352930277752844194126767991915008537018836932014293678271636885792397-\mathrm{i}) \\ \;= & \,(1+\mathrm{i})\cdot \Re(z) ~. \end{align} }[/math]
Efficiency
For large computations of [math]\displaystyle{ \pi }[/math], the binary splitting algorithm can be used to compute the arctangents much, much more quickly than by adding the terms in the Taylor series naively one at a time. In practical implementations such as y-cruncher, there is a relatively large constant overhead per term plus a time proportional to [math]\displaystyle{ 1/\log b_n }[/math], and a point of diminishing returns appears beyond three or four arctangent terms in the sum; this is why the supercomputer calculation above used only a four-term version.
It is not the goal of this section to estimate the actual run time of any given algorithm. Instead, the intention is merely to devise a relative metric by which two algorithms can be compared against each other.
Let [math]\displaystyle{ N_d }[/math] be the number of digits to which [math]\displaystyle{ \pi }[/math] is to be calculated.
Let [math]\displaystyle{ N_t }[/math] be the number of terms in the Taylor series (see equation 2).
Let [math]\displaystyle{ u_n }[/math] be the amount of time spent on each digit (for each term in the Taylor series).
The Taylor series will converge when:
- [math]\displaystyle{ \left(\left(\frac{b_n}{a_n}\right)^2\right)^{N_t} = 10^{N_d} }[/math]
Thus:
- [math]\displaystyle{ N_t = N_d \quad \frac{\ln 10}{2 \ln \frac{b_n}{a_n}} }[/math]
For the first term in the Taylor series, all [math]\displaystyle{ N_d }[/math] digits must be processed. In the last term of the Taylor series, however, there's only one digit remaining to be processed. In all of the intervening terms, the number of digits to be processed can be approximated by linear interpolation. Thus the total is given by:
- [math]\displaystyle{ \frac{N_d N_t}{2} }[/math]
The run time is given by:
- [math]\displaystyle{ \mathit{time} = \frac{u_n N_d N_t}{2} }[/math]
Combining equations, the run time is given by:
- [math]\displaystyle{ \mathit{time} = \frac{u_n {N_d}^2 \ln 10}{4 \ln \frac{b_n}{a_n}} = \frac{k \, u_n}{\ln \frac{b_n}{a_n}} }[/math]
Where [math]\displaystyle{ k }[/math] is a constant that combines all of the other constants. Since this is a relative metric, the value of [math]\displaystyle{ k }[/math] can be ignored.
The total time, across all the terms of equation 1, is given by:
- [math]\displaystyle{ \mathit{time} = \sum_{n=1}^N \frac{u_n}{\ln \frac{b_n}{a_n}} }[/math]
[math]\displaystyle{ u_n }[/math] cannot be modelled accurately without detailed knowledge of the specific software. Regardless, we present one possible model.
The software spends most of its time evaluating the Taylor series from equation 2. The primary loop can be summarized in the following pseudo code:
- [math]\displaystyle{ 1: \quad \mathit{term} \quad *= \quad {a_n}^2 }[/math]
- [math]\displaystyle{ 2: \quad \mathit{term} \quad /= \quad -{b_n}^2 }[/math]
- [math]\displaystyle{ 3: \quad \mathit{tmp} \quad = \quad \mathit{term} \quad / \quad (2*n+1) }[/math]
- [math]\displaystyle{ 4: \quad \mathit{sum} \quad += \quad \mathit{tmp} }[/math]
In this particular model, it is assumed that each of these steps takes approximately the same amount of time. Depending on the software used, this may be a very good approximation or it may be a poor one.
The unit of time is defined such that one step of the pseudo code corresponds to one unit. To execute the loop, in its entirety, requires four units of time. [math]\displaystyle{ u_n }[/math] is defined to be four.
Note, however, that if [math]\displaystyle{ a_n }[/math] is equal to one, then step one can be skipped. The loop only takes three units of time. [math]\displaystyle{ u_n }[/math] is defined to be three.
As an example, consider the equation:
-
[math]\displaystyle{ \frac{\pi}{4} = 44 \arctan \frac{74684}{14967113} + 139 \arctan \frac{1}{239} - 12 \arctan \frac{20138}{15351991} }[/math]
()
The following table shows the estimated time for each of the terms:
| [math]\displaystyle{ a_n }[/math] | [math]\displaystyle{ b_n }[/math] | [math]\displaystyle{ \frac{b_n}{a_n} }[/math] | [math]\displaystyle{ \ln \frac{b_n}{a_n} }[/math] | [math]\displaystyle{ u_n }[/math] | [math]\displaystyle{ \mathit{time} }[/math] |
|---|---|---|---|---|---|
| 74684 | 14967113 | 200.41 | 5.3003 | 4 | 0.75467 |
| 1 | 239 | 239.00 | 5.4765 | 3 | 0.54780 |
| 20138 | 15351991 | 762.34 | 6.6364 | 4 | 0.60274 |
The total time is 0.75467 + 0.54780 + 0.60274 = 1.9052
Compare this with equation 5. The following table shows the estimated time for each of the terms:
| [math]\displaystyle{ a_n }[/math] | [math]\displaystyle{ b_n }[/math] | [math]\displaystyle{ \frac{b_n}{a_n} }[/math] | [math]\displaystyle{ \ln \frac{b_n}{a_n} }[/math] | [math]\displaystyle{ u_n }[/math] | [math]\displaystyle{ \mathit{time} }[/math] |
|---|---|---|---|---|---|
| 24478 | 873121 | 35.670 | 3.5743 | 4 | 1.1191 |
| 685601 | 69049993 | 100.71 | 4.6123 | 4 | 0.8672 |
The total time is 1.1191 + 0.8672 = 1.9863
The conclusion, based on this particular model, is that equation 6 is slightly faster than equation 5, regardless of the fact that equation 6 has more terms. This result is typical of the general trend. The dominant factor is the ratio between [math]\displaystyle{ a_n }[/math] and [math]\displaystyle{ b_n }[/math]. In order to achieve a high ratio, it is necessary to add additional terms. Often, there is a net savings in time.
References
- ↑ 1.0 1.1 Jones, William (1706). Synopsis Palmariorum Matheseos. London: J. Wale. pp. 243, 263. https://archive.org/details/SynopsisPalmariorumMatheseosOrANewIntroductionToTheMathematics/page/n283/. "There are various other ways of finding the Lengths, or Areas of particular Curve Lines or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to Circumference as 1 to
[math]\displaystyle{ \overline{\tfrac{16}5 - \tfrac4{239}} - \tfrac13\overline{\tfrac{16}{5^3} - \tfrac4{239^3}} + \tfrac15\overline{\tfrac{16}{5^5} - \tfrac4{239^5}} -,\, \&c. = }[/math]
3.14159, &c. = π. This Series (among others for the same purpose, and drawn from the same Principle) I receiv'd from the Excellent Analyst, and my much Esteem'd Friend Mr. John Machin; and by means thereof, Van Ceulen's Number, or that in Art. 64.38. may be Examin'd with all desireable Ease and Dispatch."Reprinted in Smith, David Eugene (1929). "William Jones: The First Use of π for the Circle Ratio". A Source Book in Mathematics. McGraw–Hill. pp. 346–347. https://archive.org/details/sourcebookinmath1929smit/page/346/.
- ↑ Beckmann, Petr (1971). A History Of Pi. USA: The Golem Press. p. 102. ISBN 0-88029-418-3. https://archive.org/details/historyofpisymbo00beck/page/102.
- ↑ Størmer, Carl (1897). "Sur l'application de la théorie des nombres entiers complexes a la solution en nombres rationnels [math]\displaystyle{ x_1\ x_2 \ldots x_n }[/math][math]\displaystyle{ c_1\ c_2\ldots c_n }[/math][math]\displaystyle{ k }[/math] de l'équation: [math]\displaystyle{ c_1 \operatorname{arc\ tg}x_1 + {} }[/math][math]\displaystyle{ c_2 \operatorname{arc\ tg}x_2 + \cdots + }[/math][math]\displaystyle{ c_n \operatorname{arc\ tg}x_n = {} }[/math][math]\displaystyle{ k\tfrac\pi4 }[/math]". Archiv for Mathematik og Naturvidenskab 19 (3): 1–95. https://archive.org/details/archivformathema1918961897oslo/page/n122/.
- ↑ Lehmer, Derrick Henry (1938). "On Arccotangent Relations for π". American Mathematical Monthly 45 (10): 657–664. doi:10.2307/2302434.
- ↑ 5.0 5.1 Wetherfield, Michael (2016). "The Enhancement of Machin's Formula by Todd's Process". The Mathematical Gazette 80 (488): 333–344. doi:10.2307/3619567.
- ↑ Chien-Lih, Hwang. "More Machin-Type Identities". The Mathematical Gazette 81 (490).
- ↑ Størmer, Carl (1896). "Solution complète en nombres entiers m, n, x, y et k de l'équation [math]\displaystyle{ m \operatorname{arc\ tg}\tfrac1x + n\operatorname{arc\ tg} \tfrac1y = k\tfrac\pi4. }[/math]". Skrifter udgivne af Videnskabsselskabet i Christiania 1895 (11): 1–21. https://archive.org/details/skrifterudgivnea1895chri/page/n750/.
- ↑ 8.0 8.1 Størmer, Carl (1899). "Solution complète en nombres entiers de l'équation [math]\displaystyle{ m \operatorname{arc\,tang}\frac1x + n \operatorname{arc\,tang}\frac1y = k\frac\pi4 }[/math]" (in fr). Bulletin de la Société Mathématique de France 27: 160–170. doi:10.24033/bsmf.603. https://archive.org/details/bulletinsocit27soci/page/n179/.
- ↑ Euler, Leonhard (1744). "De variis modis circuli quadraturam numeris proxime exprimendi". Commentarii academiae scientiarum Petropolitanae 9: 222-236. E 74. https://archive.org/details/commentariiacade09impe/page/222/.
- ↑ 10.0 10.1 10.2 10.3 Tweddle, Ian (1991). "John Machin and Robert Simson on Inverse-tangent Series for π". Archive for History of Exact Sciences 42 (1): 1-14. doi:10.1007/BF00384331.
- ↑ Letter from Jakob Hermann to Gottfried Leibniz, 21 August 1706. Published in Gerhardt, C.I., ed (1859). "XXII. Hermann an Leibniz.". Leibnizens mathematische Schriften. 4. H.W. Schmidt. pp. 302–304. https://archive.org/details/leibnizensmathe06leibgoog/page/302/.
- ↑ Jörg Uwe Arndt: "Matters Computational" section 32.5.2, page 637.
- ↑ https://arxiv.org/pdf/2108.07718.pdf (2021)
External links
- Weisstein, Eric W.. "Machin-like formulas". http://mathworld.wolfram.com/Machin-LikeFormulas.html.
- The constant π
- Machin's Merit at MathPages
 |