Rybicki Press algorithm
The Rybicki–Press algorithm is a fast algorithm for inverting a matrix whose entries are given by [math]\displaystyle{ A(i,j) = \exp(-a \vert t_i - t_j \vert) }[/math], where [math]\displaystyle{ a \in \mathbb{R} }[/math][1] and where the [math]\displaystyle{ t_i }[/math] are sorted in order.[2] The key observation behind the Rybicki-Press observation is that the matrix inverse of such a matrix is always a tridiagonal matrix (a matrix with nonzero entries only on the main diagonal and the two adjoining ones), and tridiagonal systems of equations can be solved efficiently (to be more precise, in linear time).[1] It is a computational optimization of a general set of statistical methods developed to determine whether two noisy, irregularly sampled data sets are, in fact, dimensionally shifted representations of the same underlying function.[3][4] The most common use of the algorithm is in the detection of periodicity in astronomical observations[verification needed], such as for detecting quasars.[4]
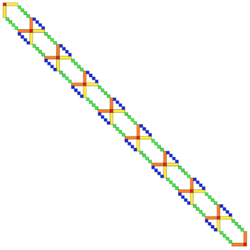
The method has been extended to the Generalized Rybicki-Press algorithm for inverting matrices with entries of the form [math]\displaystyle{ A(i,j) = \sum_{k=1}^p a_k \exp(-\beta_k \vert t_i - t_j \vert) }[/math].[2] The key observation in the Generalized Rybicki-Press (GRP) algorithm is that the matrix [math]\displaystyle{ A }[/math] is a semi-separable matrix with rank [math]\displaystyle{ p }[/math] (that is, a matrix whose upper half, not including the main diagonal, is that of some matrix with matrix rank [math]\displaystyle{ p }[/math] and whose lower half is also that of some possibly different rank [math]\displaystyle{ p }[/math] matrix[2]) and so can be embedded into a larger band matrix (see figure on the right), whose sparsity structure can be leveraged to reduce the computational complexity. As the matrix [math]\displaystyle{ A \in \mathbb{R}^{n\times n} }[/math] has a semi-separable rank of [math]\displaystyle{ p }[/math], the computational complexity of solving the linear system [math]\displaystyle{ Ax=b }[/math] or of calculating the determinant of the matrix [math]\displaystyle{ A }[/math] scales as [math]\displaystyle{ \mathcal{O}\left(p^2n \right) }[/math], thereby making it attractive for large matrices.[2]
The fact that matrix [math]\displaystyle{ A }[/math] is a semi-separable matrix also forms the basis for celerite[5] library, which is a library for fast and scalable Gaussian process regression in one dimension[6] with implementations in C++, Python, and Julia. The celerite method[6] also provides an algorithm for generating samples from a high-dimensional distribution. The method has found attractive applications in a wide range of fields,[which?] especially in astronomical data analysis.[7][8]
See also
- Invertible matrix
- Matrix decomposition
- Multidimensional signal processing
- System of linear equations
References
- ↑ 1.0 1.1 Rybicki, George B.; Press, William H. (1995), "Class of fast methods for processing Irregularly sampled or otherwise inhomogeneous one-dimensional data", Physical Review Letters 74 (7): 1060–1063, doi:10.1103/PhysRevLett.74.1060, PMID 10058924, Bibcode: 1995PhRvL..74.1060R

- ↑ 2.0 2.1 2.2 2.3 Ambikasaran, Sivaram (2015-12-01). "Generalized Rybicki Press algorithm" (in en). Numerical Linear Algebra with Applications 22 (6): 1102–1114. doi:10.1002/nla.2003. ISSN 1099-1506.
- ↑ Rybicki, George B.; Press, William H. (October 1992). "Interpolation, realization, and reconstruction of noisy, irregularly sampled data". The Astrophysical Journal 398: 169. doi:10.1086/171845. Bibcode: 1992ApJ...398..169R.

- ↑ 4.0 4.1 MacLeod, C. L.; Brooks, K.; Ivezic, Z.; Kochanek, C. S.; Gibson, R.; Meisner, A.; Kozlowski, S.; Sesar, B. et al. (2011-02-10). "Quasar Selection Based on Photometric Variability". The Astrophysical Journal 728 (1): 26. doi:10.1088/0004-637X/728/1/26. ISSN 0004-637X. Bibcode: 2011ApJ...728...26M.
- ↑ "celerite — celerite 0.3.0 documentation" (in en). https://celerite.readthedocs.io/en/stable/.
- ↑ 6.0 6.1 Foreman-Mackey, Daniel; Agol, Eric; Ambikasaran, Sivaram; Angus, Ruth (2017). "Fast and Scalable Gaussian Process Modeling with Applications to Astronomical Time Series" (in en). The Astronomical Journal 154 (6): 220. doi:10.3847/1538-3881/aa9332. ISSN 1538-3881. Bibcode: 2017AJ....154..220F. http://stacks.iop.org/1538-3881/154/i=6/a=220.
- ↑ Foreman-Mackey, Daniel (2018). "Scalable Backpropagation for Gaussian Processes using Celerite" (in en). Research Notes of the AAS 2 (1): 31. doi:10.3847/2515-5172/aaaf6c. ISSN 2515-5172. Bibcode: 2018RNAAS...2...31F. http://stacks.iop.org/2515-5172/2/i=1/a=31.
- ↑ Parviainen, Hannu (2018). "Bayesian Methods for Exoplanet Science" (in en). Handbook of Exoplanets. Springer, Cham. pp. 1–24. doi:10.1007/978-3-319-30648-3_149-1. ISBN 9783319306483.
External links
 |