25 great circles of the spherical octahedron

The 25 great circles with domains colored by their symmetry positions

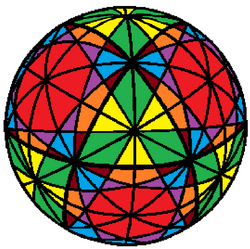
In geometry, the 25 great circles of the spherical octahedron is an arrangement of 25 great circles in octahedral symmetry. It was first identified by Buckminster Fuller and is used in construction of geodesic domes.

Construction

The 25 great circles can be seen in 3 sets: 12, 9, and 4, each representing edges of a polyhedron projected onto a sphere. Nine great circles represent the edges of a disdyakis dodecahedron, the dual of a truncated cuboctahedron. Four more great circles represent the edges of a cuboctahedron, and the last twelve great circles connect edge-centers of the octahedron to centers of other triangles.

See also

• 31 great circles of the spherical icosahedron

References

• Edward Popko, Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere, 2012, pp 21–22. [1]
• Vector Equilibrium and its Transformation Pathways