26-fullerene graph
| 26-fullerene | |
|---|---|
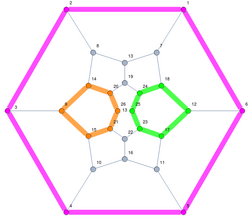 The 26-fullerene graph with its hexagons highlighted | |
| Vertices | 26 |
| Edges | 39 |
| Radius | 5 |
| Diameter | 6 |
| Girth | 5 |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | faces = 3 hexagons, 12 pentagons |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the 26-fullerene graph is a polyhedral graph with V = 26 vertices and E = 39 edges. Its planar embedding has three hexagonal faces (including the one shown as the external face of the illustration) and twelve pentagonal faces. As a planar graph with only pentagonal and hexagonal faces, meeting in three faces per vertex, this graph is a fullerene. The existence of this fullerene has been known since at least 1968.[1]
Properties
The 26-fullerene graph has prismatic symmetry, the same group of symmetries as the triangular prism. This symmetry group has 12 elements; it has six symmetries that arbitrarily permute the three hexagonal faces of the graph and preserve the orientation of its planar embedding, and another six orientation-reversing symmetries.[2]
The number of fullerenes with a given even number of vertices grows quickly in the number of vertices; 26 is the largest number of vertices for which the fullerene structure is unique. The only two smaller fullerenes are the graph of the regular dodecahedron (a fullerene with 20 vertices) and the graph of the truncated hexagonal trapezohedron (a 24-vertex fullerene),[3] which are the two types of cells in the Weaire–Phelan structure.
The 26-fullerene graph has many perfect matchings. One must remove at least five edges from the graph in order to obtain a subgraph that has exactly one perfect matching. This is a unique property of this graph among fullerenes in the sense that, for every other number of vertices of a fullerene, there exists at least one fullerene from which one can remove four edges to obtain a subgraph with a unique perfect matching.[4]
The vertices of the 26-fullerene graph can be labeled with sequences of 12 bits, in such a way that distance in the graph equals half of the Hamming distance between these bitvectors. This can also be interpreted as an isometric embedding from the graph into a 12-dimensional taxicab geometry. The 26-fullerene graph is one of only five fullerenes with such an embedding.[2]
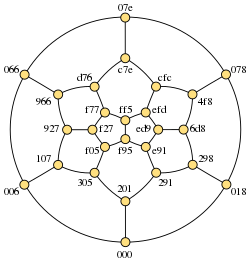
In popular culture
In 2009, The New York Times published a puzzle involving Hamiltonian paths in this graph, taking advantage of the correspondence between its 26 vertices and the 26 letters of the English alphabet.[5][6]
References
- ↑ "Some analogues of Eberhard's theorem on convex polytopes", Israel Journal of Mathematics 6 (4): 398–411 (1969), 1968, doi:10.1007/BF02771220. See line 19 of table, p. 411, completely characterizing which numbers of hexagons are possible in a fullerene.
- ↑ 2.0 2.1 Marcusanu, Mihaela (2007), The classification of -embeddable fullerenes, Ph.D. thesis, Bowling Green State University, ISBN 978-1109-98335-7, http://rave.ohiolink.edu/etdc/view?acc_num=bgsu1180115123. For the embedding, see Figure 5.3, p. 52.
- ↑ Sloane, N. J. A., ed. "Sequence A007894". OEIS Foundation. https://oeis.org/A007894.
- ↑ Yang, Qin; Zhang, Heping; Lin, Yuqing (2015), "On the anti-forcing number of fullerene graphs", MATCH Communications in Mathematical and in Computer Chemistry 74 (3): 673–692
- ↑ Tierney, John (May 4, 2009), "The Hamiltonian Puzzle", The New York Times, https://tierneylab.blogs.nytimes.com/2009/05/04/the-hamiltonian-puzzle
- ↑ Pegg, Ed Jr. (2009), "The Icosian game, revisited", The Mathematica Journal 11 (3): 310–314, doi:10.3888/tmj.11.3-1, http://www.mathematica-journal.com/issue/v11i3/contents/superhamilton/superhamilton.pdf
 |
