Acyclic orientation
In graph theory, an acyclic orientation of an undirected graph is an assignment of a direction to each edge (an orientation) that does not form any directed cycle and therefore makes it into a directed acyclic graph. Every graph has an acyclic orientation.
The chromatic number of any graph equals one more than the length of the longest path in an acyclic orientation chosen to minimize this path length. Acyclic orientations are also related to colorings through the chromatic polynomial, which counts both acyclic orientations and colorings. The planar dual of an acyclic orientation is a totally cyclic orientation, and vice versa. The family of all acyclic orientations can be given the structure of a partial cube by making two orientations adjacent when they differ in the direction of a single edge.
Orientations of trees are always acyclic, and give rise to polytrees. Acyclic orientations of complete graphs are called transitive tournaments. The bipolar orientations are a special case of the acyclic orientations in which there is exactly one source and one sink; every transitive tournament is bipolar.
Construction
Every graph has an acyclic orientation. One way to generate an acyclic orientation is to place the vertices into a sequence, and then direct each edge from the earlier of its endpoints in the sequence to the later endpoint. The vertex sequence then becomes a topological ordering of the resulting directed acyclic graph (DAG), and every topological ordering of this DAG generates the same orientation.
Because every DAG has a topological ordering, every acyclic orientation can be constructed in this way. However, it is possible for different vertex sequences to give rise to the same acyclic orientation, when the resulting DAG has multiple topological orderings. For instance, for a four-vertex cycle graph (shown), there are 24 different vertex sequences, but only 14 possible acyclic orientations.
Relation to coloring
The Gallai–Hasse–Roy–Vitaver theorem states that a graph has an acyclic orientation in which the longest path has at most k vertices if and only if it can be colored with at most k colors.[1]
The number of acyclic orientations may be counted using the chromatic polynomial [math]\displaystyle{ \chi_G }[/math], whose value at a positive integer k is the number of k-colorings of the graph. Every graph G has exactly [math]\displaystyle{ |\chi_G(-1)| }[/math] different acyclic orientations,[2] so in this sense an acyclic orientation can be interpreted as a coloring with −1 colors.
Duality
For planar graphs, acyclic orientations are dual to totally cyclic orientations, orientations in which each edge belongs to a directed cycle: if [math]\displaystyle{ G }[/math] is a planar graph, and orientations of [math]\displaystyle{ G }[/math] are transferred to orientations of the planar dual graph of [math]\displaystyle{ G }[/math] by turning each edge 90 degrees clockwise, then a totally cyclic orientation of [math]\displaystyle{ G }[/math] corresponds in this way to an acyclic orientation of the dual graph and vice versa.[3]
Like the chromatic polynomial, the Tutte polynomial [math]\displaystyle{ T_G }[/math] of a graph [math]\displaystyle{ G }[/math], can be used to count the number of acyclic orientations of [math]\displaystyle{ G }[/math] as [math]\displaystyle{ T_G(2,0) }[/math]. The duality between acyclic and totally cyclic orientations of planar graphs extends in this form to nonplanar graphs as well: the Tutte polynomial of the dual graph of a planar graph is obtained by swapping the arguments of [math]\displaystyle{ T_G }[/math], and the number of totally cyclic orientations of a graph [math]\displaystyle{ G }[/math] is [math]\displaystyle{ T_G(0,2) }[/math], also obtained by swapping the arguments of the formula for the number of acyclic orientations.[4]
Edge flipping
The set of all acyclic orientations of a given graph may be given the structure of a partial cube, in which two acyclic orientations are adjacent whenever they differ in the direction of a single edge.[5] This implies that when two different acyclic orientations of the same graph differ in the directions of k edges, it is possible to transform one of the orientations into the other one by a sequence of k changes of orientation of a single edge, such that each of the intermediate states of this sequence of transformations is also acyclic.
Special cases
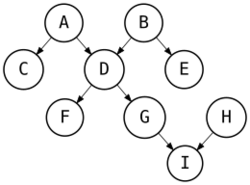
Every orientation of a tree is acyclic. The directed acyclic graph resulting from such an orientation is called a polytree.[6]
An acyclic orientation of a complete graph is called a transitive tournament, and is equivalent to a total ordering of the graph's vertices. In such an orientation there is in particular exactly one source and exactly one sink.
More generally, an acyclic orientation of an arbitrary graph that has a unique source and a unique sink is called a bipolar orientation.[7]
A transitive orientation of a graph is an acyclic orientation that equals its own transitive closure. Not every graph has a transitive orientation; the graphs that do are the comparability graphs.[8] Complete graphs are special cases of comparability graphs, and transitive tournaments are special cases of transitive orientations.
References
- ↑ "Theorem 3.13", Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics, 28, Heidelberg: Springer, 2012, p. 42, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7.
- ↑ Stanley, Richard P. (1973), "Acyclic orientations of graphs", Discrete Mathematics 5 (2): 171–178, doi:10.1016/0012-365X(73)90108-8.
- ↑ Welsh, Dominic (1997), "Approximate counting", Surveys in combinatorics, 1997 (London), London Math. Soc. Lecture Note Ser., 241, Cambridge: Cambridge Univ. Press, pp. 287–323, doi:10.1017/CBO9780511662119.010.
- ↑ "Convexity in oriented matroids", Journal of Combinatorial Theory, Series B 29 (2): 231–243, 1980, doi:10.1016/0095-8956(80)90082-9.
- ↑ Fukuda; Prodon, Alain; Sakuma, Tadashi (2001), "Notes on acyclic orientations and the shelling lemma", Theoretical Computer Science 263 (1–2): 9–16, doi:10.1016/S0304-3975(00)00226-7
- ↑ Dasgupta, Sanjoy (1999), "Learning polytrees", in Proc. 15th Conference on Uncertainty in Artificial Intelligence (UAI 1999), Stockholm, Sweden, July-August 1999, pp. 134–141, http://cseweb.ucsd.edu/~dasgupta/papers/poly.pdf.
- ↑ de Fraysseix, Hubert; de Mendez, Patrice Ossona (1995), "Bipolar orientations revisited", Discrete Applied Mathematics 56 (2–3): 157–179, doi:10.1016/0166-218X(94)00085-R.
- ↑ Ghouila-Houri, Alain (1962), "Caractérisation des graphes non orientés dont on peut orienter les arrêtes de manière à obtenir le graphe d'une relation d'ordre", Les Comptes rendus de l'Académie des sciences 254: 1370–1371.
 |  |
