Airy zeta function
In mathematics, the Airy zeta function, studied by (Crandall 1996), is a function analogous to the Riemann zeta function and related to the zeros of the Airy function.
Definition
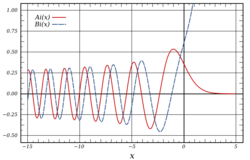
The Airy function
- [math]\displaystyle{ \mathrm{Ai}(x) = \frac{1}{\pi} \int_0^\infty \cos\left(\tfrac13t^3 + xt\right)\, dt, }[/math]
is positive for positive x, but oscillates for negative values of x. The Airy zeros are the values [math]\displaystyle{ \{a_i\}_{i=1}^\infty }[/math] at which [math]\displaystyle{ \text{Ai}(a_i) = 0 }[/math], ordered by increasing magnitude: [math]\displaystyle{ |a_1|\lt |a_2|\lt \cdots }[/math] .
The Airy zeta function is the function defined from this sequence of zeros by the series
- [math]\displaystyle{ \zeta_{\mathrm{Ai}}(s)=\sum_{i=1}^{\infty} \frac{1}{|a_i|^s}. }[/math]
This series converges when the real part of s is greater than 3/2, and may be extended by analytic continuation to other values of s.
Evaluation at integers
Like the Riemann zeta function, whose value [math]\displaystyle{ \zeta(2)=\pi^2/6 }[/math] is the solution to the Basel problem, the Airy zeta function may be exactly evaluated at s = 2:
- [math]\displaystyle{ \zeta_{\mathrm{Ai}}(2)=\sum_{i=1}^{\infty} \frac{1}{a_i^2}=\frac{3^{5/3}\Gamma^4(\frac23)}{4\pi^2}, }[/math]
where [math]\displaystyle{ \Gamma }[/math] is the gamma function, a continuous variant of the factorial. Similar evaluations are also possible for larger integer values of s.
It is conjectured that the analytic continuation of the Airy zeta function evaluates at 1 to
- [math]\displaystyle{ \zeta_{\mathrm{Ai}}(1)=-\frac{\Gamma(\frac23)}{\Gamma(\frac43)\sqrt[3]{9}}. }[/math]
References
- Crandall, Richard E. (1996), "On the quantum zeta function", Journal of Physics A: Mathematical and General 29 (21): 6795–6816, doi:10.1088/0305-4470/29/21/014, ISSN 0305-4470, Bibcode: 1996JPhA...29.6795C
External links
 |