Alpha max plus beta min algorithm

Short description: High-speed approximation of the square root of the sum of two squares

The locus of points that give the same value in the algorithm, for different values of alpha and beta

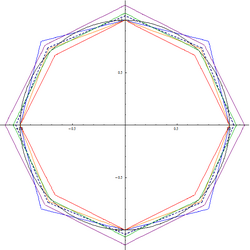
The alpha max plus beta min algorithm is a high-speed approximation of the square root of the sum of two squares. The square root of the sum of two squares, also known as Pythagorean addition, is a useful function, because it finds the hypotenuse of a right triangle given the two side lengths, the norm of a 2-D vector, or the magnitude [math]\displaystyle{ |z| = \sqrt{a^2 + b^2} }[/math] of a complex number z = a + bi given the real and imaginary parts.

The algorithm avoids performing the square and square-root operations, instead using simple operations such as comparison, multiplication, and addition. Some choices of the α and β parameters of the algorithm allow the multiplication operation to be reduced to a simple shift of binary digits that is particularly well suited to implementation in high-speed digital circuitry.

The approximation is expressed as [math]\displaystyle{ |z| = \alpha\,\mathbf{Max} + \beta\,\mathbf{Min}, }[/math] where [math]\displaystyle{ \mathbf{Max} }[/math] is the maximum absolute value of a and b, and [math]\displaystyle{ \mathbf{Min} }[/math] is the minimum absolute value of a and b.

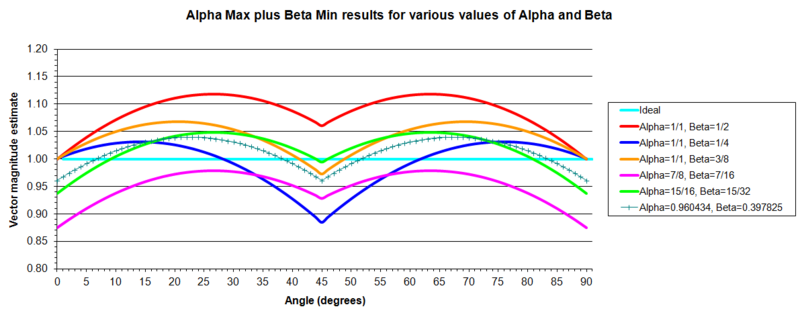
For the closest approximation, the optimum values for [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are [math]\displaystyle{ \alpha_0 = \frac{2 \cos \frac{\pi}{8}}{1 + \cos \frac{\pi}{8}} = 0.960433870103... }[/math] and [math]\displaystyle{ \beta_0 = \frac{2 \sin \frac{\pi}{8}}{1 + \cos \frac{\pi}{8}} = 0.397824734759... }[/math], giving a maximum error of 3.96%.

[math]\displaystyle{ \alpha\,\! }[/math]	[math]\displaystyle{ \beta\,\! }[/math]	Largest error (%)	Mean error (%)
1/1	1/2	11.80	8.68
1/1	1/4	11.61	3.20
1/1	3/8	6.80	4.25
7/8	7/16	12.50	4.91
15/16	15/32	6.25	3.08
[math]\displaystyle{ \alpha_0 }[/math]	[math]\displaystyle{ \beta_0 }[/math]	3.96	2.41

Improvements

When [math]\displaystyle{ \alpha \lt 1 }[/math], [math]\displaystyle{ |z| }[/math] becomes smaller than [math]\displaystyle{ \mathbf{Max} }[/math] (which is geometrically impossible) near the axes where [math]\displaystyle{ \mathbf{Min} }[/math] is near 0. This can be remedied by replacing the result with [math]\displaystyle{ \mathbf{Max} }[/math] whenever that is greater, essentially splitting the line into two different segments.

[math]\displaystyle{ |z| = \max(\mathbf{Max}, \alpha\,\mathbf{Max} + \beta\,\mathbf{Min}). }[/math]

Depending on the hardware, this improvement can be almost free.

Using this improvement changes which parameter values are optimal, because they no longer need a close match for the entire interval. A lower [math]\displaystyle{ \alpha }[/math] and higher [math]\displaystyle{ \beta }[/math] can therefore increase precision further.

Increasing precision: When splitting the line in two like this one could improve precision even more by replacing the first segment by a better estimate than [math]\displaystyle{ \mathbf{Max} }[/math], and adjust [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] accordingly.

[math]\displaystyle{ |z| = \max\big(|z_0|, |z_1|\big), }[/math]

[math]\displaystyle{ |z_0| = \alpha_0\,\mathbf{Max} + \beta_0\,\mathbf{Min}, }[/math]

[math]\displaystyle{ |z_1| = \alpha_1\,\mathbf{Max} + \beta_1\,\mathbf{Min}. }[/math]

[math]\displaystyle{ \alpha_0 }[/math]	[math]\displaystyle{ \beta_0 }[/math]	[math]\displaystyle{ \alpha_1 }[/math]	[math]\displaystyle{ \beta_1 }[/math]	Largest error (%)
1	0	7/8	17/32	−2.65%
1	0	29/32	61/128	+2.4%
1	0	0.898204193266868	0.485968200201465	±2.12%
1	1/8	7/8	33/64	−1.7%
1	5/32	27/32	71/128	1.22%
127/128	3/16	27/32	71/128	−1.13%

Beware however, that a non-zero [math]\displaystyle{ \beta_0 }[/math] would require at least one extra addition and some bit-shifts (or a multiplication), probably nearly doubling the cost and, depending on the hardware, possibly defeat the purpose of using an approximation in the first place.

See also

• Hypot, a precise function or algorithm that is also safe against overflow and underflow.

References

• Lyons, Richard G. Understanding Digital Signal Processing, section 13.2. Prentice Hall, 2004 ISBN:0-13-108989-7.
• Griffin, Grant. DSP Trick: Magnitude Estimator.

External links

• "Extension to three dimensions". Stack Exchange. May 14, 2015. https://math.stackexchange.com/q/1282435.