Angular velocity tensor
The angular velocity tensor is a skew-symmetric matrix defined by:
- [math]\displaystyle{ \Omega = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \\ \end{pmatrix} }[/math]
The scalar elements above correspond to the angular velocity vector components [math]\displaystyle{ \boldsymbol\omega=(\omega_x,\omega_y,\omega_z) }[/math].
This is an infinitesimal rotation matrix. The linear mapping Ω acts as a cross product [math]\displaystyle{ (\boldsymbol\omega \times) }[/math]:
- [math]\displaystyle{ \boldsymbol\omega \times \boldsymbol{r} = \Omega \boldsymbol{r} }[/math]
where [math]\displaystyle{ \boldsymbol{r} }[/math] is a position vector.
When multiplied by a time difference, it results in the angular displacement tensor.
Calculation of angular velocity tensor of a rotating frame
A vector [math]\displaystyle{ \mathbf r }[/math] undergoing uniform circular motion around a fixed axis satisfies:
- [math]\displaystyle{ \frac {d \mathbf r} {dt} = \boldsymbol{\omega} \times\mathbf{r} = \Omega \mathbf{r} }[/math]
Let [math]\displaystyle{ A(t) = [ \mathbf{e}_1(t) \ \mathbf{e}_2(t) \ \mathbf{e}_3(t)] }[/math] be the orientation matrix of a frame, whose columns [math]\displaystyle{ \mathbf e_1 }[/math], [math]\displaystyle{ \mathbf e_2 }[/math], and [math]\displaystyle{ \mathbf e_3 }[/math] are the moving orthonormal coordinate vectors of the frame. We can obtain the angular velocity tensor Ω(t) of A(t) as follows:
The angular velocity [math]\displaystyle{ \omega }[/math] must be the same for each of the column vectors [math]\displaystyle{ \mathbf e_i }[/math], so we have:
[math]\displaystyle{ \begin{aligned} \frac {dA}{dt} &= \begin{bmatrix} \dfrac{d\mathbf{e}_1}{dt} & \dfrac{d\mathbf{e}_2}{dt} & \dfrac{d\mathbf{e}_3}{dt} \end{bmatrix} \\ &= \begin{bmatrix} \omega \times \mathbf{e}_1 & \omega \times \mathbf{e}_2 & \omega \times \mathbf{e}_3 \end{bmatrix} \\ &= \begin{bmatrix} \Omega \mathbf{e}_1 & \Omega\mathbf{e}_2 & \Omega \mathbf{e}_3 \end{bmatrix} \\ &= \Omega A, \end{aligned} }[/math]
which holds even if A(t) does not rotate uniformly. Therefore, the angular velocity tensor is:
- [math]\displaystyle{ \Omega = \frac {dA} {dt} A^{-1} = \frac {dA} {dt} A^{\mathsf{T}}, }[/math]
since the inverse of an orthogonal matrix [math]\displaystyle{ A }[/math] is its transpose [math]\displaystyle{ A^{\mathsf{T}} }[/math].
Properties
In general, the angular velocity in an n-dimensional space is the time derivative of the angular displacement tensor, which is a second rank skew-symmetric tensor.
This tensor Ω will have n(n−1)/2 independent components, which is the dimension of the Lie algebra of the Lie group of rotations of an n-dimensional inner product space.[1]
Duality with respect to the velocity vector
In three dimensions, angular velocity can be represented by a pseudovector because second rank tensors are dual to pseudovectors in three dimensions. Since the angular velocity tensor Ω = Ω(t) is a skew-symmetric matrix:
- [math]\displaystyle{ \Omega = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0\\ \end{pmatrix}, }[/math]
its Hodge dual is a vector, which is precisely the previous angular velocity vector [math]\displaystyle{ \boldsymbol\omega=[\omega_x,\omega_y,\omega_z] }[/math].
Exponential of Ω
If we know an initial frame A(0) and we are given a constant angular velocity tensor Ω, we can obtain A(t) for any given t. Recall the matrix differential equation:
- [math]\displaystyle{ \frac {dA} {dt} = \Omega \cdot A . }[/math]
This equation can be integrated to give:
- [math]\displaystyle{ A(t) = e^{Wt}A(0) , }[/math]
which shows a connection with the Lie group of rotations.
Ω is skew-symmetric
We prove that angular velocity tensor is skew symmetric, i.e. [math]\displaystyle{ \Omega = \frac {dA(t)}{dt} \cdot A^\text{T} }[/math] satisfies [math]\displaystyle{ \Omega^\text{T} = -\Omega }[/math].
A rotation matrix A is orthogonal, inverse to its transpose, so we have [math]\displaystyle{ I=A\cdot A^\text{T} }[/math]. For [math]\displaystyle{ A=A(t) }[/math] a frame matrix, taking the time derivative of the equation gives:
- [math]\displaystyle{ 0=\frac{dA}{dt}A^\text{T}+A\frac{dA^\text{T}}{dt} }[/math]
Applying the formula [math]\displaystyle{ (A B)^\text{T}=B^\text{T}A^\text{T} }[/math],
- [math]\displaystyle{ 0 = \frac{dA}{dt}A^\text{T}+\left(\frac{dA}{dt} A^\text{T}\right)^\text{T} = \Omega + \Omega^\text{T} }[/math]
Thus, Ω is the negative of its transpose, which implies it is skew symmetric.
Coordinate-free description
At any instant [math]\displaystyle{ t }[/math], the angular velocity tensor represents a linear map between the position vector [math]\displaystyle{ \mathbf{r}(t) }[/math] and the velocity vectors [math]\displaystyle{ \mathbf{v}(t) }[/math] of a point on a rigid body rotating around the origin:
- [math]\displaystyle{ \mathbf{v} = \Omega\mathbf{r} . }[/math]
The relation between this linear map and the angular velocity pseudovector [math]\displaystyle{ \boldsymbol\omega }[/math] is the following.
Because Ω is the derivative of an orthogonal transformation, the bilinear form
- [math]\displaystyle{ B(\mathbf{r},\mathbf{s}) = (\Omega\mathbf{r}) \cdot \mathbf{s} }[/math]
is skew-symmetric. Thus we can apply the fact of exterior algebra that there is a unique linear form [math]\displaystyle{ L }[/math] on [math]\displaystyle{ \Lambda^2 V }[/math] that
- [math]\displaystyle{ L(\mathbf{r}\wedge \mathbf{s}) = B(\mathbf{r},\mathbf{s}) }[/math]
where [math]\displaystyle{ \mathbf{r}\wedge \mathbf{s} \in \Lambda^2 V }[/math] is the exterior product of [math]\displaystyle{ \mathbf{r} }[/math] and [math]\displaystyle{ \mathbf{s} }[/math].
Taking the sharp L♯ of L we get
- [math]\displaystyle{ (\Omega\mathbf{r})\cdot \mathbf{s} = L^\sharp \cdot (\mathbf{r}\wedge \mathbf{s}) }[/math]
Introducing [math]\displaystyle{ \boldsymbol\omega := {\star} (L^\sharp) }[/math], as the Hodge dual of L♯, and applying the definition of the Hodge dual twice supposing that the preferred unit 3-vector is [math]\displaystyle{ \star 1 }[/math]
- [math]\displaystyle{ (\Omega\mathbf{r}) \cdot \mathbf{s} = {\star} ( {\star} ( L^\sharp ) \wedge \mathbf{r} \wedge \mathbf{s}) = {\star} (\boldsymbol\omega \wedge \mathbf{r} \wedge \mathbf{s}) = {\star} (\boldsymbol\omega \wedge \mathbf{r} ) \cdot \mathbf{s} = (\boldsymbol\omega \times \mathbf{r} ) \cdot \mathbf{s} , }[/math]
where
- [math]\displaystyle{ \boldsymbol\omega \times \mathbf{r} := {\star} (\boldsymbol\omega \wedge \mathbf{r}) }[/math]
by definition.
Because [math]\displaystyle{ \mathbf{s} }[/math] is an arbitrary vector, from nondegeneracy of scalar product follows
- [math]\displaystyle{ \Omega\mathbf{r} = \boldsymbol\omega \times \mathbf{r} }[/math]
Angular velocity as a vector field
Since the spin angular velocity tensor of a rigid body (in its rest frame) is a linear transformation that maps positions to velocities (within the rigid body), it can be regarded as a constant vector field. In particular, the spin angular velocity is a Killing vector field belonging to an element of the Lie algebra SO(3) of the 3-dimensional rotation group SO(3).
Also, it can be shown that the spin angular velocity vector field is exactly half of the curl of the linear velocity vector field v(r) of the rigid body. In symbols,
- [math]\displaystyle{ \boldsymbol{\omega} = \frac{1}{2} \nabla\times\mathbf{v} }[/math]
Rigid body considerations
The same equations for the angular speed can be obtained reasoning over a rotating rigid body. Here is not assumed that the rigid body rotates around the origin. Instead, it can be supposed rotating around an arbitrary point that is moving with a linear velocity V(t) in each instant.
To obtain the equations, it is convenient to imagine a rigid body attached to the frames and consider a coordinate system that is fixed with respect to the rigid body. Then we will study the coordinate transformations between this coordinate and the fixed laboratory frame.
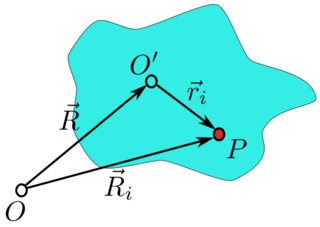
As shown in the figure on the right, the lab system's origin is at point O, the rigid body system origin is at O′ and the vector from O to O′ is R. A particle (i) in the rigid body is located at point P and the vector position of this particle is Ri in the lab frame, and at position ri in the body frame. It is seen that the position of the particle can be written:
- [math]\displaystyle{ \mathbf{R}_i=\mathbf{R}+\mathbf{r}_i }[/math]
The defining characteristic of a rigid body is that the distance between any two points in a rigid body is unchanging in time. This means that the length of the vector [math]\displaystyle{ \mathbf{r}_i }[/math] is unchanging. By Euler's rotation theorem, we may replace the vector [math]\displaystyle{ \mathbf{r}_i }[/math] with [math]\displaystyle{ \mathcal{R}\mathbf{r}_{io} }[/math] where [math]\displaystyle{ \mathcal{R} }[/math] is a 3×3 rotation matrix and [math]\displaystyle{ \mathbf{r}_{io} }[/math] is the position of the particle at some fixed point in time, say t = 0. This replacement is useful, because now it is only the rotation matrix [math]\displaystyle{ \mathcal{R} }[/math] that is changing in time and not the reference vector [math]\displaystyle{ \mathbf{r}_{io} }[/math], as the rigid body rotates about point O′. Also, since the three columns of the rotation matrix represent the three versors of a reference frame rotating together with the rigid body, any rotation about any axis becomes now visible, while the vector [math]\displaystyle{ \mathbf{r}_i }[/math] would not rotate if the rotation axis were parallel to it, and hence it would only describe a rotation about an axis perpendicular to it (i.e., it would not see the component of the angular velocity pseudovector parallel to it, and would only allow the computation of the component perpendicular to it). The position of the particle is now written as:
- [math]\displaystyle{ \mathbf{R}_i=\mathbf{R}+\mathcal{R}\mathbf{r}_{io} }[/math]
Taking the time derivative yields the velocity of the particle:
- [math]\displaystyle{ \mathbf{V}_i=\mathbf{V}+\frac{d\mathcal{R}}{dt}\mathbf{r}_{io} }[/math]
where Vi is the velocity of the particle (in the lab frame) and V is the velocity of O′ (the origin of the rigid body frame). Since [math]\displaystyle{ \mathcal{R} }[/math] is a rotation matrix its inverse is its transpose. So we substitute [math]\displaystyle{ \mathcal{I}=\mathcal{R}^\text{T}\mathcal{R} }[/math]:
- [math]\displaystyle{ \mathbf{V}_i = \mathbf{V}+\frac{d\mathcal{R}}{dt}\mathcal{I}\mathbf{r}_{io} }[/math]
- [math]\displaystyle{ \mathbf{V}_i = \mathbf{V}+\frac{d\mathcal{R}}{dt}\mathcal{R}^\text{T}\mathcal{R}\mathbf{r}_{io} }[/math]
- [math]\displaystyle{ \mathbf{V}_i = \mathbf{V}+\frac{d\mathcal{R}}{dt}\mathcal{R}^\text{T}\mathbf{r}_{i} }[/math]
or
- [math]\displaystyle{ \mathbf{V}_i = \mathbf{V}+\Omega\mathbf{r}_{i} }[/math]
where [math]\displaystyle{ \Omega = \frac{d\mathcal{R}}{dt}\mathcal{R}^\text{T} }[/math] is the previous angular velocity tensor.
It can be proved that this is a skew symmetric matrix, so we can take its dual to get a 3 dimensional pseudovector that is precisely the previous angular velocity vector [math]\displaystyle{ \boldsymbol \omega }[/math]:
- [math]\displaystyle{ \boldsymbol\omega=[\omega_x,\omega_y,\omega_z] }[/math]
Substituting ω for Ω into the above velocity expression, and replacing matrix multiplication by an equivalent cross product:
- [math]\displaystyle{ \mathbf{V}_i=\mathbf{V}+\boldsymbol\omega\times\mathbf{r}_i }[/math]
It can be seen that the velocity of a point in a rigid body can be divided into two terms – the velocity of a reference point fixed in the rigid body plus the cross product term involving the orbital angular velocity of the particle with respect to the reference point. This angular velocity is what physicists call the "spin angular velocity" of the rigid body, as opposed to the orbital angular velocity of the reference point O′ about the origin O.
Consistency
We have supposed that the rigid body rotates around an arbitrary point. We should prove that the spin angular velocity previously defined is independent of the choice of origin, which means that the spin angular velocity is an intrinsic property of the spinning rigid body. (Note the marked contrast of this with the orbital angular velocity of a point particle, which certainly does depend on the choice of origin.)
right|320 px| thumb| Proving the independence of spin angular velocity from choice of origin
See the graph to the right: The origin of lab frame is O, while O1 and O2 are two fixed points on the rigid body, whose velocity is [math]\displaystyle{ \mathbf{v}_1 }[/math] and [math]\displaystyle{ \mathbf{v}_2 }[/math] respectively. Suppose the angular velocity with respect to O1 and O2 is [math]\displaystyle{ \boldsymbol{\omega}_1 }[/math] and [math]\displaystyle{ \boldsymbol{\omega}_2 }[/math] respectively. Since point P and O2 have only one velocity,
- [math]\displaystyle{ \mathbf{v}_1 + \boldsymbol{\omega}_1\times\mathbf{r}_1 = \mathbf{v}_2 + \boldsymbol{\omega}_2\times\mathbf{r}_2 }[/math]
- [math]\displaystyle{ \mathbf{v}_2 = \mathbf{v}_1 + \boldsymbol{\omega}_1\times\mathbf{r} = \mathbf{v}_1 + \boldsymbol{\omega}_1\times (\mathbf{r}_1 - \mathbf{r}_2) }[/math]
The above two yields that
- [math]\displaystyle{ (\boldsymbol{\omega}_2-\boldsymbol{\omega}_1) \times \mathbf{r}_2=0 }[/math]
Since the point P (and thus [math]\displaystyle{ \mathbf{r}_2 }[/math]) is arbitrary, it follows that
- [math]\displaystyle{ \boldsymbol{\omega}_1 = \boldsymbol{\omega}_2 }[/math]
If the reference point is the instantaneous axis of rotation the expression of the velocity of a point in the rigid body will have just the angular velocity term. This is because the velocity of the instantaneous axis of rotation is zero. An example of the instantaneous axis of rotation is the hinge of a door. Another example is the point of contact of a purely rolling spherical (or, more generally, convex) rigid body.
References
- ↑ Rotations and Angular Momentum on the Classical Mechanics page of the website of John Baez, especially Questions 1 and 2.
 |