Ant on a rubber rope

Short description: Mathematics problem

The ant on a rubber rope is a mathematical puzzle with a solution that appears counterintuitive or paradoxical. It is sometimes given as a worm, or inchworm, on a rubber or elastic band, but the principles of the puzzle remain the same.

The details of the puzzle can vary, but a typical form is as follows:

An ant starts to crawl along a taut rubber rope 1 km long at a speed of 1 cm per second (relative to the rubber it is crawling on). At the same time, the rope starts to stretch uniformly at a constant rate of 1 km per second, so that after 1 second it is 2 km long, after 2 seconds it is 3 km long, etc. Will the ant ever reach the end of the rope?

At first consideration it seems that the ant will never reach the end of the rope, but whatever the length of the rope and the speeds, provided that the length and speeds remain steady, the ant will always be able to reach the end given sufficient time — in the form stated above, it would take 8.9×10⁴³⁴²¹ years. There are two key principles: first, since the rubber rope is stretching both in front of and behind the ant, the proportion of the rope the ant has already walked is conserved, and, second, the proportional speed of the ant is inversely proportional to the length of the rubber rope, so the distance the ant can travel is unbounded like the harmonic series.

A formal statement of the problem

For sake of analysis, the following is a formalized version of the puzzle.

Consider an ideal elastic rope on the [math]\displaystyle{ x }[/math]-axis such that at time [math]\displaystyle{ t }[/math] its endpoints are at [math]\displaystyle{ x=0 }[/math] (the starting point) and [math]\displaystyle{ x=c+vt }[/math] (the target point) for constants [math]\displaystyle{ c\gt 0 }[/math] and [math]\displaystyle{ v\gt 0 }[/math]. This is to say that at [math]\displaystyle{ t=0 }[/math] the target point is at the position [math]\displaystyle{ x=c }[/math] and that as [math]\displaystyle{ t }[/math] varies the target point moves at constant velocity [math]\displaystyle{ v }[/math]. A point object (the ant) is on the rope, and at [math]\displaystyle{ t=0 }[/math] it begins at the starting point, moving along the rope at constant velocity [math]\displaystyle{ \alpha\gt 0 }[/math] relative to the rope at its current position. Is there a time [math]\displaystyle{ t }[/math] at which the ant meets the target point?

The statement of the puzzle from the introduction corresponds to when [math]\displaystyle{ c }[/math] is 1 km, [math]\displaystyle{ v }[/math] is 1 km/s, and [math]\displaystyle{ \alpha }[/math] is 1 cm/s.

Solutions to the problem

A discrete mathematics solution

Although solving the problem appears to require analytical techniques, it can actually be answered by a combinatorial argument by considering a variation in which the rope stretches suddenly and instantaneously each second rather than stretching continuously. Indeed, the problem is sometimes stated in these terms, and the following argument is a generalisation of one set out by Martin Gardner, originally in Scientific American and later reprinted.

Consider a variation in which the rope stretches suddenly and instantaneously before each second, so that the target-point moves from [math]\displaystyle{ x=c }[/math] to [math]\displaystyle{ x=c+v }[/math] at time [math]\displaystyle{ t=0 }[/math], and from [math]\displaystyle{ x=c+v }[/math] to [math]\displaystyle{ x=c+2v }[/math] at time [math]\displaystyle{ t=1 }[/math], etc. Many versions of the problem have the rope stretch at the end of each second, but by having the rope stretch before each second we have disadvantaged the ant in its goal, so we can be sure that if the ant can reach the target point in this variation then it certainly can in the original problem, or indeed in variants where the rope stretches at the end of each second.

Let [math]\displaystyle{ \theta(t) }[/math] be the proportion of the distance from the starting-point to the target point which the ant has covered at time t. So [math]\displaystyle{ \theta(0)=0 }[/math]. In the first second the ant travels distance [math]\displaystyle{ \alpha }[/math], which is [math]\displaystyle{ \frac{\alpha}{c+v} }[/math] of the distance from the starting-point to the target-point (which is [math]\displaystyle{ c+v }[/math] throughout the first second). When the rope stretches suddenly and instantaneously, [math]\displaystyle{ \theta(t) }[/math] remains unchanged, because the ant moves along with the rubber where it is at that moment. So [math]\displaystyle{ \theta(1)=\frac{\alpha}{c+v} }[/math]. In the next second the ant travels distance [math]\displaystyle{ \alpha }[/math] again, which is [math]\displaystyle{ \frac{\alpha}{c+2v} }[/math] of the distance from the starting-point to the target-point (which is [math]\displaystyle{ c+2v }[/math] throughout that second). So [math]\displaystyle{ \theta(2)=\frac{\alpha}{c+v}+\frac{\alpha}{c+2v} }[/math]. Similarly, for any [math]\displaystyle{ n\in\mathbb{N} }[/math], [math]\displaystyle{ \theta(n)=\frac{\alpha}{c+v}+\frac{\alpha}{c+2v}+\cdots+\frac{\alpha}{c+nv} }[/math].

Notice that for any [math]\displaystyle{ k\in\mathbb{N} }[/math], [math]\displaystyle{ \frac{\alpha}{c+kv}\geqslant\frac{\alpha}{kc+kv}=\left(\frac{\alpha}{c+v}\right)\left(\frac{1}{k}\right) }[/math], so we can write [math]\displaystyle{ \theta(n)\geqslant\left(\frac{\alpha}{c+v}\right)\left(1+\frac{1}{2}+\cdots+\frac{1}{n}\right) }[/math].

The term [math]\displaystyle{ \left(1+\frac{1}{2}+\cdots+\frac{1}{n}\right) }[/math] is a partial harmonic series, which diverges, so we can find [math]\displaystyle{ N\in\mathbb{N} }[/math] such that [math]\displaystyle{ 1+\frac{1}{2}+\cdots+\frac{1}{N}\geqslant\frac{c+v}{\alpha} }[/math], which means that [math]\displaystyle{ \theta(N)\geqslant1 }[/math].

Therefore, given sufficient time, the ant will complete the journey to the target point. This solution could be used to obtain an upper bound for the time required, but does not give an exact answer for the time it will take.

An analytical solution

Absolute position x vs time t graph of the animation above: an ant crawls at 1 cm/s (red) relative to and along an elastic rope initially 4 cm long, stretching at 2 cm/s, painted in eights (shaded background). The asymptote (dashed purple) shows the position of the ant if the rope were not stretching. As the ant's position has an exponential component, it eventually catches up with the end of the rope (green) regardless of the ratio of their initial speeds. The boundaries between the background stripes can be visualised as trajectories that the ant would take should it suddenly stop when its reaches the stripe. However, since the ant is crawling, it traverses the stripes until it reaches the final one at the end.

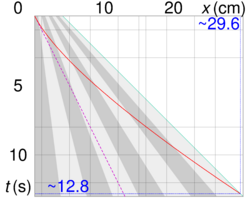
A key observation is that the speed of the ant at a given time [math]\displaystyle{ t\gt 0 }[/math] is its speed relative to the rope, i.e. [math]\displaystyle{ \alpha }[/math], plus the speed of the rope at the point where the ant is. The target-point moves with speed [math]\displaystyle{ v }[/math], so at time [math]\displaystyle{ t }[/math] it is at [math]\displaystyle{ x=c+vt }[/math]. Other points along the rope move with proportional speed, so at time [math]\displaystyle{ t }[/math] the point on the rope at [math]\displaystyle{ x=X }[/math] is moving with speed [math]\displaystyle{ \frac{vX}{c+vt} }[/math]. So if we write the position of the ant at time [math]\displaystyle{ t }[/math] as [math]\displaystyle{ y(t) }[/math], and the speed of the ant at time [math]\displaystyle{ t }[/math] as [math]\displaystyle{ y'(t) }[/math], we can write:

[math]\displaystyle{ y'(t)=\alpha+\frac{v\,y(t)}{c+vt} }[/math]

This is a first order linear differential equation, and it can be solved with standard methods. However, to do so requires some moderately advanced calculus. A much simpler approach considers the ant's position as a proportion of the distance from the starting-point to the target-point.

Consider coordinates [math]\displaystyle{ \psi }[/math] measured along the rope with the starting-point at [math]\displaystyle{ \psi=0 }[/math] and the target-point at [math]\displaystyle{ \psi=1 }[/math]. In these coordinates, all points on the rope remain at a fixed position (in terms of [math]\displaystyle{ \psi }[/math]) as the rope stretches. At time [math]\displaystyle{ t\geqslant0 }[/math], a point at [math]\displaystyle{ x=X }[/math] is at [math]\displaystyle{ \psi=\frac{X}{c+vt} }[/math], and a speed of [math]\displaystyle{ \alpha }[/math] relative to the rope in terms of [math]\displaystyle{ x }[/math], is equivalent to a speed [math]\displaystyle{ \frac{\alpha}{c+vt} }[/math] in terms of [math]\displaystyle{ \psi }[/math]. So if we write the position of the ant in terms of [math]\displaystyle{ \psi }[/math] at time [math]\displaystyle{ t }[/math] as [math]\displaystyle{ \phi(t) }[/math], and the speed of the ant in terms of [math]\displaystyle{ \psi }[/math] at time [math]\displaystyle{ t }[/math] as [math]\displaystyle{ \phi'(t) }[/math], we can write:

[math]\displaystyle{ \phi'(t)=\frac{\alpha}{c+vt} }[/math] [math]\displaystyle{ \therefore\phi(t)=\int{\frac{\alpha}{c+vt}\,dt}=\frac{\alpha}{v}\ln(c+vt)+\kappa }[/math] where [math]\displaystyle{ \kappa }[/math] is a constant of integration.

Now, [math]\displaystyle{ \phi(0)=0 }[/math] which gives [math]\displaystyle{ \kappa=-\frac{\alpha}{v}\ln{c} }[/math], so [math]\displaystyle{ \phi(t)=\frac{\alpha}{v}\ln{\left(\frac{c+vt}{c}\right)} }[/math].

If the ant reaches the target-point (which is at [math]\displaystyle{ \psi=1 }[/math]) at time [math]\displaystyle{ t=T }[/math], we must have [math]\displaystyle{ \phi(T)=1 }[/math] which gives us:

[math]\displaystyle{ \frac{\alpha}{v}\ln{\left(\frac{c+vT}{c}\right)}=1 }[/math]

[math]\displaystyle{ \therefore T=\frac{c}{v}\left(e^{v/\alpha}-1\right) }[/math]

and hence for the length of the rubber band when the ant catches the target point (i.e. the distance travelled by the ant): [math]\displaystyle{ y\left(T\right)=c+vT=c \times e^{v/\alpha}. }[/math]

(For the simple case of v = 0, we can consider the limit [math]\displaystyle{ \lim_{v \rightarrow 0} T(v) }[/math] and obtain the simple solution [math]\displaystyle{ T= \tfrac{c}{\alpha} }[/math].) As this gives a finite value [math]\displaystyle{ T }[/math] for all finite [math]\displaystyle{ c }[/math], [math]\displaystyle{ v }[/math], [math]\displaystyle{ \alpha }[/math] ([math]\displaystyle{ v\gt 0 }[/math], [math]\displaystyle{ \alpha\gt 0 }[/math]), this means that, given sufficient time, the ant will complete the journey to the target-point. This formula can be used to find out how much time is required.

For the problem as originally stated, [math]\displaystyle{ c=1\,\mathrm{km} }[/math], [math]\displaystyle{ v=1\,\mathrm{km}/\mathrm{s} }[/math] and [math]\displaystyle{ \alpha=1\,\mathrm{cm}/\mathrm{s} }[/math], which gives [math]\displaystyle{ T=(e^{100\,000}-1)\,\mathrm{s}\,\!\approx2.8\times10^{43\,429}\,\mathrm{s} }[/math]. This is a vast timespan, even compared to the estimated age of the universe, which is only about 4×10¹⁷ s. Furthermore, the length of the rope after such a time is similarly huge, 2.8×10⁴³⁴²⁹ km, so it is only in a mathematical sense that the ant can ever reach the end of this particular rope.

Intuition

Consider the situation from the introduction, which is a rope 1 km long being stretched 1 km/s, along which an ant walking is with a relative speed of 1 cm/s. At any moment, we can imagine putting down two marks on the rope: one at the ant's current position, and another 1 mm closer to the target point. If the ant were to stop for a moment, from its point of view the first mark is stationary, and the second mark is moving away at a constant speed of 1 mm/s or less (depending on the starting time). It is clear that the ant will be able reach this second mark — for a simple over-estimation of the time it takes, imagine that we "turn off" the force that the rope applies to the ant at the exact moment it reaches the first mark (leaving the ant to continue onward at constant velocity). With respect to the reference frame for the first mark at this moment, the ant is moving at 1 cm/s and the second mark is initially 1 mm away and moving at 1 mm/s, and the ant would still reach the mark in 1/9 s.

What we need to do is think about the ant's position as a fraction of the length of the rope. The above reasoning shows that this fraction is always increasing, but this is not yet enough. (The ant might asymptotically approach some fraction of the rope and never come close to reaching the target point.) What the reasoning also shows is that every 1/9 s, the fraction of the rope that the ant walks along is (at least as large as a number that is) inversely proportional to the current time, since the target point is moving proportionally to time, and the fraction of the rope this 1 mm interval corresponds to is inversely proportional to that.

Quantities that grow at a rate that is inversely proportional to time exhibit logarithmic growth, which grows without bound, however slowly that might be. This means the ant will, eventually, reach the target point.

If the speed at which the rope stretches increases through time, then the ant might not reach the target. For example, imagine one end of the rope is attached to a weight that is in free fall in a uniform gravitational field, with the rope applying no force to the weight (in other words, the target point's position is given by a function of the form [math]\displaystyle{ x = c+\tfrac{1}{2}at^2 }[/math]). If [math]\displaystyle{ c }[/math] is 1 m, [math]\displaystyle{ a }[/math] is 9.81 m/s², and the ant moves at 1 cm/s, then the ant won't cover even 0.71% of the length of the rope, despite the fact the ant is always making forward progress. However, if the ant moves at a speed greater than 1.41 m/s it will reach the end of the rope in finite time. Further there are scenarios where the speed of the ant is decreasing exponentially while the length of the rope is increasing exponentially and the ant will also reach the end of the rope in finite time.

See also

• Achilles and the tortoise
• Goodstein's theorem