Art gallery problem

From HandWiki
Short description: Mathematical problem

The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from the following real-world problem:

"In an art gallery, what is the minimum number of guards who together can observe the whole gallery?"

In the geometric version of the problem, the layout of the art gallery is represented by a simple polygon and each guard is represented by a point in the polygon. A set [math]\displaystyle{ S }[/math] of points is said to guard a polygon if, for every point [math]\displaystyle{ p }[/math] in the polygon, there is some [math]\displaystyle{ q\in S }[/math] such that the line segment between [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] does not leave the polygon.

The art gallery problem can be applied in several domains such as in robotics, when artificial intelligences (AI) need to execute movements depending on their surroundings. Other domains, where this problem is applied, are in image editing, lighting problems of a stage or installation of infrastructures for the warning of natural disasters.

Two dimensions

Four cameras cover this gallery.

There are numerous variations of the original problem that are also referred to as the art gallery problem. In some versions guards are restricted to the perimeter, or even to the vertices of the polygon. Some versions require only the perimeter or a subset of the perimeter to be guarded.

Solving the version in which guards must be placed on vertices and only vertices need to be guarded is equivalent to solving the dominating set problem on the visibility graph of the polygon.

Chvátal's art gallery theorem

Chvátal's art gallery theorem, named after Václav Chvátal, gives an upper bound on the minimal number of guards. It states:

"To guard a simple polygon with [math]\displaystyle{ n }[/math] vertices, [math]\displaystyle{ \left\lfloor n/3 \right\rfloor }[/math] guards are always sufficient and sometimes necessary."

History

The question about how many vertices/watchmen/guards were needed, was posed to Chvátal by Victor Klee in 1973.[1] Chvátal proved it shortly thereafter.[2] Chvátal's proof was later simplified by Steve Fisk, via a 3-coloring argument.[3] Chvátal has a more geometrical approach, whereas Fisk uses well-known results from Graph theory.

Fisk's short proof

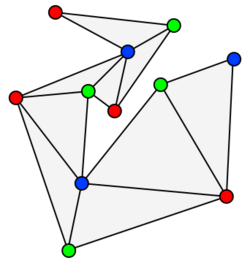
A 3-coloring of the vertices of a triangulated polygon. The blue vertices form a set of three guards, as few as is guaranteed by the art gallery theorem. However, this set is not optimal: the same polygon can be guarded by only two guards.

Steve Fisk's proof is so short and elegant that it was chosen for inclusion in Proofs from THE BOOK.[4] The proof goes as follows:

First, the polygon is triangulated (without adding extra vertices), which is possible, because the existence of triangulations is proven under certain verified conditions. The vertices of the resulting triangulation graph may be 3-colored.[lower-alpha 1] Clearly, under a 3-coloring, every triangle must have all three colors. The vertices with any one color form a valid guard set, because every triangle of the polygon is guarded by its vertex with that color. Since the three colors partition the n vertices of the polygon, the color with the fewest vertices defines a valid guard set with at most [math]\displaystyle{ \lfloor n/3\rfloor }[/math] guards.

Illustration of the proof

To illustrate the proof, we consider the polygon below. The first step is to triangulate the polygon (see Figure 1). Then, one applies a proper [math]\displaystyle{ 3 }[/math]-colouring (Figure 2) and observes that there are [math]\displaystyle{ 4 }[/math] red, [math]\displaystyle{ 4 }[/math] blue and [math]\displaystyle{ 6 }[/math] green vertices. The colour with the fewest vertices is blue or red, thus the polygon can be covered by [math]\displaystyle{ 4 }[/math] guards (Figure 3). This agrees with the art gallery theorem, because the polygon has [math]\displaystyle{ 14 }[/math] vertices, and [math]\displaystyle{ \left\lfloor \frac{14}{3} \right\rfloor = 4 }[/math].

  • Figure 1

  • Figure 2

  • Figure 3

Generalizations

Chvátal's upper bound remains valid if the restriction to guards at corners is loosened to guards at any point not exterior to the polygon.

There are a number of other generalizations and specializations of the original art-gallery theorem.[6] For instance, for orthogonal polygons, those whose edges/walls meet at right angles, only [math]\displaystyle{ \lfloor n/4 \rfloor }[/math] guards are needed. There are at least three distinct proofs of this result, none of them simple: by Kahn, Klawe, and Kleitman; by Lubiw; and by Sack and Toussaint.[7][8]

A related problem asks for the number of guards to cover the exterior of an arbitrary polygon (the "Fortress Problem"): [math]\displaystyle{ \lceil n/2 \rceil }[/math] are sometimes necessary and always sufficient if guards are placed on the boundary of the polygon, while [math]\displaystyle{ \lceil n/3 \rceil }[/math] are sometimes necessary and always sufficient if guards are placed anywhere in the exterior of the polygon.[9] In other words, the infinite exterior is more challenging to cover than the finite interior.

Computational complexity

In decision problem versions of the art gallery problem, one is given as input both a polygon and a number k, and must determine whether the polygon can be guarded with k or fewer guards. This problem is [math]\displaystyle{ \exists\mathbb{R} }[/math]-complete, as is the version where the guards are restricted to the edges of the polygon.[10] Furthermore, most of the other standard variations (such as restricting the guard locations to vertices) are NP-hard.[11]

Regarding approximation algorithms for the minimum number of guards, (Eidenbenz Stamm) proved the problem to be APX-hard, implying that it is unlikely that any approximation ratio better than some fixed constant can be achieved by a polynomial time approximation algorithm. (Ghosh 1987) showed that a logarithmic approximation may be achieved for the minimum number of vertex guards by discretizing the input polygon into convex subregions and then reducing the problem to a set cover problem. As (Valtr 1998) showed, the set system derived from an art gallery problem has bounded VC dimension, allowing the application of set cover algorithms based on ε-nets whose approximation ratio is the logarithm of the optimal number of guards rather than of the number of polygon vertices.[12] For unrestricted guards, the infinite number of potential guard positions makes the problem even more difficult. However by restricting the guards to lie on a fine grid, a more complicated logarithmic approximation algorithm can be derived under some mild extra assumptions, as shown by (Bonnet Miltzow). However, efficient algorithms are known for finding a set of at most [math]\displaystyle{ \left\lfloor n/3 \right\rfloor }[/math] vertex guards, matching Chvátal's upper bound. David Avis and Godfried Toussaint (1981) proved that a placement for these guards may be computed in O(n log n) time in the worst case, via a divide and conquer algorithm. (Kooshesh Moret) gave a linear time algorithm by using Fisk's short proof and Bernard Chazelle's linear time plane triangulation algorithm.

For simple polygons that do not contain holes, the existence of a constant factor approximation algorithm for vertex and edge guards was conjectured by Ghosh. Ghosh's conjecture was initially shown to be true for vertex guards in two special sub-classes of simple polygons, viz. monotone polygons and polygons weakly visible from an edge. (Krohn Nilsson) presented an approximation algorithm that computes in polynomial time a vertex guard set for a monotone polygon such that the size of the guard set is at most 30 times the optimal number of vertex guards. (Bhattacharya Ghosh) presented an approximation algorithm that computes in O(n2) time a vertex guard set for a simple polygon that is weakly visible from an edge such that the size of the guard set is at most 6 times the optimal number of vertex guards. Subsequently, (Bhattacharya Ghosh) claimed to have settled the conjecture completely by presenting constant factor approximation algorithms for guarding general simple polygons using vertex guards and edge guards. For vertex guarding the subclass of simple polygons that are weakly visible from an edge, a polynomial-time approximation scheme was proposed by (Ashur Filtser).

An exact algorithm was proposed by (Couto de Rezende) for vertex guards. The authors conducted extensive computational experiments with several classes of polygons showing that optimal solutions can be found in relatively small computation times even for instances associated to thousands of vertices. The input data and the optimal solutions for these instances are available for download.[13]

Three dimensions

An orthogonal polyhedron with every vertex invisible from its middle [14]
An example of a polyhedron with interior points not visible from any vertex, the figure on the right showing a cross-section through its middle, O, and parallel to ABCD

If a museum is represented in three dimensions as a polyhedron, then putting a guard at each vertex will not ensure that all of the museum is under observation. Although all of the surface of the polyhedron would be surveyed, for some polyhedra there are points in the interior that might not be under surveillance.[15]


Possible Usage Scenarios of the Art Gallery Problem

The art gallery problem can be used to position multiple cameras when the objective is to cover a large area in view of cameras, using the minimum number of cameras.

See also

Notes

  1. ↑ To prove 3-colorability of polygon triangulations, we observe that the weak dual graph to the triangulation (the undirected graph having one vertex per triangle and one edge per pair of adjacent triangles) is a tree, since any cycle in the dual graph would form the boundary of a hole in the polygon, contrary to the assumption that it has no holes. Whenever there is more than one triangle, the dual graph (like any tree) must have a vertex with only one neighbor, corresponding to a triangle that is adjacent to other triangles along only one of its sides. The smaller polygon formed by removing this triangle has a 3-coloring by mathematical induction, and this coloring is easily extended to the one additional vertex of the removed triangle.[5]

References

  1. ↑ O'Rourke (1987), p. 1.
  2. ↑ Chvátal (1975).
  3. ↑ Fisk (1978).
  4. ↑ Aigner & Ziegler (2018).
  5. ↑ O'Rourke (1987), p. 13.
  6. ↑ (Shermer 1992); (Urrutia 2000)
  7. ↑ (Kahn Klawe); (Lubiw 1985); (Sack Toussaint).
  8. ↑ O'Rourke (1987), pp. 31–80.
  9. ↑ O'Rourke (1987), pp. 146–154.
  10. ↑ Abrahamsen, Adamaszek & Miltzow (2022).
  11. ↑ (O'Rourke Supowit); (Lee Lin).
  12. ↑ Brönnimann & Goodrich (1995).
  13. ↑ (Couto de Rezende).
  14. ↑ Eryk Lipka, A note on minimal art galleries, 2019
  15. ↑ O'Rourke (1987), p. 255.

Sources



Retrieved from "https://handwiki.org/wiki/index.php?title=Art_gallery_problem&oldid=3370636"