Astronomy:Bahcall–Wolf cusp

Growth of a Bahcall–Wolf cusp. The unit of length is the black hole influence radius. The elapsed time is roughly one relaxation time. The dashed line shows the steady-state density profile.

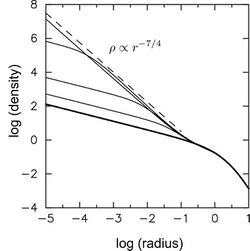
Bahcall–Wolf cusp refers to a particular distribution of stars around a massive black hole at the center of a galaxy or globular cluster. If the nucleus containing the black hole is sufficiently old, exchange of orbital energy between stars drives their distribution toward a characteristic form, such that the density of stars, ρ, varies with distance from the black hole, r, as

[math]\displaystyle{ \rho(r) \propto r^{-7/4} . }[/math]

So far, no clear example of a Bahcall–Wolf cusp has been found in any galaxy or star cluster. This may be due in part to the difficulty of resolving such a feature.

Distribution of stars around a supermassive black hole

Supermassive black holes reside in galactic nuclei. The total mass of the stars in a nucleus is roughly equal to the mass of the supermassive black hole. In the case of the Milky Way, the mass of the supermassive black hole is about 4 million Solar masses, and the number of stars in the nucleus is about ten million.

The stars move around the supermassive black hole in elliptical orbits, similar to the orbits that planets follow around the Sun. The orbital energy of a star is

[math]\displaystyle{ E = \frac{1}{2}m\boldsymbol{v}^2 - \frac{GMm}{r}, }[/math]

where m is the star's mass, v is the star's velocity, r is its distance from the supermassive black hole, and M is the supermassive black hole's mass. A star's energy remains nearly constant for many orbital periods. But after roughly one relaxation time, most of the stars in the nucleus will have exchanged energy with other stars, causing their orbits to change. Bahcall and Wolf showed that once this has taken place, the distribution of orbital energies has the form

[math]\displaystyle{ N(E)\, dE = N_0 |E|^{-9/4} dE, }[/math]

which corresponds to the density ρ=ρ₀ r ^−7/4. The figure shows how the density of stars evolves toward the Bahcall–Wolf form. The fully formed cusp extends outward to a distance of roughly one-fifth the supermassive black hole's influence radius. It is believed that relaxation times in the nuclei of small, dense galaxies are short enough for Bahcall–Wolf cusps to form. If the less massive stars dominate the total density, their density will follow the Bahcall–Wolf form, whereas the more-massive stars will follow ρ [math]\displaystyle{ \propto }[/math] r⁻².

In an old stellar population, most of the mass is either in the form of main-sequence stars, with masses [math]\displaystyle{ \lesssim }[/math] 1–2 Solar masses, or in black hole remnants, with masses ~ 10–20 Solar masses. It is likely that the main-sequence stars dominate the total density; so their density should follow the Bahcall–Wolf form whereas the black holes should have the steeper, ρ ~ r⁻² profile. On the other hand, it has been suggested that the distribution of stellar masses at the Galactic Center is "top-heavy", with a much larger fraction of black holes. If this is the case, the observed stars would be expected to attain the shallower density profile, ρ ~ r^−3/2. The number and distribution of black hole remnants at the Galactic Center is very poorly constrained.

See also

• Stellar dynamics