Astronomy:Ellis wormhole

Equatorial cross section of the Ellis wormhole, a catenoid [math]\displaystyle{ \mathcal C }[/math]

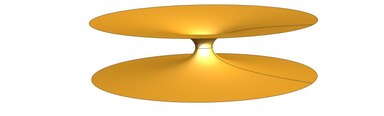
The Ellis wormhole is the special case of the Ellis drainhole in which the 'ether' is not flowing and there is no gravity. What remains is a pure traversable wormhole comprising a pair of identical twin, nonflat, three-dimensional regions joined at a two-sphere, the 'throat' of the wormhole. As seen in the image shown, two-dimensional equatorial cross sections of the wormhole are catenoidal 'collars' that are asymptotically flat far from the throat. There being no gravity in force, an inertial observer (test particle) can sit forever at rest at any point in space, but if set in motion by some disturbance will follow a geodesic of an equatorial cross section at constant speed, as would also a photon. This phenomenon shows that in space-time the curvature of space has nothing to do with gravity (the 'curvature of time’, one could say).

As a special case of the Ellis drainhole, itself a 'traversable wormhole', the Ellis wormhole dates back to the drainhole's discovery in 1969 (date of first submission) by H. G. Ellis, and independently at about the same time by K. A. Bronnikov.

Ellis and Bronnikov derived the original traversable wormhole as a solution of the Einstein vacuum field equations augmented by inclusion of a scalar field [math]\displaystyle{ \phi }[/math] minimally coupled to the geometry of space-time with coupling polarity opposite to the orthodox polarity (negative instead of positive). Some years later M. S. Morris and K. S. Thorne manufactured a duplicate of the Ellis wormhole to use as a tool for teaching general relativity, asserting that existence of such a wormhole required the presence of 'negative energy', a viewpoint Ellis had considered and explicitly refused to accept, on the grounds that arguments for it were unpersuasive.

The wormhole solution

The wormhole metric has the proper-time form

[math]\displaystyle{ c^2 d\tau^2 = c^2 dt^2 - d\sigma^2 \, , }[/math]

where

[math]\displaystyle{ \begin{align} d\sigma^2 &= d\rho^2 + r^2(\rho) \, d\Omega^2 \\ &= d\rho^2 + \left(\rho^2 + n^2\right) \, d\Omega^2 \\ &= d\rho^2 + \left(\rho^2 + n^2\right) \, \left[d\vartheta^2 + (\sin \vartheta)^2 \, d\varphi^2\right] \;\; \end{align} }[/math]

and [math]\displaystyle{ n }[/math] is the drainhole parameter that survives after the parameter [math]\displaystyle{ m }[/math] of the Ellis drainhole solution is set to 0 to stop the ether flow and thereby eliminate gravity. If one goes further and sets [math]\displaystyle{ n }[/math] to 0, the metric becomes that of Minkowski space-time, the flat space-time of the special theory of relativity.

In Minkowski space-time every timelike and every lightlike (null) geodesic is a straight 'world line' that projects onto a straight-line geodesic of an equatorial cross section of a time slice of constant [math]\displaystyle{ t, }[/math] as, for example, the one on which [math]\displaystyle{ t = 0 }[/math] and [math]\displaystyle{ \vartheta = \pi/2 }[/math], the metric of which is that of euclidean two-space in polar coordinates [math]\displaystyle{ [\rho,\varphi] }[/math], namely,

[math]\displaystyle{ ds^2 = d\rho^2 + \rho^2 \, d\varphi^2 \, . }[/math]

Every test particle or photon is seen to follow such an equatorial geodesic at a fixed coordinate speed, which could be 0, there being no gravitational field built into Minkowski space-time. These properties of Minkowski space-time all have their counterparts in the Ellis wormhole, modified, however, by the fact that the metric and therefore the geodesics of equatorial cross sections of the wormhole are not straight lines, rather are the 'straightest possible' paths in the cross sections. It is of interest, therefore, to see what these equatorial geodesics look like.

Equatorial geodesics of the wormhole

Geodesics confined to one side of the wormhole throat

Geodesics spiraling onto the wormhole throat

Geodesics passing through the wormhole throat

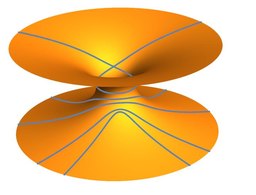
The equatorial cross section of the wormhole defined by [math]\displaystyle{ t = 0 }[/math] and [math]\displaystyle{ \vartheta = \pi/2 }[/math] (representative of all such cross sections) bears the metric

[math]\displaystyle{ ds^2 = d\rho^2 + \left(\rho^2 + n^2\right) \, d\varphi^2 \, . }[/math]

When the cross section with this metric is embedded in euclidean three-space the image is the catenoid [math]\displaystyle{ \mathcal C }[/math] shown above, with [math]\displaystyle{ \rho }[/math] measuring the distance from the central circle at the throat, of radius [math]\displaystyle{ n }[/math], along a curve on which [math]\displaystyle{ \varphi }[/math] is fixed (one such being shown). In cylindrical coordinates [math]\displaystyle{ [r,\varphi,z] }[/math] the equation [math]\displaystyle{ r = n \cosh(z/n) }[/math] has [math]\displaystyle{ \mathcal C }[/math] as its graph.

After some integrations and substitutions the equations for a geodesic of [math]\displaystyle{ \mathcal C }[/math] parametrized by [math]\displaystyle{ s }[/math] reduce to

[math]\displaystyle{ \frac{d\varphi}{ds} = \frac{h}{\rho^2 + n^2} }[/math]

and

[math]\displaystyle{ \left(\frac{d\rho}{ds}\right)^2 + \frac{h^2}{\rho^2 + n^2} \, = 1, }[/math]

where [math]\displaystyle{ h }[/math] is a constant. If [math]\displaystyle{ d\rho/ds \equiv 0 \, , }[/math] then [math]\displaystyle{ h^2 = \rho^2 + n^2 \geq n^2 \, , }[/math] [math]\displaystyle{ \textstyle d\varphi/ds = 1/h, }[/math] and [math]\displaystyle{ \textstyle \rho = \pm \sqrt{h^2 - n^2} \, , }[/math] and vice versa. Thus every 'circle of latitude' ([math]\displaystyle{ \rho = }[/math] constant) is a geodesic. If on the other hand [math]\displaystyle{ d\rho/ds }[/math] is not identically 0, then its zeroes are isolated and the reduced equations can be combined to yield the orbital equation

[math]\displaystyle{ \left(\frac{d\varphi}{d\rho}\right)^2 = \frac{h^2}{\left(\rho^2 + n^2\right)\left(\rho^2 + n^2 - h^2\right)} \, . }[/math]

There are three cases to be considered:

• [math]\displaystyle{ h^2 \gt n^2, }[/math] which implies that [math]\displaystyle{ \rho^2 \geq h^2 - n^2 \gt 0, }[/math] thus that the geodesic is confined to one side of the wormhole or the other and has a turning point at [math]\displaystyle{ \textstyle \rho = \sqrt{h^2 - n^2} }[/math] or [math]\displaystyle{ \textstyle \rho = -\sqrt{h^2 - n^2} \, ; }[/math]
• [math]\displaystyle{ h^2 = n^2, }[/math] which entails that [math]\displaystyle{ \rho^2 \gt 0, }[/math] so that the geodesic does not cross the throat at [math]\displaystyle{ \rho = 0, }[/math] but spirals onto it from one side or the other;
• [math]\displaystyle{ h^2 \lt n^2, }[/math] which allows the geodesic to traverse the wormhole from either side to the other.

The figures exhibit examples of the three types. If [math]\displaystyle{ s }[/math] is allowed to vary from [math]\displaystyle{ -\infty }[/math] to [math]\displaystyle{ \infty, }[/math] the number of orbital revolutions possible for each type, latitudes included, is unlimited. For the first and third types the number rises to infinity as [math]\displaystyle{ h^2 \to n^2; }[/math] for the spiral type and the latitudes the number is already infinite.

That these geodesics can bend around the wormhole makes clear that the curvature of space alone, without the aid of gravity, can cause test particles and photons to follow paths that deviate significantly from straight lines and can create lensing effects.

Dynamic Ellis wormhole

There is a dynamic version of the Ellis wormhole that is a solution of the same field equations that the static Ellis wormhole is a solution of. Its metric is

[math]\displaystyle{ c^2 d\tau^2 = c^2 dt^2 - d\sigma^2 \, , }[/math]

where

[math]\displaystyle{ d\sigma^2 = d\rho^2 + \left[\left(1 + a^2\right) \rho^2 + a^2 c^2 t^2 \, \right] \, d\Omega^2 \, , }[/math]

[math]\displaystyle{ a }[/math] being a positive constant. There is a 'point singularity' at [math]\displaystyle{ t = \rho = 0, }[/math] but everywhere else the metric is regular and curvatures are finite. Geodesics that do not encounter the point singularity are complete; those that do can be extended beyond it by proceeding along any of the geodesics that encounter the singularity from the opposite time direction and have compatible tangents (similarly to geodesics of the graph of [math]\displaystyle{ z = (xy)^3 }[/math] that encounter the singularity at the origin).

For a fixed nonzero value of [math]\displaystyle{ t }[/math] the equatorial cross section on which [math]\displaystyle{ \vartheta = \pi/2 }[/math] has the metric

[math]\displaystyle{ \begin{align} ds^2 &= d\rho^2 + r^2(t,\rho) \, d\varphi^2 \\ &= d\rho^2 + \left[\left(1 + a^2\right) \rho^2 + a^2 c^2 t^2 \, \right] \, d\varphi^2 \, . \end{align} }[/math]

This metric describes a 'hypercatenoid' similar to the equatorial catenoid of the static wormhole, with the radius [math]\displaystyle{ n }[/math] of the throat (where [math]\displaystyle{ \rho = 0 }[/math]) now replaced by [math]\displaystyle{ a c |t|, }[/math] and in general each circle of latitude of geodesic radius [math]\displaystyle{ \rho }[/math] having circumferential radius [math]\displaystyle{ \textstyle r(t,\rho) = \sqrt{(1 + a^2) \rho^2 + a^2 c^2 t^2} }[/math].

For [math]\displaystyle{ t = 0 }[/math] the metric of the [math]\displaystyle{ \vartheta = \pi/2 }[/math] equatorial cross section is

[math]\displaystyle{ ds^2 = d\rho^2 + \left(1 + a^2\right)\rho^2 \, d\varphi^2 \, , }[/math]

which describes a 'hypercone' with its vertex at the singular point, its latitude circles of geodesic radius [math]\displaystyle{ \rho }[/math] having circumferences [math]\displaystyle{ \textstyle 2 \pi r(0,\rho) = 2 \pi \sqrt{1 + a^2} \rho \, . }[/math] Unlike the catenoid, neither the hypercatenoid nor the hypercone is fully representable as a surface in euclidean three-space; only the portions where [math]\displaystyle{ \textstyle |dr(t,\rho)/d\rho| = (1 + a^2) |\rho|\big/\sqrt{(1 + a^2)\rho^2 + a^2 c^2 t^2} \leq 1 }[/math] (thus where [math]\displaystyle{ \textstyle |\rho| \leq c |t|\big/\sqrt{1 + a^2} }[/math] or equivalently [math]\displaystyle{ \textstyle r(t,\rho) \leq \sqrt{1 + a^2} c |t| }[/math]) can be embedded in that way.

Dynamically, as [math]\displaystyle{ t }[/math] advances from [math]\displaystyle{ -\infty }[/math] to [math]\displaystyle{ \infty }[/math] the equatorial cross sections shrink from hypercatenoids of infinite radius to hypercones (hypercatenoids of zero radius) at [math]\displaystyle{ t = 0, }[/math] then expand back to hypercatenoids of infinite radius. Examination of the curvature tensor reveals that the full dynamic Ellis wormhole space-time manifold is asymptotically flat in all directions [math]\displaystyle{ - }[/math] timelike, lightlike, and spacelike.

Applications

• Scattering by an Ellis wormhole
• Gravitational lensing in the Ellis wormhole
  • Microlensing by the Ellis wormhole
  • Wave effect in lensing by the Ellis wormhole
  • Image centroid displacements due to microlensing by the Ellis wormhole
  • Exact lens equation for the Ellis wormhole
  • Lensing by wormholes