Astronomy:Minimum mass

Short description: Lowest possible mass of the celestial object

Left: A representation of a star orbited by a planet. All the movement of the star is along the viewer's line-of-sight; Doppler spectroscopy will give a true value of the planet's mass.
Right: In this case none of the star's movement is along the viewer's line-of-sight and the Doppler spectroscopy method will not detect the planet at all.

In astronomy, minimum mass is the lower-bound calculated mass of observed objects such as planets, stars and binary systems, nebulae, and black holes.

Minimum mass is a widely cited statistic for extrasolar planets detected by the radial velocity method or Doppler spectroscopy, and is determined using the binary mass function. This method reveals planets by measuring changes in the movement of stars in the line-of-sight, so the real orbital inclinations and true masses of the planets are generally unknown. This is a result of sin i degeneracy.

If inclination i can be determined, the true mass can be obtained from the calculated minimum mass using the following relationship: [math]\displaystyle{ M_\text{true} = \frac{M_\min}{\sin i} }[/math]

Exoplanets

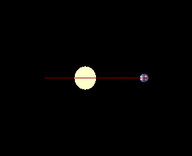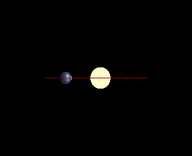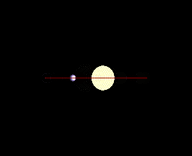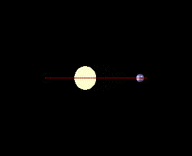
Orientation of the transit to Earth

A view of inclination that would appear flat upon the green plane from Earth.

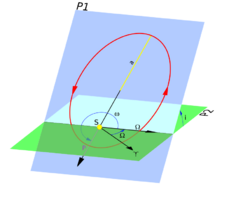
Most stars will not have their planets lined up and orientated so that they eclipse over the center of the star and give the viewer on earth a perfect transit. It is for this reason that when we often are only able to extrapolate a minimum mass when viewing a star's wobble because we do not know the inclination and therefore only be able to calculate the part pulling the star on the plane of celestial sphere.

For orbiting bodies in extrasolar planetary systems, an inclination of 0° or 180° corresponds to a face-on orbit (which cannot be observed by radial velocity), whereas an inclination of 90° corresponds to an edge-on orbit (for which the true mass equals the minimum mass).

Planets with orbits highly inclined to the line of sight from Earth produce smaller visible wobbles, and are thus more difficult to detect. One of the advantages of the radial velocity method is that eccentricity of the planet's orbit can be measured directly. One of the main disadvantages of the radial-velocity method is that it can only estimate a planet's minimum mass ([math]\displaystyle{ M_\text{true} \cdot {\sin i} }[/math]). This is called Sin i degeneracy. The posterior distribution of the inclination angle i depends on the true mass distribution of the planets.

Radial velocity method

However, when there are multiple planets in the system that orbit relatively close to each other and have sufficient mass, orbital stability analysis allows one to constrain the maximum mass of these planets. The radial velocity method can be used to confirm findings made by the transit method. When both methods are used in combination, then the planet's true mass can be estimated.

Although radial velocity of the star only gives a planet's minimum mass, if the planet's spectral lines can be distinguished from the star's spectral lines then the radial velocity of the planet itself can be found, and this gives the inclination of the planet's orbit. This enables measurement of the planet's actual mass. This also rules out false positives, and also provides data about the composition of the planet. The main issue is that such detection is possible only if the planet orbits around a relatively bright star and if the planet reflects or emits a lot of light.

The term true mass is synonymous with the term mass, but is used in astronomy to differentiate the measured mass of a planet from the minimum mass usually obtained from radial velocity techniques. Methods used to determine the true mass of a planet include measuring the distance and period of one of its satellites, advanced astrometry techniques that use the motions of other planets in the same star system, combining radial velocity techniques with transit observations (which indicate very low orbital inclinations), and combining radial velocity techniques with stellar parallax measurements (which also determine orbital inclinations).

Use of sine function

Unit circle: the radius has length 1. The variable t measures the angle referred to as θ in the text.

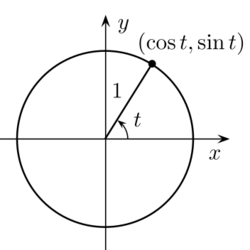
In trigonometry, a unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system.

Let a line through the origin, making an angle of θ with the positive half of the x-axis, intersect the unit circle. The x- and y-coordinates of this point of intersection are equal to cos(θ) and sin(θ), respectively. The point's distance from the origin is always 1.

Animation showing how the sine function (in red) [math]\displaystyle{ y = \sin(\theta) }[/math] is graphed from the y-coordinate (red dot) of a point on the unit circle (in green) at an angle of θ.

Stars

With a mass only 93 times that of Jupiter (|♃|J}}}}}}), or .09 M_☉, AB Doradus C, a companion to AB Doradus A, is the smallest known star undergoing nuclear fusion in its core. For stars with similar metallicity to the Sun, the theoretical minimum mass the star can have, and still undergo fusion at the core, is estimated to be about 75 M_J. When the metallicity is very low, however, a recent study of the faintest stars found that the minimum star size seems to be about 8.3% of the solar mass, or about 87 M_J. Smaller bodies are called brown dwarfs, which occupy a poorly defined grey area between stars and gas giants.