Astronomy:Phillips relationship
In astrophysics, the Phillips relationship is the relationship between the peak luminosity of a Type Ia supernova and the speed of luminosity evolution after maximum light. The relationship was independently discovered by the American statistician and astronomer Bert Woodard Rust and the Soviet astronomer Yury Pavlovich Pskovskii (ru) in the 1970s.[1][2][3] They found that the faster the supernova faded from maximum light, the fainter its peak magnitude was. As a main parameter characterizing the light curve shape, Pskovskii used β, the mean rate of decline in photographic brightness from maximum light to the point at which the luminosity decline rate changes. β is measured in magnitudes per 100-day intervals.[4] Selection of this parameter is justified by the fact that, at that time, the probability of discovering a supernova before the maximum light, and obtain the full light curve, was small. Moreover, the existing light curves were mostly incomplete. On the other hand, to determine the decline after the maximum light was rather simple for most observed supernovae.
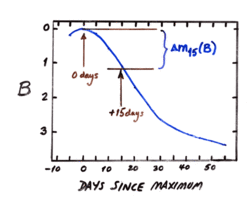
In the early 1980s CCD cameras appeared, and the number of SNe discoveries increased substantially. Moreover, the probability of discovering SNe before they reached maximum light and following their brightness evolution longer also increased. The first light curves of SNe Ia obtained using CCD photometry showed that some supernovae had faster decline rates than others. Later, the low luminosity Ia SN 1991bg with a fast decline rate was discovered. All this motivated the American astronomer Mark M. Phillips to revise this relationship precisely during the course of the Calán/Tololo Supernova Survey.[5] The correlation had been difficult to prove because Pskovskii's slope (β) parameter was difficult to measure with precision in practice, a necessary condition to prove the correlation. Rather than trying to determine the slope, Phillips used a simpler and more robust procedure that consisted in "measuring the total amount in magnitudes that the light curve decays from its peak brightness during some specified period following maximum light." It was defined as the decline in the B-magnitude light curve from maximum light to the magnitude 15 days after B-maximum, a parameter he called . The lead sentence of the acknowledgments section of Phillips' paper states: "I am indebted to George Jacoby for suggesting the parameter as an alternative to Pskovskii's β." The relation states that the maximum intrinsic B-band magnitude is given by
Phillips dedicated the journal article confirming Yuri Pskovskii's proposed correlation to Pskovskii, who died a few weeks after Phillips' evidence confirming the relationship was published.
It has been recast to include the evolution in multiple photometric bandpasses, with a significantly shallower slope[7][8] and as a stretch in the time axis relative to a standard template.[9] The relation is typically used to bring any Type Ia supernova peak magnitude to a standard candle value.
References
- ↑ Rust, B. W. The Use of Supernovae Light Curves for Testing the Expansion Hypothesis and Other Cosmological Relations (PDF) (PhD thesis). University of Illinois.
- ↑ Pskovskii, Yu. P. (1977). "Light curves, color curves, and expansion velocity of type I supernovae as functions of the rate of brightness decline". Soviet Astronomy 21: 675. Bibcode: 1977SvA....21..675P.
- ↑ Pskovskii, Yu. P. (1984). "Photometric classification and basic parameters of type I supernovae". Soviet Astronomy 28: 658–664. Bibcode: 1984SvA....28..658P.
- ↑ Pskovskii, Yu. P. (1967). "The Photometric Properties of Supernovae". Soviet Astronomy 11: 63–69. Bibcode: 1967SvA....11...63P.
- ↑ Phillips, M. M. (1993). "The absolute magnitudes of Type IA supernovae". Astrophysical Journal Letters 413 (2): L105–L108. doi:10.1086/186970. Bibcode: 1993ApJ...413L.105P.
- ↑ Rosswog, Stephan; Brüggen, Marcus (3 March 2011). High Energy Astrophysics. Cambridge University Press. ISBN 978-0521674423.
- ↑ Hamuy, Mario; Phillips, M. M.; Maza, Jose; Suntzeff, Nicholas B.; Schommer, R. A.; Aviles, R. (1995). "A Hubble Diagram of Distant Type 1a Supernovae". The Astronomical Journal 109: 1. doi:10.1086/117251. Bibcode: 1995AJ....109....1H. https://ui.adsabs.harvard.edu/abs/1995AJ....109....1H/abstract.
- ↑ Riess, Adam G.; Press, William H.; Kirshner, Robert P. (1996). "A Precise Distance Indicator: Type IA Supernova Multicolor Light-Curve Shapes". The Astrophysical Journal 473: 88. doi:10.1086/178129. Bibcode: 1996ApJ...473...88R. https://ui.adsabs.harvard.edu/abs/1996ApJ...473...88R/abstract.
- ↑ Perlmutter, S. A., et al. 1997, NATO ASIC Proc. 486: Thermonuclear Supernovae, 749
 |
