Astronomy:Spin-flip

Short description: Sudden change of spin axis caused by merging with another black hole

Schematic diagram of a black hole spin-flip.

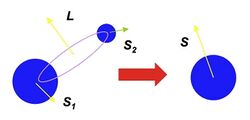
A black hole spin-flip occurs when the spin axis of a rotating black hole undergoes a sudden change in orientation due to absorption of a second (smaller) black hole. Spin-flips are believed to be a consequence of galaxy mergers, when two supermassive black holes form a bound pair at the center of the merged galaxy and coalesce after emitting gravitational waves. Spin-flips are significant astrophysically since a number of physical processes are associated with black hole spins; for instance, jets in active galaxies are believed to be launched parallel to the spin axes of supermassive black holes. A change in the rotation axis of a black hole due to a spin-flip would therefore result in a change in the direction of the jet.

Physics of spin-flips

A spin-flip is a late stage in the evolution of a binary black hole. The binary consists of two black holes, with masses [math]\displaystyle{ M_1 }[/math] and [math]\displaystyle{ M_2 }[/math], that revolve around their common center of mass. The total angular momentum [math]\displaystyle{ J }[/math] of the binary system is the sum of the angular momentum of the orbit, [math]\displaystyle{ {L} }[/math], plus the spin angular momenta [math]\displaystyle{ {S}_{1,2} = {S}_{1} + {S}_{2} }[/math] of the two holes. If we write [math]\displaystyle{ \mathbf{M_1}, \mathbf{M_2} }[/math] as the masses of each hole and [math]\displaystyle{ \mathbf{a_1}, \mathbf{a_2} }[/math] as their Kerr parameters, then use the angle from north of their spin axes as given by [math]\displaystyle{ \theta }[/math], we can write,

[math]\displaystyle{ \mathbf{S}_{1} = \{\mathbf{a}_{1} \mathbf{M}_{1} \cos(\pi/2-\theta), \mathbf{a}_{1} \mathbf{M}_{1} \sin(\tfrac \pi 2 - \theta)\} }[/math] [math]\displaystyle{ \mathbf{S}_{2} = \{\mathbf{a}_{2} \mathbf{M}_{2}\cos(\tfrac \pi 2 - \theta), \mathbf{a}_{2} \mathbf{M}_{2}\sin(\tfrac \pi 2 - \theta)\} }[/math] [math]\displaystyle{ \mathbf{J}_\text{init} = \mathbf{L}_\text{orb} + \mathbf{S}_1 + \mathbf{S}_2. }[/math]

If the orbital separation is sufficiently small, emission of energy and angular momentum in the form of gravitational radiation will cause the orbital separation to drop. Eventually, the smaller hole [math]\displaystyle{ M_2 }[/math] reaches the innermost stable circular orbit, or ISCO, around the larger hole. Once the ISCO is reached, there no longer exists a stable orbit, and the smaller hole plunges into the larger hole, coalescing with it. The final angular momentum after coalescence is just

[math]\displaystyle{ \mathbf{J}_\text{final} = \mathbf{S}, }[/math]

the spin angular momentum of the single, coalesced hole. Neglecting the angular momentum that is carried away by gravitational waves during the final plunge—which is small—conservation of angular momentum implies

[math]\displaystyle{ \mathbf{S} \approx \mathbf{L}_\text{ISCO} + \mathbf{S}_1 + \mathbf{S}_2. }[/math]

[math]\displaystyle{ S_2 }[/math] is of order [math]\displaystyle{ (M_2 / M_1)^2 }[/math] times [math]\displaystyle{ S_1 }[/math] and can be ignored if [math]\displaystyle{ M_2 }[/math] is much smaller than [math]\displaystyle{ M_1 }[/math]. Making this approximation,

[math]\displaystyle{ \mathbf{S} \approx \mathbf{L}_\text{ISCO} + \mathbf{S}_1. }[/math]

This equation states that the final spin of the hole is the sum of the larger hole's initial spin plus the orbital angular momentum of the smaller hole at the last stable orbit. Since the vectors [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ L }[/math] are generically oriented in different directions, [math]\displaystyle{ S }[/math] will point in a different direction than [math]\displaystyle{ S_1 }[/math]—a spin-flip.

The angle by which the black hole's spin re-orients itself depends on the relative size of [math]\displaystyle{ L_{\rm ISCO} }[/math] and [math]\displaystyle{ S_1 }[/math], and on the angle between them. At one extreme, if [math]\displaystyle{ S_1 }[/math] is very small, the final spin will be dominated by [math]\displaystyle{ L_{\rm ISCO} }[/math] and the flip angle can be large. At the other extreme, the larger black hole might be a maximally-rotating Kerr black hole initially. Its spin angular momentum is then of order

[math]\displaystyle{ S_1 \approx G M_1^2/c. }[/math]

The orbital angular momentum of the smaller hole at the ISCO depends on the direction of its orbit, but is of order

[math]\displaystyle{ L_\text{ISCO} \approx G M_1 M_2/c. }[/math]

Comparing these two expressions, it follows that even a fairly small hole, with mass about one-fifth that of the larger hole, can reorient the larger hole by 90 degrees or more.

Connection with radio galaxies

Black hole spin-flips were first discussed in the context of a particular class of radio galaxy, the X-shaped radio sources. The X-shaped galaxies exhibit two, misaligned pairs of radio lobes: the "active" lobes and the "wings". It is believed that the wings are oriented in the direction of the jet prior to the spin-flip, and that the active lobes point in the current jet direction. The spin-flip could have been caused by absorption of a second black hole during a galaxy merger.

See also

• Astronomy:Supermassive black hole – Largest type of black hole
• Astronomy:Gravitational wave – Propagating spacetime ripple
• Astronomy:Radio galaxy – Type of active galaxy that is very luminous at radio wavelengths

External links

• Massive black hole binary evolution An article on binary black holes.
• Scientists Detect "Smoking Gun" of Colliding Black Holes