Astronomy:Three-mirror anastigmat
A three-mirror anastigmat is an anastigmat telescope built with three curved mirrors, enabling it to minimize all three main optical aberrations – spherical aberration, coma, and astigmatism. This is primarily used to enable wide fields of view, much larger than possible with telescopes with just one or two curved surfaces.
A telescope with only one curved mirror, such as a Newtonian telescope, will always have aberrations. If the mirror is spherical, it will suffer from spherical aberration. If the mirror is made parabolic, to correct the spherical aberration, then it must necessarily suffer from coma and off-axis astigmatism. With two curved mirrors, such as the Ritchey–Chrétien telescope, coma can be minimized as well. This allows a larger useful field of view, and the remaining astigmatism is symmetrical around the distorted objects, allowing astrometry across the wide field of view. However, the astigmatism can be reduced by including a third curved optical element. When this element is a mirror, the result is a three-mirror anastigmat. In practice, the design may also include any number of flat fold mirrors, used to bend the optical path into more convenient configurations.
History
Many combinations of three mirror figures can be used to cancel all third-order aberrations. In general these involve solving a relatively complicated set of equations. A few configurations are simple enough, however, that they could be designed starting from a few intuitive concepts.
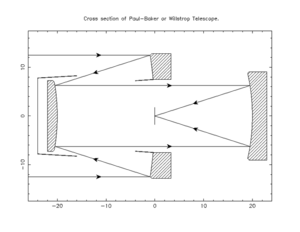
Paul telescope
The first were proposed in 1935 by Maurice Paul.[1] The basic idea behind Paul's solution is that spherical mirrors, with an aperture stop at the centre of curvature, have only spherical aberration – no coma or astigmatism (but they do produce an image on a curved surface of half the radius of curvature of the spherical mirror). So if the spherical aberration can be corrected, a very wide field of view can be obtained. This is similar to the conventional Schmidt design, but the Schmidt does this with a refractive corrector plate instead of a third mirror.
Paul's idea was to start with a Mersenne beam compressor, which looks like a Cassegrain made from two (confocal) paraboloids, with both the input and output beams collimated. The compressed input beam is then directed to a spherical tertiary mirror, which results in traditional spherical aberration. Paul's key insight is that the secondary can then be converted back to a spherical mirror.
One way to look at this is to imagine the tertiary mirror, which suffers from spherical aberration, is replaced by a Schmidt telescope, with a correcting plate at its centre of curvature. If the radii of the secondary and tertiary are of the same magnitude, but opposite sign, and if the centre of curvature of the tertiary is placed directly at the vertex of the secondary mirror, then the Schmidt plate would lie on top of the paraboloid secondary mirror. Therefore, the Schmidt plate required to make the tertiary mirror a Schmidt telescope is eliminated by the paraboloid figuring on the convex secondary of the Mersenne system, as each corrects the same magnitude of spherical aberration, but the opposite sign. Also, as the system of Mersenne + Schmidt is the sum of two anastigmats (the Mersenne system is an anastigmat, and so is the Schmidt system), the resultant system is also an anastigmat, as third-order aberrations are purely additive.[2] In addition the secondary is now easier to fabricate. This design is also called a Mersenne–Schmidt, since it uses a Mersenne configuration as the corrector for a Schmidt telescope.
Paul–Baker telescope
Paul's solution had a curved focal plane, but this was corrected in the Paul–Baker design, introduced in 1969 by James Gilbert Baker.[3] The Paul–Baker design adds extra spacing and reshapes the secondary to elliptical, which corrects field curvature to flatten the focal plane.[4]
Korsch telescope
A more general set of solutions was developed by Dietrich Korsch in 1972.[5] A Korsch telescope is corrected for spherical aberration, coma, astigmatism, and field curvature and can have a wide field of view while ensuring that there is little stray light in the focal plane.
Eisenberg-Pearson telescope
A variation of the Korsch design is the Two-Mirror three-surface telescope[6] introduced by Shai Eisenberg and Earl T. Pearson in 1987. Employing the Korsch equations with minimal modifications, the number of mirrors is reduced from three to two by combining the primary surface and the tertiary surface on the same mirror. In one option the tertiary is identical to the primary, whereas the second option shows the tertiary as polished into the primary mirror. The Eisenberg-Pearson telescope does not require a flat fold mirror to allow access to the image plane since the focal plane is located behind the secondary mirror. A compact illustration of the Korsch telescope published in 1995 by Shai Eisenberg[7] is the solid version of the design with the use of total internal reflection (TIR) to integrate the fourth fold mirror without introducing vignetting.


Examples
- The James Webb Space Telescope is a three-mirror anastigmat featuring an ellipsoidal primary, hyperboloidal secondary, and ellipsoidal tertiary.[8]
- The Euclid mission uses a Korsch telescope.
- The "Cambridge University Three-Mirror Telescope". http://www.ast.cam.ac.uk/about/three-mirror.telescope. project includes a 100 mm working model built in 1985 and a 500 mm prototype built in 1986.
- The Vera C. Rubin Observatory's telescope (formerly known as Large Synoptic Survey Telescope) is an Eisenberg-Pearson design with an additional refractive corrector.
- The KH-11 Kennen (or perhaps the now cancelled Future Imagery Architecture) telescopes may be a three-mirror anastigmat, since the spare telescopes given to NASA by the National Reconnaissance Office are of this form.
- The Extremely Large Telescope will be a three-mirror anastigmat design, with two additional flat fold mirrors.
- The Deimos‑2 and DubaiSat‑2 Earth observation satellites both carry a three-mirror anastigmat Korsch design telescope.[9][10]
- Ralph imaging spectrometer on New Horizons spacecraft
- The Nancy Grace Roman Space Telescope, formerly named the Wide Field Infrared Survey Telescope (WFIRST), employs a folded three-mirror anastigmat featuring an ellipsoidal primary, hyperboloidal secondary, and ellipsoidal tertiary. [11] An earlier design used an off-axis three-mirror anastigmat.[12]
See also
References
- ↑ Paul, Maurice (May 1935). "Systèmes correcteurs pour réflecteurs astronomiques". Revue d'Optique Théorique et Instrumentale 14 (5): 169–202.
- ↑ Wilson, R. N. (2007). Reflecting Telescope Optics I. Springer. p. 227. ISBN 978-3-540-40106-3.
- ↑ Baker, J.G. (1969). "On improving the effectiveness of large telescopes". IEEE Transactions on Aerospace and Electronic Systems AES-5 (2): 261–272. doi:10.1109/TAES.1969.309914. Bibcode: 1969ITAES...5..261B.
- ↑ Sacek, V. (14 July 2006). "Paul-Baker and other three-mirror anastigmatic aplanats". Telescope-Optics.net. http://www.telescope-optics.net/paul-baker_telescope.htm.
- ↑ Korsch, Dietrich (December 1972). "Closed form solution for three-mirror telescopes, corrected for spherical aberration, coma, astigmatism, and field curvature". Applied Optics 11 (12): 2986–2987. doi:10.1364/AO.11.002986. PMID 20119447. Bibcode: 1972ApOpt..11.2986K.
- ↑ Shai Eisenberg and Earl T. Pearson "Two- Mirror three-surface telescope"., Proc SPIE Vol. 751, p24, January 1987.
- ↑ Yeshayahu S. Eisenberg USP 5,930,055 "Lens Apparatus"
- ↑ Contreras, James W.; Lightsey, Paul A. (22 October 2004). "Optical design and analysis of the James Webb Space Telescope: Optical telescope element". Novel Optical Systems Design and Optimization VII. Conference Proceedings of the SPIE. 5524. p. 30. doi:10.1117/12.559871. Bibcode: 2004SPIE.5524...30C. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/5524/0000/Optical-design-and-analysis-of-the-James-Webb-Space-Telescope/10.1117/12.559871.full?SSO=1.
- ↑ "DEIMOS‑2: Costeffective, Very-high Resolution Multispectral Imagery". http://www.gsdi.org/gsdiconf/gsdi14/slides/4.2Deimos.pdf.
- ↑ "Technical Specifications of DubaiSat 2". http://mbrsc.ae/en/page/technical-specifications-dubaisat2.
- ↑ Pasquale, Bert A. et al. (17 September 2018). "Optical design and predicted performance of the WFIRST phase-b imaging optics assembly and wide field instrument". Current Developments in Lens Design and Optical Engineering XIX. 107450K. p. 18. doi:10.1117/12.2325859. ISBN 9781510620612. Bibcode: 2018SPIE10745E..0KP. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/10745/2325859/Optical-design-and-predicted-performance-of-the-WFIRST-phase-b/10.1117/12.2325859.full?SSO=1.
- ↑ Content, D.A.; Goullioud, R.; Lehan, J.P.; Mentzell, J.E. (14 September 2011). "Optical design trade study for the Wide Field Infrared Survey Telescope [WFIRST]". UV/Optical/IR Space Telescopes and Instruments: Innovative Technologies and Concepts V. Conference Proceedings of the SPIE. 8146. pp. 81460Y. doi:10.1117/12.898528. Bibcode: 2011SPIE.8146E..0YC. https://wfirst.gsfc.nasa.gov/science/sdt_public/spie/81460Y_1.pdf.
 |
