B-coloring
From HandWiki
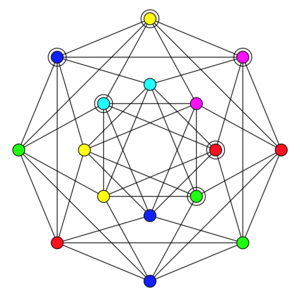
Example of B-coloring of Shrikhande graph with 6 colors: highlighted nodes have neighbors in each other colors. Since each node is adjacent to another 6, a 7-color B-coloring may be possible.
In graph theory, a b-coloring of a graph is a coloring of the vertices where each color class contains a vertex that has a neighbor in all other color classes.
The b-chromatic number of a G graph is the largest b(G) positive integer that the G graph has a b-coloring with b(G) number of colors.
Victor Campos, Carlos Lima és Ana Silva[1] used the relation between b-coloring and a graph's smallest cycle to partly prove the Erdős–Faber–Lovász conjecture.
References
- ↑ V. Campos, C. Lima, A. Silva: "b-coloring graphs with girth at least 8." The Seventh European Conference on Combinatorics, Graph Theory and Applications. Scuola Normale Superiore (2013).
 |

