Bang's theorem on tetrahedra
From HandWiki
Short description: On angles formed when a sphere is inscribed within a tetrahedron
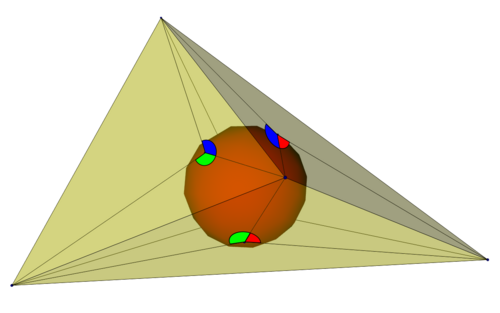
In geometry, Bang's theorem on tetrahedra states that, if a sphere is inscribed within a tetrahedron, and segments are drawn from the points of tangency to each vertex on the same face of the tetrahedron, then all four points of tangency have the same triple of angles. In particular, it follows that the 12 triangles into which the segments subdivide the faces of the tetrahedron form congruent pairs across each edge of the tetrahedron.[1] It is named after A. S. Bang, who posed it as a problem in 1897.[2]
References
- ↑ Brown, B. H. (April 1926), "Theorem of Bang. Isosceles tetrahedra", American Mathematical Monthly 33 (4): 224–226, doi:10.1080/00029890.1926.11986564.
- ↑ "Opgaver til Løsning" (in Danish), Nyt Tidsskrift for Matematik 8 (A): 48, 1897, problem 266.
 |