Bifolium

Short description: Quartic plane curve

Bifolium with a = 1

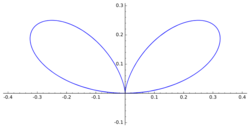
A bifolium is a quartic plane curve with equation in Cartesian coordinates:

[math]\displaystyle{ (x^2 + y^2)^2 = ax^2y. }[/math]

Construction and equations

Construction of the bifolium

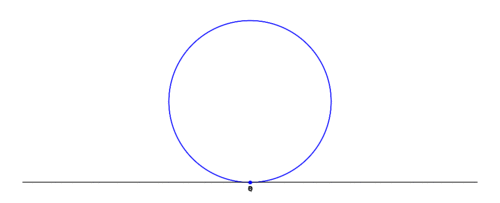
Given a circle C through a point O, and line L tangent to the circle at point O: for each point Q on C, define the point P such that PQ is parallel to the tangent line L, and PQ = OQ. The collection of points P forms the bifolium.

In polar coordinates, the bifolium's equation is

[math]\displaystyle{ \rho = a \sin\theta \cos^2\theta. }[/math]

For a = 1, the total included area is approximately 0.10.

External links

• Bifolium at MathWorld