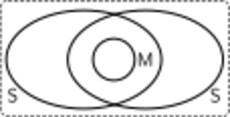
Bigraph
A bigraph can be modelled as the superposition of a graph (the link graph) and a set of trees (the place graph).[1][2]
Each node of the bigraph is part of a graph and also part of some tree that describes how the nodes are nested. Bigraphs can be conveniently and formally displayed as diagrams.[1] They have applications in the modelling of distributed systems for ubiquitous computing and can be used to describe mobile interactions. They have also been used by Robin Milner in an attempt to subsume Calculus of Communicating Systems (CCS) and π-calculus.[2] They have been studied in the context of category theory.[3][4]
Anatomy of a bigraph
Aside from nodes and (hyper-)edges, a bigraph may have associated with it one or more regions which are roots in the place forest, and zero or more holes in the place graph, into which other bigraph regions may be inserted. Similarly, to nodes we may assign controls that define identities and an arity (the number of ports for a given node to which link-graph edges may connect). These controls are drawn from a bigraph signature. In the link graph we define inner and outer names, which define the connection points at which coincident names may be fused to form a single link.
Foundations
A bigraph is a 5-tuple:
[math]\displaystyle{ (V,E,ctrl,prnt,link) : \langle k,X \rangle \to \langle m,Y \rangle, }[/math]
where [math]\displaystyle{ V }[/math] is a set of nodes, [math]\displaystyle{ E }[/math] is a set of edges, [math]\displaystyle{ ctrl }[/math] is the control map that assigns controls to nodes, [math]\displaystyle{ prnt }[/math] is the parent map that defines the nesting of nodes, and [math]\displaystyle{ link }[/math] is the link map that defines the link structure.
The notation [math]\displaystyle{ \langle k,X \rangle \to \langle m,Y \rangle }[/math] indicates that the bigraph has [math]\displaystyle{ k }[/math] holes (sites) and a set of inner names [math]\displaystyle{ X }[/math] and [math]\displaystyle{ m }[/math] regions, with a set of outer names [math]\displaystyle{ Y }[/math]. These are respectively known as the inner and outer interfaces of the bigraph.
Formally speaking, each bigraph is an arrow in a symmetric partial monoidal category (usually abbreviated spm-category) in which the objects are these interfaces.[5] As a result, the composition of bigraphs is definable in terms of the composition of arrows in the category.
Extensions and variants
Directed Bigraphs
Directed Bigraphs[7] are a generalisation of bigraphs where hyper-edges of the link-graph are directed. Ports and names of the interfaces are extended with a polarity (positive or negative) with the requirement that the direction of hyper-edges goes from negative to positive.
Directed bigraphs were introduced as a meta-model for describing computation paradigms dealing with locations and resource communication where a directed link-graph provides a natural description of resource dependencies or information flow. Examples of areas of applications are security protocols,[8] resource access management,[9] and cloud computing.[6]
Bigraphs with sharing
Bigraphs with sharing[10] are a generalisation of Milner's formalisation that allows for a straightforward representation of overlapping or intersecting spatial locations. In bigraphs with sharing, the place graph is defined as a directed acyclic graph (DAG), i.e. [math]\displaystyle{ prnt }[/math] is a binary relation instead of a map. The definition of link graph is unaffected by the introduction of sharing. Note that standard bigraphs are a sub-class of bigraphs with sharing.
Areas of application of bigraphs with sharing include wireless networking protocols,[11] real-time management of domestic wireless networks[12] and mixed reality systems.[13]
Tools and Implementations
- BigraphER is a modelling and reasoning environment for bigraphs consisting of an OCaml library and a command-line tool providing an efficient implementation of rewriting, simulation, and visualisation for both bigraphs and bigraphs with sharing.[14]
- jLibBig is a Java library providing efficient and extensible implementation of bigraphical reactive systems for both bigraphs and directed bigraphs.[15][16]
No longer actively developed:
- BigMC is model checker for bigraphs which includes a command line interface and visualisation.[17]
- Big Red is a graphical editor for bigraphs with easily extensible support for various file formats.[18]
- SBAM is a stochastic simulator for bigraphs, aimed at simulation of biological models.[19]
- DBAM is a distributed simulator for bigraphical reactive systems.[20]
- DBtk is a toolkit for directed bigraphs that provides calculation of IPOs, matching, and visualisation.[21]
See also
Bibliography
- Milner, Robin (2009). The Space and Motion of Communicating Agents. Cambridge University Press. ISBN 978-0521738330.
- Milner, Robin (2001). "Bigraphical reactive systems, (invited paper)". 2154. Springer-Verlag. pp. 16–35. doi:10.1007/3-540-44685-0_2.
- Milner, Robin (2002). "Bigraphs as a Model for Mobile Interaction (invited paper)". 2505. Springer-Verlag. pp. 8–13. doi:10.1007/3-540-45832-8_3.
- Debois, Søren; Damgaard, Troels Christoffer (2005). "Bigraphs by Example". IT University Technical Report Series TR-2005-61. Denmark: IT University of Copenhagen. ISBN 978-87-7949-090-1.
- Sevegnani, Michele; Calder, Muffy (2015). "Bigraphs with sharing". Theoretical Computer Science 577: 43–73. doi:10.1016/j.tcs.2015.02.011.
References
- ↑ 1.0 1.1 A Brief Introduction To Bigraphs, IT University of Copenhagen, Denmark.
- ↑ 2.0 2.1 Milner, Robin. The Bigraphical Model, University of Cambridge Computer Laboratory, UK.
- ↑ Milner, Robin (2008). "Bigraphs and Their Algebra". Electronic Notes in Theoretical Computer Science 209: 5–19. doi:10.1016/j.entcs.2008.04.002. https://www.pure.ed.ac.uk/ws/files/15231681/Bigraphs_and_Their_Algebra.pdf.
- ↑ Miculan, Marino; Peressotti, Marco (2013). Bigraphs reloaded: a presheaf presentation. https://users.dimi.uniud.it/~marino.miculan/Papers/UDMI012013.pdf.
- ↑ Milner, Robin (2009). "Bigraphical Categories". 5710. Springer-Verlag. pp. 30–36. doi:10.1007/978-3-642-04081-8_3.
- ↑ 6.0 6.1 Burco, Fabio; Miculan, Marino; Peressotti, Marco (2020-03-30). "Towards a formal model for composable container systems" (in en). Proceedings of the 35th Annual ACM Symposium on Applied Computing. Brno Czech Republic: ACM. pp. 173–175. doi:10.1145/3341105.3374121. ISBN 978-1-4503-6866-7. https://dl.acm.org/doi/10.1145/3341105.3374121.
- ↑ Grohmann, Davide; Miculan, Marino (2007). "Directed Bigraphs" (in en). Electronic Notes in Theoretical Computer Science 173: 121–137. doi:10.1016/j.entcs.2007.02.031. https://linkinghub.elsevier.com/retrieve/pii/S157106610700103X.
- ↑ Grohmann, Davide (2008), Ehrig, Hartmut; Heckel, Reiko; Rozenberg, Grzegorz et al., eds., "Security, Cryptography and Directed Bigraphs" (in en), Graph Transformations, Lecture Notes in Computer Science (Berlin, Heidelberg: Springer) 5214: pp. 487–489, doi:10.1007/978-3-540-87405-8_41, ISBN 978-3-540-87404-1, http://link.springer.com/10.1007/978-3-540-87405-8_41, retrieved 2021-01-11
- ↑ Grohmann, Davide; Miculan, Marino (2008-07-13). "Controlling resource access in Directed Bigraphs" (in en). Electronic Communications of the EASST: Volume 10: Graph Transformation and Visual Modeling Techniques 2008. doi:10.14279/TUJ.ECEASST.10.142. http://journal.ub.tu-berlin.de/eceasst/article/view/142.
- ↑ Sevegnani, Michele; Calder, Muffy (2015). "Bigraphs with sharing". Theoretical Computer Science 577: 43–73. doi:10.1016/j.tcs.2015.02.011.
- ↑ Calder, Muffy; Sevegnani, Michele (2014). "Modelling IEEE 802.11 CSMA/CA RTS/CTS with stochastic bigraphs with sharing". Formal Aspects of Computing 26 (3): 537–561. doi:10.1007/s00165-012-0270-3.
- ↑ Calder, Muffy; Koliousis, Alexandros; Sevegnani, Michele; Sventek, Joseph (2014). "Real-time verification of wireless home networks using bigraphs with sharing". Science of Computer Programming 80: 288–310. doi:10.1016/j.scico.2013.08.004.
- ↑ Benford, Steve; Calder, Muffy; Rodden, Tom; Sevegnani, Michele (2016-05-01). "On Lions, Impala, and Bigraphs: Modelling Interactions in Physical/Virtual Spaces". ACM Trans. Comput.-Hum. Interact. 23 (2): 9:1–9:56. doi:10.1145/2882784. ISSN 1073-0516. http://eprints.nottingham.ac.uk/39044/1/main_savannah-accepted.pdf.
- ↑ Sevegnani, Michele; Calder, Muffy (2016-07-17). Chaudhuri, Swarat. ed (in en). Computer Aided Verification. Lecture Notes in Computer Science. Springer International Publishing. pp. 494–501. doi:10.1007/978-3-319-41540-6_27. ISBN 9783319415390. http://eprints.gla.ac.uk/119384/13/119384.pdf.
- ↑ Chiapperini, Alessio; Miculan, Marino; Peressotti, Marco (2020). Gadducci, Fabio; Kehrer, Timo. eds. "Computing Embeddings of Directed Bigraphs" (in en). Graph Transformation. Lecture Notes in Computer Science (Cham: Springer International Publishing) 12150: 38–56. doi:10.1007/978-3-030-51372-6_3. ISBN 978-3-030-51372-6.
- ↑ Chiapperini, Alessio; Miculan, Marino; Peressotti, Marco (2022-09-01). "Computing (optimal) embeddings of directed bigraphs" (in en). Science of Computer Programming 221: 102842. doi:10.1016/j.scico.2022.102842. ISSN 0167-6423. https://www.sciencedirect.com/science/article/pii/S0167642322000752.
- ↑ Perrone, Gian; Debois, Søren; Hildebrandt, Thomas T. (2012). "A model checker for Bigraphs" (in en). Proceedings of the 27th Annual ACM Symposium on Applied Computing. Trento, Italy: ACM Press. pp. 1320–1325. doi:10.1145/2245276.2231985. ISBN 978-1-4503-0857-1. http://dl.acm.org/citation.cfm?doid=2245276.2231985.
- ↑ Faithfull, Alexander John; Perrone, Gian; Hildebrandt, Thomas T. (2013-06-25). "Big Red: A Development Environment for Bigraphs" (in en). Electronic Communications of the EASST: Volume 61: Graph Computation Models 2012. doi:10.14279/TUJ.ECEASST.61.835. http://journal.ub.tu-berlin.de/eceasst/article/view/835.
- ↑ Krivine, Jean; Milner, Robin; Troina, Angelo (2008-10-22). "Stochastic Bigraphs" (in en). Electronic Notes in Theoretical Computer Science. Proceedings of the 24th Conference on the Mathematical Foundations of Programming Semantics (MFPS XXIV) 218: 73–96. doi:10.1016/j.entcs.2008.10.006. ISSN 1571-0661. http://www.sciencedirect.com/science/article/pii/S1571066108004003.
- ↑ Mansutti, Alessio; Miculan, Marino; Peressotti, Marco (2015-09-06). "Distributed execution of bigraphical reactive systems" (in en). Electronic Communications of the EASST: Volume 71: Graph Computation Models 2014. doi:10.14279/TUJ.ECEASST.71.994. http://journal.ub.tu-berlin.de/eceasst/article/view/994.
- ↑ Bacci, Giorgio; Grohmann, Davide; Miculan, Marino (2009), Kurz, Alexander; Lenisa, Marina; Tarlecki, Andrzej, eds., "DBtk: A Toolkit for Directed Bigraphs", Algebra and Coalgebra in Computer Science (Berlin, Heidelberg: Springer Berlin Heidelberg) 5728: pp. 413–422, doi:10.1007/978-3-642-03741-2_28, ISBN 978-3-642-03740-5, Bibcode: 2009LNCS.5728..413B, http://link.springer.com/10.1007/978-3-642-03741-2_28, retrieved 2021-01-18
External links
 |