Biography:Charles Jean de la Vallée Poussin
Baron Charles Jean de la Vallée Poussin | |
|---|---|
 Poussin, c. 1900 | |
| Born | Charles-Jean Étienne Gustave Nicolas, baron de la Vallée Poussin 14 August 1866 Leuven, Belgium |
| Died | 2 March 1962 (aged 95) Watermael-Boitsfort, Brussels, Belgium |
| Citizenship | Belgium |
| Alma mater | Catholic University of Leuven (1834–1968) |
| Known for | Poussin graph Poussin summability Poussin theorem Prime number theorem |
| Awards | Poncelet Prize (1916) |
| Scientific career | |
| Fields | Mathematics |
| Institutions | Catholic University of Leuven (1834–1968) |
| Doctoral students | Georges Lemaître |
Charles-Jean Étienne Gustave Nicolas, baron de la Vallée Poussin (French pronunciation: [ʃaʁl ʒɑ̃ etjɛn ɡystav nikɔla baʁɔ̃ də la vale pusɛ̃]; 14 August 1866 – 2 March 1962) was a Belgian mathematician. He is best known for proving the prime number theorem.
The King of Belgium ennobled him with the title of baron.
Biography
De la Vallée Poussin was born in Leuven, Belgium. He studied mathematics at the Catholic University of Leuven under his uncle Louis-Philippe Gilbert, after he had earned his bachelor's degree in engineering. De la Vallée Poussin was encouraged to study for a doctorate in physics and mathematics, and in 1891, at the age of just 25, he became an assistant professor in mathematical analysis.
De la Vallée Poussin became a professor at the same university (as was his father, Charles Louis de la Vallée Poussin, who taught mineralogy and geology) in 1892. De la Vallée Poussin was awarded with Gilbert's chair when Gilbert died. While he was a professor there, de la Vallée Poussin carried out research in mathematical analysis and the theory of numbers, and in 1905 was awarded the Decennial Prize for Pure Mathematics 1894–1903. He was awarded this prize a second time in 1924 for his work during 1914–23.
In 1898, de la Vallée Poussin was appointed as the correspondent to the Royal Belgian Academy of Sciences, and he became a Member of the Academy in 1908. In 1923, he became the President of the Division of Sciences.
In August 1914, de la Vallée Poussin escaped from Leuven at the time of its destruction by the invading German Army of World War I, and he was invited to teach at Harvard University in the United States . He accepted this invitation. In 1918, de la Vallée Poussin returned to Europe to accept professorships in Paris at the Collège de France and at the Sorbonne.
After the war was over, de la Vallée Poussin returned to Belgium, The International Union of Mathematicians was created, and he was invited to become its President. Between 1918 and 1925, de la Vallée Poussin traveled extensively, lecturing in Geneva, Strasbourg, and Madrid. and then in the United States where he gave lectures at the Universities of Chicago, California, Pennsylvania, and Brown University, Yale University, Princeton University, Columbia University, and the Rice Institute of Houston.
He was awarded the Prix Poncelet for 1916.[1] De la Vallée Poussin was given the titles of Doctor Honoris Causa of the Universities of Paris, Toronto, Strasbourg, and Oslo, an Associate of the Institute of France, and a Member of the Pontifical Academy of Sciences,[2] Nazionale dei Lincei, Madrid, Naples, Boston. He was awarded the title of Baron by King Albert I of the Belgians in 1928.
In 1961, de la Vallée Poussin fractured his shoulder, and this accident and its complications led to his death in Watermael-Boitsfort, near Brussels, Belgium, a few months later.[3]
A student of his, Georges Lemaître, was the first to propose the Big Bang theory of the formation of the Universe.
Work
Although his first mathematical interests were in analysis, he became suddenly famous as he proved the prime number theorem independently of his coeval Jacques Hadamard in 1896.
Afterwards, he found interest in approximation theory. He defined, for any continuous function f on the standard interval [math]\displaystyle{ [-1, 1] }[/math], the sums
- [math]\displaystyle{ V_n=\frac{S_n+S_{n+1}+\cdots+S_{2n-1}}{n} }[/math],
where
- [math]\displaystyle{ S_n=\frac{1}{2}c_0(f)+\sum_{i=1}^n c_i(f) T_i }[/math]
and
- [math]\displaystyle{ c_i(f) \, }[/math]
are the vectors of the dual basis with respect to the basis of Chebyshev polynomials (defined as
- [math]\displaystyle{ (T_0/2,T_1,\ldots,T_n). }[/math]
Note that the formula is also valid with [math]\displaystyle{ S_n }[/math] being the Fourier sum of a [math]\displaystyle{ 2\pi }[/math]-periodic function [math]\displaystyle{ F }[/math] such that
- [math]\displaystyle{ F(\theta)=f(\cos\theta). \, }[/math]
Finally, the de la Vallée Poussin sums can be evaluated in terms of the so-called Fejér sums (say [math]\displaystyle{ F_n }[/math])
- [math]\displaystyle{ V_n=2F_{2n-1}-F_{n-1}. \, }[/math]
The kernel is bounded ([math]\displaystyle{ V_n \le 3 }[/math]) and obeys the property
- [math]\displaystyle{ f*V_n = f \, }[/math], if [math]\displaystyle{ f(x)= \sum_{j=-n}^n a_j e^{i j x}. \, }[/math]
Later, he worked on potential theory and complex analysis.
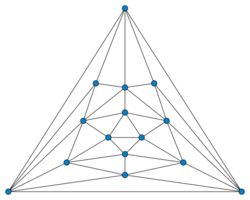
He also published a counterexample to Alfred Kempe's false proof of the four color theorem. The Poussin graph, the graph he used for this counterexample, is named after him.
Cours d’analyse
The textbooks of his mathematical analysis course have been a reference for a long time and had some international influence.[4]
The second edition (1909-1912) is remarkable for its introduction of the Lebesgue integral. It was in 1912, "the only textbook on analysis containing both Lebesgue integral and its application to Fourier series, and a general theory of approximation of functions by polynomials".[4]
The third edition (1914) introduced the now classical definition of differentiability due to Otto Stolz. The second volume of this third edition was burnt in the fire of Louvain during the German invasion.
The further editions were much more conservative, returning essentially to the first edition. Starting from the eight edition, Fernand Simonart took over the revision and the publication of the Cours d’analyse.
Selected publications
- Œuvres, vol. 1 (Biography and number theory), 2000 (eds. Mawhin, Butzer, Vetro), vols. 2 to 4 planned
- Cours d´Analyse, 2 vols., 1903, 1906 (7th edition 1938), Reprint of the 2nd edition 1912, 1914 by Jacques Gabay, ISBN 2-87647-227-9 (deals only with real analysis).[5] Online:
- Integrals de Lebesgue, fonctions d´ensemble, classes de Baire,[7] 2nd edition 1934, Reprint by Jacques Gabay, ISBN 2-87647-159-0
- Le potentiel logarithmique, balayage et representation conforme, Paris, Löwen 1949
- Recherches analytiques de la théorie des nombres premiers, Annales de la Societe Scientifique de Bruxelles vol. 20 B, 1896, pp. 183–256, 281–362, 363–397, vol. 21 B, pp. 351–368 (prime number theorem)
- Sur la fonction Zeta de Riemann et le nombre des nombres premiers inferieur a une limite donnée, Mémoires couronnés de l Academie de Belgique, vol.59, 1899, pp. 1–74
- Leçons sur l'approximation des fonctions d'une variable réelle Paris, Gauthier-Villars, 1919,[8] 1952
See also
- Poussin proof
- Remez algorithm
- La Vallée-Poussin
Notes
- ↑ "Prix Poncelet". Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences: 791. 18 December 1916. http://visualiseur.bnf.fr/CadresFenetre?O=NUMM-3116&I=791&M=notice.
- ↑ "Charles de la Vallee Poussin". http://www.casinapioiv.va/content/accademia/en/academicians/deceased/delavalleepoussin.html.
- ↑ Burkill, J. C. (1964). "Charles-Joseph de la Vallée Poussin". Journal of the London Mathematical Society: 165–175. doi:10.1112/jlms/s1-39.1.165. https://doi.org/10.1112/jlms/s1-39.1.165.
- ↑ 4.0 4.1 Mawhin, Jean (19 September 2014). "The Cours d'Analyse Infinitésimale of Charles-Jean de La Vallée Poussin: From Innovation to Tradition" (in en). Jahresbericht der Deutschen Mathematiker-Vereinigung 116 (4): 243–259. doi:10.1365/s13291-014-0100-z. ISSN 0012-0456.
- ↑ Porter, M. B. (1915). "Review: Cours d'Analyse Infinitésmale, by Ch.-J. de la Vallée Poussin". Bull. Amer. Math. Soc. 22 (2): 77–85. doi:10.1090/s0002-9904-1915-02725-4. https://www.ams.org/journals/bull/1915-22-02/S0002-9904-1915-02725-4/S0002-9904-1915-02725-4.pdf.
- ↑ Porter, M. B. (1925). "Review: Cours d'Analyse Infinitésimale, Tome I, by Ch. J. de la Vallée Poussin". Bull. Amer. Math. Soc. 31 (1): 83. doi:10.1090/s0002-9904-1925-04009-4. https://www.ams.org/journals/bull/1925-31-01/S0002-9904-1925-04009-4/S0002-9904-1925-04009-4.pdf.
- ↑ Carmichael, R. D. (1918). "Review: Integrals de Lebesgue, Fonctions d'Ensemble, Classes de Baire, by C. de la Vallée Poussin". Bull. Amer. Math. Soc. 24 (7): 348–355. doi:10.1090/s0002-9904-1918-03091-7. https://www.ams.org/journals/bull/1918-24-07/S0002-9904-1918-03091-7/S0002-9904-1918-03091-7.pdf.
- ↑ Jackson, Dunham (1922). "Review: Leçons sur l'approximation des fonctions d'une variable réelle, by C. de la Vallée Poussin". Bull. Amer. Math. Soc. 28 (1): 59–61. doi:10.1090/S0002-9904-1922-03513-6. https://www.ams.org/journals/bull/1922-28-01/S0002-9904-1922-03513-6/S0002-9904-1922-03513-6.pdf.
External links
- Charles Jean de la Vallée Poussin at the Mathematics Genealogy Project
- Biographie Universelle, by Didot.
- O'Connor, John J.; Robertson, Edmund F., "Charles Jean de la Vallée Poussin", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Vallee_Poussin.html.
 |

