Poussin graph

From HandWiki
Poussin graph
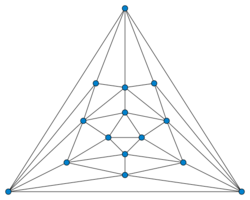Poussin graph planar.svg
Vertices15
Edges39
Radius3
Diameter3
Girth3
Automorphisms2 (Z/2Z)
Chromatic number4
Chromatic index6
PropertiesHamiltonian
Planar
Table of graphs and parameters
Tangled Kempe chains in the Poussin graph. The adjacencies between regions of this map form the Poussin graph, partially four-colored with the outer region uncolored. The blue–yellow and blue–green Kempe chains (yellow and green lines) connect the outer region's neighbors, so Kempe would swap colors in the left red–yellow chain and the right red–green chain (red lines), allowing the outer region to be red. As the blue–yellow and blue–green chains cross, this color swap would cause the upper yellow and green regions to both become red, producing an invalid coloring.

In graph theory, the Poussin graph is a planar graph with 15 vertices and 39 edges. It is named after Charles Jean de la Vallée-Poussin.

History

In 1879, Alfred Kempe published a proof of the four color theorem, one of the big conjectures in graph theory.[1] While the theorem is true, Kempe's proof is incorrect. Percy John Heawood illustrated it in 1890[2] with a counter-example, and de la Vallée-Poussin reached the same conclusion in 1896 with the Poussin graph.[3]

Kempe's (incorrect) proof is based on alternating chains, and as those chains prove useful in graph theory mathematicians remain interested in such counterexamples. More were found later: first, the Errera graph in 1921,[4][5] then the Kittell graph in 1935, with 23 vertices,[6] and finally two minimal counter-examples (the Soifer graph in 1997 and the Fritsch graph in 1998, both of order 9).[7][8][9]

References

  1. ↑ Kempe, A. B. "On the Geographical Problem of Four-Colors." Amer. J. Math. 2, 193–200, 1879.
  2. ↑ P. J. Heawood, "Map colour theorem", Quart. J. Pure Appl. Math. 24 (1890), 332–338.
  3. ↑ R. A. Wilson, Graphs, colourings and the four-colour theorem, Oxford University Press, Oxford, 2002. MR1888337 Zbl 1007.05002.
  4. ↑ Errera, A. "Du coloriage des cartes et de quelques questions d'analysis situs." Ph.D. thesis. 1921.
  5. ↑ Peter Heinig. Proof that the Errera Graph is a narrow Kempe-Impasse. 2007.
  6. ↑ Kittell, I. "A Group of Operations on a Partially Colored Map." Bull. Amer. Math. Soc. 41, 407–413, 1935.
  7. ↑ A. Soifer, “Map coloring in the victorian age: problems and history”, Mathematics Competitions 10 (1997), 20–31.
  8. ↑ R. Fritsch and G. Fritsch, The Four-Color Theorem, Springer, New York, 1998. MR1633950.
  9. ↑ Gethner, E. and Springer, W. M. II. « How False Is Kempe's Proof of the Four-Color Theorem? » Congr. Numer. 164, 159–175, 2003.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Poussin_graph&oldid=107346"