Biology:Effect of gait parameters on energetic cost

From HandWiki
Short description: Gait relationship

The effect of gait parameters on energetic cost is a relationship that describes how changes in step length, cadence, step width, and step variability influence the mechanical work and metabolic cost involved in gait. The source of this relationship stems from the deviation of these gait parameters from metabolically optimal values, with the deviations due to environmental, pathological, and other factors.

Tracking of metabolic activity via VO2 measurement during treadmill walking.

Cost of transport [COT]

In human gait, to travel a particular distance, chemical energy must be expended by the body. This relationship can be expressed by the dimensionless term, cost of transport (COT).,[1] that describes the amount of metabolic energy needed to move a body a unit of distance. Healthy humans walking at self-selected speeds have a cost of transport of approximately 0.8 calorie/meter/kilogram.[2] Depending on speed, stability conditions, and other internal and external factors,[3][4][5] the cost of transport for gait can change. These measured metabolic changes are attributed to variations in step length, step width, and other parameters of gait, which have a direct bearing on COT[6][7]

Preferred Gait

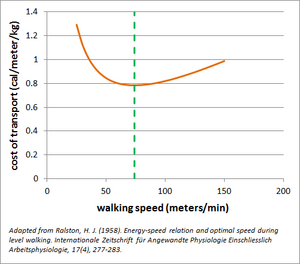
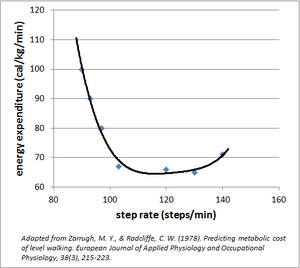
Qualitative illustration of the relationship between walking speed and cost of transport (COT). The green line indicates the walking speed with minimum COT.
Qualitative illustration of the relationship between step rate (or cadence) and rate of energy expenditure at a fixed walking speed of ~90 m/min.

Metabolic cost is naturally optimized by selection of a nominal gait. While external factors such as instability and perceived dangers may temporarily alter the body's priorities,[3] the primary goal of minimizing a task-dependent energetic expenditure[8] ultimately dominates the determination of preferred walking gait. As a result, humans tend to select a preferred walking speed that minimizes their cost of transport. The relationship between walking and cost of transport is parabola-like with the preferred walking speed at the minimum, meaning walking at a slower or faster speed can incur a similar increase in energetic cost for a 1-kilometer walk.[1] Within each walking speed, the step length and cadence are also optimized for metabolic cost. While multiple proportional combinations of step length and cadence can be used to achieve the same walking speed, taking faster and shorter steps or slower and longer steps than the optimal combination leads to increased cost of transport.[9]

Gait Parameter Definitions

The parameters of gait for a fixed walking speed all vary with the size (e.g. leg length) of different individuals. However, a typical or average self-selected value can be estimated based on average human size. The mechanical work and metabolic cost associated with these parameters can be described by the dynamic walking model.

Step Length

Step length is a measure of the distance, parallel to the direction of travel, between the initial point of contact of one foot and the successive initial point of contact of the opposite foot. The step lengths for left and right are similar in normal gait. Another metric similar to step length is known as stride length, which measures the distance between successive points of initial contact of the same foot, and left and right stride lengths are normally equivalent. At self-selected walking speeds, normal step length is approximately 0.75 meters for men and slightly less for women due to a gender-specific shorter average leg length.[1][9][10] For other walking speeds, the preferred step length can be approximately predicted based on the relationship [math]\displaystyle{ \textstyle s \; \alpha \; v^{0.42} }[/math], where [math]\displaystyle{ \textstyle s }[/math] is step length and [math]\displaystyle{ \textstyle v }[/math] is walking speed.[11]

Cadence

Cadence is a metric of walking rate, typically measured in number of steps per minute. This parameter is also termed as step frequency. At self-selected walking speeds, the step frequency is approximately 100 steps/min.[2][12]

Step Width

Step width is a measure of the distance, perpendicular to the each foot midline, between the initial point of contact of one foot and the successive initial point of contact of the opposite foot. At self-selected walking speeds, step width is typically around 10 to 12 cm. This is based on the relationship that equates step width to [math]\displaystyle{ \textstyle 0.12L }[/math], where [math]\displaystyle{ \textstyle L }[/math] is leg length.[13]

Step Variability

Step variability is a measure of the standard deviation of step length and step width calculated from all valid steps during a single walking trial. At self-selected walking speeds, step width variability (~2.8 cm) is almost always greater than step length variability (~1.8 cm)[7][14]

Dynamic Walking as a Framework for COT

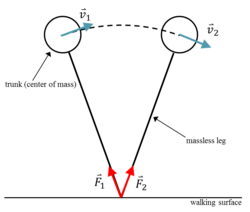
Center of mass on a massless leg travelling along the trunk trajectory path in inverted pendulum theory. Velocity vectors are shown perpendicular to the ground reaction force at time 1 and time 2.

In dynamic walking, the human body can be modeled as the center of mass (COM) supported by a massless rigid leg in single support and two massless legs during double-support,[15] which is consistent with passive dynamics of the inverted pendulum, otherwise known as the inverted pendulum theory of gait. In single support, no work is done since the ground reaction force is perpendicular to the COM motion. In double support, the trailing leg works in conjunction with the leading leg to redirect the COM motion upward. During this step-to-step transition period, the trailing leg exerts positive mechanical work on the COM while the leading leg exerts negative mechanical work on the COM. To maintain steady walking gait requires the sum of these work terms, or the net work, to be equal to zero since any changes in system energy would impart different COM velocities between the start and end of transition. While the ideal net mechanical work of this system is zero, muscle contractions are necessary to generate the ground reaction forces, implying that the metabolic energy expended is nonzero.

Leg Swing Mechanics

The massless leg assumption in the inverted pendulum theory omits the amount of work required to swing the contralateral leg during single support. Due to the similarity of leg swing with the hanging pendulum paradigm, the work performed is dominated by gravity.[16] In the case that the leg is swung at a rate outside of the natural frequency, the hip torque generated by muscle action becomes significantly larger. For typical steady gait, it is approximated that the energy expended to perform leg swing accounts for 10% to 30% of the total metabolic energy consumed.[17][18]

Gait Parameters and Energetic Cost

Changes to each individual gait parameter affects the energetic cost of walking. However, these same changes also affect other gait parameters, leading to trade offs that require the human body to apply optimizations that minimize energetic cost.

  • Step Length

Energetic cost increases with longer step lengths due to increased ground reaction forces during double-support and more hip torque during the swing phase. According to the dynamic walking model, mechanical work in the step-to-step transitions increases proportional to step length and can be described by [math]\displaystyle{ \textstyle \dot{W} \; \alpha \; l^4 }[/math], where [math]\displaystyle{ \textstyle \dot{W} }[/math] is mechanical work rate and [math]\displaystyle{ \textstyle l }[/math] is step length, which equates to a proportional increase in net metabolic rate.[19] This relationship is due to reduced vertical force contribution for redirecting the COM at the wider step angles associated with longer step lengths. Larger step lengths also require additional hip torque during the swing phase to travel a wider angle, which contributes to the rate of metabolic cost by a factor of leg length squared[15]

  • Cadence

Increase in cadence yields more instances of leg swings and step-to-step transitions within a unit of time, leading to an increase in the rate of energetic cost. The relationship between mechanical work and step frequency can be described by [math]\displaystyle{ \textstyle \dot{W} \; \alpha \; f^3 }[/math] for the step-to-step transitions, where [math]\displaystyle{ \textstyle \dot{W} }[/math] is the mechanical work rate and [math]\displaystyle{ \textstyle f }[/math] is the step frequency.[19] Rate of metabolic cost also follows this relationship. The impact of cadence on leg swing metabolic cost is approximated as [math]\displaystyle{ \textstyle \dot{E} \; \alpha \; f^4 }[/math], where [math]\displaystyle{ \textstyle \dot{E} }[/math] is the rate of metabolic cost and [math]\displaystyle{ \textstyle f }[/math] is the step frequency[17]

  • Step Width

Similar to selection of stride length and frequency, humans also select for a metabolically optimal step width.[6] Adopting a wider stance increases the stability of a passive dynamic system, as well as increases the lateral clearance of the swing leg from the stance leg.[20] According to the dynamic walking model, the mediolateral "rocking" of the legs can be also described by the inverted pendulum paradigm, and a wider stance would similarly require increased ground reaction force to redirect the COM, and thus increase the metabolic demand. For a narrower stance, due to insufficient clearance, hip torque may be increased to project the swing leg out laterally, leading to increased metabolic cost as well.[6] The relationship between step width and energetic cost for the step-to-step transitions can be described as [math]\displaystyle{ \textstyle \dot{E} \; \alpha \; \dot{W} \; \alpha \; w^2 }[/math], where [math]\displaystyle{ \textstyle \dot{E} }[/math] is the rate of metabolic cost, [math]\displaystyle{ \textstyle \dot{W} }[/math] is the mechanical work rate, and [math]\displaystyle{ \textstyle w }[/math] is the step width.

  • Step Variability

Step width variability is associated with the active control of the nervous system for walking stability, and is reduced in the presence of external stabilizers[4][21] while increased with exposure to balance perturbations.[7] Step length variability is similarly attributed due to a coupling that exists between medio-lateral and fore-aft motion in walking, but to a diminished degree.[13] Step width variability is positively correlated with rate of metabolic cost, and with respect to the variability associated with mediolateral balance, accounts for about 6% of metabolic cost in preferred gait.[13] While some of the energetic cost encountered with step variability may arise due to the net changes in step width and step length, there exists a portion of the cost that can be attributed to the effort of stability control during walking.

Constrained Optimization

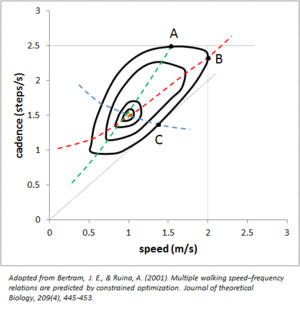
Energetic Cost Contour Plot. Coutour lines represent parameter combinations that require the same cost of transport. The colored lines represent optimization to different parameters: (green) step frequency; (red) walking speed; (blue)step length.

Since multiple distinct gait parameters have a significant impact on the energetic cost of walking, each of these parameters have to be considered when examining the primary goal of metabolic cost optimization. The visualization of such an optimization for walking speed, cadence, and step length can be expressed in the form of a contour map, in which parameter combinations that lie on the same contour line share the same cost of transport (cal/kg/m).[2][22] The green, red, and blue, dotted lines represent values where cadence, walking speed, and step length are constrained, respectively. These lines can be formed by finding the tangent points that lines representative of several constant parameter values form with the constant COT contours. For example, the optimal COT's for constrained walking speeds (red) can be found by drawing vertical lines and noting where they form a tangent with a contour, as seen with point B in the diagram. A series of these intersections can then form the curve for optimal COT under constrained walking speed. These constrained optimization values not only reflect the naturally selected preferred gait parameters that are observed by fixing a single parameter at different values, but also form part of a predictive map that allows for the identification of the cost of transport for a multivariate system.

See also

  • Preferred walking speed
  • Gait Analysis
  • Passive Dynamics
  • Naismith's rule
  • Walking
  • Running energetics

References

  1. ↑ 1.0 1.1 1.2 Ralston, H. J. (1958). Energy-speed relation and optimal speed during level walking. Internationale Zeitschrift für Angewandte Physiologie Einschliesslich Arbeitsphysiologie, 17(4), 277-283.
  2. ↑ 2.0 2.1 2.2 Zarrugh, M. Y., Todd, F. N., & Ralston, H. J. (1974). Optimization of energy expenditure during level walking. European Journal of Applied Physiology and Occupational Physiology, 33(4), 293-306.
  3. ↑ 3.0 3.1 Voloshina, A. S., Kuo, A. D., Daley, M. A., & Ferris, D. P. (2013). Biomechanics and energetics of walking on uneven terrain. The Journal of Experimental Biology, 216(21), 3963-3970.
  4. ↑ 4.0 4.1 Ijmker, T., Houdijk, H., Lamoth, C. J., Beek, P. J., & van der Woude, L. H. (2013). Energy cost of balance control during walking decreases with external stabilizer stiffness independent of walking speed. Journal of biomechanics,46(13), 2109-2114.
  5. ↑ Detrembleur, C., Dierick, F., Stoquart, G., Chantraine, F., & Lejeune, T. (2003). Energy cost, mechanical work, and efficiency of hemiparetic walking. Gait & posture, 18(2), 47-55.
  6. ↑ 6.0 6.1 6.2 Donelan, J. M., & Kram, R. (2001). Mechanical and metabolic determinants of the preferred step width in human walking. Proceedings of the Royal Society of London. Series B: Biological Sciences, 268(1480), 1985-1992.
  7. ↑ 7.0 7.1 7.2 .O’Connor, S. M., Xu, H. Z., & Kuo, A. D. (2012). Energetic cost of walking with increased step variability. Gait & posture, 36(1), 102-107.
  8. ↑ McNeill Alexander, R. (2002). Energetics and optimization of human walking and running: the 2000 Raymond Pearl memorial lecture. American Journal of Human Biology, 14(5), 641-648.
  9. ↑ 9.0 9.1 Zarrugh, M. Y., & Radcliffe, C. W. (1978). Predicting metabolic cost of level walking. European Journal of Applied Physiology and Occupational Physiology, 38(3), 215-223.
  10. ↑ Sekiya, N., Nagasaki, H., Ito, H., & Furuna, T. (1997). Optimal walking in terms of variability in step length. Journal of Orthopaedic & Sports Physical Therapy, 26(5), 266-272.
  11. ↑ Grieve, D. W. (1968). Gait patterns and the speed of walking. Biomedical Engineering, 3(3), 119-122.
  12. ↑ Cavagna, G. A., & Franzetti, P. (1986). The determinants of the step frequency in walking in humans. The Journal of physiology, 373(1), 235-242.
  13. ↑ 13.0 13.1 13.2 Bauby, C. E., & Kuo, A. D. (2000). Active control of lateral balance in human walking. Journal of biomechanics, 33(11), 1433-1440.
  14. ↑ Owings, T. M., & Grabiner, M. D. (2004). Step width variability, but not step length variability or step time variability, discriminates gait of healthy young and older adults during treadmill locomotion. Journal of biomechanics, 37(6), 935-938.
  15. ↑ 15.0 15.1 Donelan, J. M., Kram, R., & Kuo, A. D. (2002). Mechanical work for step-to-step transitions is a major determinant of the metabolic cost of human walking. Journal of Experimental Biology, 205(23), 3717-3727.
  16. ↑ Mochon, S., & McMahon, T. A. (1980). Ballistic walking: An improved model.Mathematical Biosciences, 52(3), 241-260.
  17. ↑ 17.0 17.1 Doke, J., Donelan, J. M., & Kuo, A. D. (2005). Mechanics and energetics of swinging the human leg. The Journal of Experimental Biology, 208(3), 439-445.
  18. ↑ Gottschall, J. S., & Kram, R. (2005). Energy cost and muscular activity required for leg swing during walking. Journal of Applied Physiology, 99(1), 23-30.
  19. ↑ 19.0 19.1 Kuo, A. D., Donelan, J. M., & Ruina, A. (2005). Energetic consequences of walking like an inverted pendulum: step-to-step transitions. Exercise and sport sciences reviews, 33(2), 88-97.
  20. ↑ Kuo, A. D. (1999). Stabilization of lateral motion in passive dynamic walking. The International journal of robotics research, 18(9), 917-930.
  21. ↑ Donelan, J. M., Shipman, D. W., Kram, R., & Kuo, A. D. (2004). Mechanical and metabolic requirements for active lateral stabilization in human walking. Journal of biomechanics, 37(6), 827-835.
  22. ↑ Bertram, J. E., & Ruina, A. (2001). Multiple walking speed–frequency relations are predicted by constrained optimization. Journal of theoretical Biology, 209(4), 445-453.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Biology:Effect_of_gait_parameters_on_energetic_cost&oldid=3606232"