Biology:Metabolic control analysis

From HandWiki
Short description: Metabolic control
Plot of steady state flux versus enzyme activity with flux control coefficients at various points.

Metabolic control analysis (MCA) is a mathematical framework for describing metabolic, signaling, and genetic pathways. MCA quantifies how variables, such as fluxes and species concentrations, depend on network parameters. In particular, it is able to describe how network-dependent properties, called control coefficients, depend on local properties called elasticities or Elasticity Coefficients.[1][2][3]

MCA was originally developed to describe the control in metabolic pathways but was subsequently extended to describe signaling and genetic networks. MCA has sometimes also been referred to as Metabolic Control Theory, but this terminology was rather strongly opposed by Henrik Kacser, one of the founders[citation needed].

More recent work[4] has shown that MCA can be mapped directly on to classical control theory and are as such equivalent.

Biochemical systems theory[5] (BST) is a similar formalism, though with rather different objectives. Both are evolutions of an earlier theoretical analysis by Joseph Higgins.[6]

Chemical reaction network theory is another theoretical framework that has overlap with both MCA and BST but is considerably more mathematically formal in its approach.[7] It's emphasis is primarily on dynamic stability criteria[8] and related theorems associated with mass-action networks. In more recent years the field has also developed [9] a sensitivity analysis which is similar if not identical to MCA and BST.

Control coefficients

A control coefficient[10] [11][12] measures the relative steady state change in a system variable, e.g. pathway flux (J) or metabolite concentration (S), in response to a relative change in a parameter, e.g. enzyme activity or the steady-state rate ([math]\displaystyle{ v_i }[/math]) of step [math]\displaystyle{ i }[/math]. The two main control coefficients are the flux and concentration control coefficients. Flux control coefficients are defined by

[math]\displaystyle{ C^J_{v_i} = \left( \frac{dJ}{dp} \frac{p}{J} \right) \bigg/ \left( \frac{\partial v_i}{\partial p}\frac{p}{v_i} \right) = \frac{d\ln J}{d\ln v_i} }[/math]

and concentration control coefficients by

[math]\displaystyle{ C^S_{v_i} = \left( \frac{dS}{dp} \frac{p}{S} \right) \bigg/ \left( \frac{\partial v_i}{\partial p} \frac{p}{v_i} \right) = \frac{d\ln S}{d\ln v_i} }[/math]
Control coefficients measure the effect of perturbations in an enzyme on a steady-state observable such as a flux or metabolite concentration. Note that the effect of a perturbation can be positive or negative depending on context. In the figure, a perturbation is assumed to be at step three. Figure modified and redrawn from[13]

.

Summation theorems

The flux control summation theorem was discovered independently by the Kacser/Burns group[10] and the Heinrich/Rapoport group[11] in the early 1970s and late 1960s. The flux control summation theorem implies that metabolic fluxes are systemic properties and that their control is shared by all reactions in the system. When a single reaction changes its control of the flux this is compensated by changes in the control of the same flux by all other reactions.

[math]\displaystyle{ \sum_i C^J_{v_i} = 1 }[/math]
[math]\displaystyle{ \sum_i C^s_{v_i} = 0 }[/math]

Elasticity coefficients

The elasticity coefficient measures the local response of an enzyme or other chemical reaction to changes in its environment. Such changes include factors such as substrates, products, or effector concentrations. For further information, please refer to the dedicated page at elasticity coefficients.

Elasticities are local quantities that measure the effect of substrates, products, and effectors on a given reaction. The vertical black arrows represent enzyme catalysis. Figure redrawn and modified from[14]

.

Connectivity theorems

The connectivity theorems[10][11] are specific relationships between elasticities and control coefficients. They are useful because they highlight the close relationship between the kinetic properties of individual reactions and the system properties of a pathway. Two basic sets of theorems exists, one for flux and another for concentrations. The concentration connectivity theorems are divided again depending on whether the system species [math]\displaystyle{ S_n }[/math] is different from the local species [math]\displaystyle{ S_m }[/math].

[math]\displaystyle{ \sum_i C^J_i \varepsilon^i_s = 0 }[/math]
[math]\displaystyle{ \sum_i C^{s_n}_i \varepsilon^i_{s_m} = 0 \quad n \neq m }[/math]
[math]\displaystyle{ \sum_i C^{s_n}_i \varepsilon^i_{s_m} = -1 \quad n = m }[/math]

Response Coefficient

Kacser and Burns[10] introduced an additional coefficient that described how a biochemical pathway would respond the external environment. They termed this coefficient the response coefficient and designated it using the symbol R. The response coefficient is an important metric because it can be used to assess how much a nutrient or perhaps more important, how a drug can influence a pathway. This coefficient is therefore highly relevant to the pharmaceutical industry.[15]

The response coefficient is related to the core of metabolic control analysis via the response coefficient theorem, which is stated as follows:

[math]\displaystyle{ R^X_m = C^X_{i} \varepsilon^{i}_m }[/math]

where [math]\displaystyle{ X }[/math] is a chosen observable such as a flux or metabolite concentration, [math]\displaystyle{ i }[/math] is the step that the external factor targets, [math]\displaystyle{ C^X_{i} }[/math] is the control coefficient of the target steps, and [math]\displaystyle{ \varepsilon^{i}_m }[/math] is the elasticity of the target step with respect to the external factor [math]\displaystyle{ m }[/math].

The key observation of this theorem is that an external factor such as a therapeutic drug, acts on the organism's phenotype via two influences: 1) How well the drug can affect the target itself through effective binding of the drug to the target protein and its effect on the protein activity. This effectiveness is described by the elasticity [math]\displaystyle{ \varepsilon^{i}_m }[/math] and 2) How well do modifications of the target influence the phenotype by transmission of the perturbation to the rest of the network. This is indicated by the control coefficient [math]\displaystyle{ C^X_{i} }[/math].

A drug action, or any external factor, is most effective when both these factors are strong. For example, a drug might be very effective at changing the activity of its target protein, however if that perturbation in protein activity is unable to be transmitted to the final phenotype then the effectiveness of the drug is greatly diminished.

If a drug or external factor, [math]\displaystyle{ m }[/math], targets multiple sites of action, for example [math]\displaystyle{ n }[/math] sites, then the overall response in a phenotypic factor [math]\displaystyle{ X }[/math], is the sum of the individual responses:

[math]\displaystyle{ R_m^X=\sum_{i=1}^n C_{i}^X \varepsilon_m^{i} }[/math]

Control equations

It is possible to combine the summation with the connectivity theorems to obtain closed expressions that relate the control coefficients to the elasticity coefficients. For example, consider the simplest non-trivial pathway:

[math]\displaystyle{ X_o \rightarrow S \rightarrow X_1 }[/math]

We assume that [math]\displaystyle{ X_o }[/math] and [math]\displaystyle{ X_1 }[/math] are fixed boundary species so that the pathway can reach a steady state. Let the first step have a rate [math]\displaystyle{ v_1 }[/math] and the second step [math]\displaystyle{ v_2 }[/math]. Focusing on the flux control coefficients, we can write one summation and one connectivity theorem for this simple pathway:

[math]\displaystyle{ C^J_{v_1} + C^J_{v_2} = 1 }[/math]
[math]\displaystyle{ C^J_{v_1} \varepsilon^{v_1}_s + C^J_{v_2} \varepsilon^{v_2}_s = 0 }[/math]

Using these two equations we can solve for the flux control coefficients to yield

[math]\displaystyle{ C^J_{v_1} = \frac{\varepsilon^{2}_s}{\varepsilon^{2}_s - \varepsilon^{1}_s} }[/math]
[math]\displaystyle{ C^J_{v_2} = \frac{-\varepsilon^{1}_s}{\varepsilon^{2}_s - \varepsilon^{1}_s} }[/math]

Using these equations we can look at some simple extreme behaviors. For example, let us assume that the first step is completely insensitive to its product (i.e. not reacting with it), S, then [math]\displaystyle{ \varepsilon^{v_1}_s = 0 }[/math]. In this case, the control coefficients reduce to

[math]\displaystyle{ C^J_{v_1} = 1 }[/math]
[math]\displaystyle{ C^J_{v_2} = 0 }[/math]

That is all the control (or sensitivity) is on the first step. This situation represents the classic rate-limiting step that is frequently mentioned in textbooks. The flux through the pathway is completely dependent on the first step. Under these conditions, no other step in the pathway can affect the flux. The effect is however dependent on the complete insensitivity of the first step to its product. Such a situation is likely to be rare in real pathways. In fact the classic rate limiting step has almost never been observed experimentally. Instead, a range of limitingness is observed, with some steps having more limitingness (control) than others.

We can also derive the concentration control coefficients for the simple two step pathway:

[math]\displaystyle{ C^s_{v_1} = \frac{1}{\varepsilon^{2}_s - \varepsilon^1_s} }[/math]
[math]\displaystyle{ C^s_{v_2} = \frac{-1}{\varepsilon^{2}_s - \varepsilon^1_s} }[/math]

Three step pathway

Consider the simple three step pathway:

[math]\displaystyle{ X_o \rightarrow S_1 \rightarrow S_2 \rightarrow X_1 }[/math]

where [math]\displaystyle{ X_o }[/math] and [math]\displaystyle{ X_1 }[/math] are fixed boundary species, the control equations for this pathway can be derived in a similar manner to the simple two step pathway although it is somewhat more tedious.

[math]\displaystyle{ C^J_{e_1} = \varepsilon^{2}_1 \varepsilon^{3}_2 / D }[/math]
[math]\displaystyle{ C^J_{e_2} = -\varepsilon^{1}_1 \varepsilon^{3}_2 / D }[/math]
[math]\displaystyle{ C^J_{e_3} = \varepsilon^{1}_1 \varepsilon^{2}_2 / D }[/math]

where D the denominator is given by

[math]\displaystyle{ D = \varepsilon^{2}_1 \varepsilon^{3}_2 -\varepsilon^{1}_1 \varepsilon^{3}_2 + \varepsilon^{1}_1 \varepsilon^{2}_2 }[/math]

Note that every term in the numerator appears in the denominator, this ensures that the flux control coefficient summation theorem is satisfied.

Likewise the concentration control coefficients can also be derived, for [math]\displaystyle{ S_1 }[/math]

[math]\displaystyle{ C^{S_1}_{e_1} = (\varepsilon^{3}_2 - \varepsilon^{2}_2) / D }[/math]
[math]\displaystyle{ C^{S_1}_{e_2} = - \varepsilon^{3}_2 / D }[/math]
[math]\displaystyle{ C^{S_1}_{e_3} = \varepsilon^{2}_2 / D }[/math]

And for [math]\displaystyle{ S_2 }[/math]

[math]\displaystyle{ C^{S_2}_{e_1} = \varepsilon^{2}_1 / D }[/math]
[math]\displaystyle{ C^{S_2}_{e_2} = -\varepsilon^{1}_1 / D }[/math]
[math]\displaystyle{ C^{S_2}_{e_3} = (\varepsilon^{1}_1 - \varepsilon^{2}_1) / D }[/math]

Note that the denominators remain the same as before and behave as a normalizing factor.

Derivation using perturbations

Control equations can also be derived by considering the effect of perturbations on the system. Consider that reaction rates [math]\displaystyle{ v_1 }[/math] and [math]\displaystyle{ v_2 }[/math] are determined by two enzymes [math]\displaystyle{ e_1 }[/math] and [math]\displaystyle{ e_2 }[/math] respectively. Changing either enzyme will result in a change to the steady state level of [math]\displaystyle{ x }[/math] and the steady state reaction rates [math]\displaystyle{ v }[/math]. Consider a small change in [math]\displaystyle{ e_1 }[/math] of magnitude [math]\displaystyle{ \delta e_1 }[/math]. This will have a number of effects, it will increase [math]\displaystyle{ v_1 }[/math] which in turn will increase [math]\displaystyle{ x }[/math] which in turn will increase [math]\displaystyle{ v_2 }[/math]. Eventually the system will settle to a new steady state. We can describe these changes by focusing on the change in [math]\displaystyle{ v_1 }[/math] and [math]\displaystyle{ v_2 }[/math]. The change in [math]\displaystyle{ v_2 }[/math], which we designate [math]\displaystyle{ \delta v_2 }[/math], came about as a result of the change [math]\displaystyle{ \delta x }[/math]. Because we are only considering small changes we can express the change [math]\displaystyle{ \delta v_2 }[/math] in terms of [math]\displaystyle{ \delta x }[/math] using the relation

[math]\displaystyle{ \delta v_2 = \frac{\partial v_2}{\partial x} \delta x }[/math]

where the derivative [math]\displaystyle{ \partial v_2/\partial x }[/math] measures how responsive [math]\displaystyle{ v_2 }[/math] is to changes in [math]\displaystyle{ x }[/math]. The derivative can be computed if we know the rate law for [math]\displaystyle{ v_2 }[/math]. For example, if we assume that the rate law is [math]\displaystyle{ v_2 = k_2 x }[/math] then the derivative is [math]\displaystyle{ k_2 }[/math]. We can also use a similar strategy to compute the change in [math]\displaystyle{ v_1 }[/math] as a result of the change [math]\displaystyle{ \delta e_1 }[/math]. This time the change in [math]\displaystyle{ v_1 }[/math] is a result of two changes, the change in [math]\displaystyle{ e_1 }[/math] itself and the change in [math]\displaystyle{ x }[/math]. We can express these changes by summing the two individual contributions:

[math]\displaystyle{ \delta v_1 = \frac{\partial v_1}{\partial e_1} \delta e_1 + \frac{\partial v_1}{\partial x} \delta x }[/math]

We have two equations, one describing the change in [math]\displaystyle{ v_1 }[/math] and the other in [math]\displaystyle{ v_2 }[/math]. Because we allowed the system to settle to a new steady state we can also state that the change in reaction rates must be the same (otherwise it wouldn't be at steady state). That is we can assert that [math]\displaystyle{ \delta v_1 = \delta v_2 }[/math]. With this in mind we equate the two equations and write

[math]\displaystyle{ \frac{\partial v_2}{\partial x} \delta x = \frac{\partial v_1}{\partial e_1} \delta e_1 + \frac{\partial v_1}{\partial x} \delta x }[/math]

Solving for the ratio [math]\displaystyle{ \delta x/\delta e_1 }[/math] we obtain:

[math]\displaystyle{ \frac{\delta x}{\delta e_1} = \dfrac{-\dfrac{\partial v_1}{\partial e_1}}{\dfrac{\partial v_2}{\partial x} - \dfrac{\partial v_1}{\partial x}} }[/math]

In the limit, as we make the change [math]\displaystyle{ \delta e_1 }[/math] smaller and smaller, the left-hand side converges to the derivative [math]\displaystyle{ dx/de_1 }[/math]:

[math]\displaystyle{ \lim_{\delta e_1 \rightarrow 0} \frac{\delta x}{\delta e_1} = \frac{dx}{de_1} = \dfrac{-\dfrac{\partial v_1}{\partial e_1}}{\dfrac{\partial v_2}{\partial x} - \dfrac{\partial v_1}{\partial x}} }[/math]

We can go one step further and scale the derivatives to eliminate units. Multiplying both sides by [math]\displaystyle{ e_1 }[/math] and dividing both sides by [math]\displaystyle{ x }[/math] yields the scaled derivatives:

[math]\displaystyle{ \frac{dx}{de_1} \frac{e_1}{x}= \frac{-\dfrac{\partial v_1}{\partial e_1}\dfrac{e_1}{v_1}} {\dfrac{\partial v_2}{\partial x} \dfrac{x}{v_2} - \dfrac{\partial v_1}{\partial x} \dfrac{x}{v_1}} }[/math]

The scaled derivatives on the right-hand side are the elasticities, [math]\displaystyle{ \varepsilon^v_x }[/math] and the scaled left-hand term is the scaled sensitivity coefficient or concentration control coefficient, [math]\displaystyle{ C^x_{e} }[/math]

[math]\displaystyle{ C^x_{e_1} = \frac{\varepsilon^1_{e_1}}{\varepsilon^2_x - \varepsilon^1_x} }[/math]

We can simplify this expression further. The reaction rate [math]\displaystyle{ v_1 }[/math] is usually a linear function of [math]\displaystyle{ e_1 }[/math]. For example, in the Briggs–Haldane equation, the reaction rate is given by [math]\displaystyle{ v= e_1 k_{cat} x/(K_m + x) }[/math]. Differentiating this rate law with respect to [math]\displaystyle{ e_1 }[/math] and scaling yields [math]\displaystyle{ \varepsilon^{v_{1}}_{e_1} = 1 }[/math].

Using this result gives:

[math]\displaystyle{ C^x_{e_1} = \frac{1}{\varepsilon^2_x - \varepsilon^1_x} }[/math]

A similar analysis can be done where [math]\displaystyle{ e_2 }[/math] is perturbed. In this case we obtain the sensitivity of [math]\displaystyle{ x }[/math] with respect to [math]\displaystyle{ e_2 }[/math]:

[math]\displaystyle{ C^x_{e_2} = -\frac{1}{\varepsilon^2_x - \varepsilon^1_x} }[/math]

The above expressions measure how much enzymes [math]\displaystyle{ e_1 }[/math] and [math]\displaystyle{ e_2 }[/math] control the steady state concentration of intermediate [math]\displaystyle{ x }[/math]. We can also consider how the steady state reaction rates [math]\displaystyle{ v_1 }[/math] and [math]\displaystyle{ v_2 }[/math] are affected by perturbations in [math]\displaystyle{ e_1 }[/math] and [math]\displaystyle{ e_2 }[/math]. This is often of importance to metabolic engineers who are interested in increasing rates of production. At steady state the reaction rates are often called the fluxes and abbreviated to [math]\displaystyle{ J_1 }[/math] and [math]\displaystyle{ J_2 }[/math]. For a linear pathway such as this example, both fluxes are equal at steady-state so that the flux through the pathway is simply referred to as [math]\displaystyle{ J }[/math]. Expressing the change in flux as a result of a perturbation in [math]\displaystyle{ e_1 }[/math] and taking the limit as before we obtain

[math]\displaystyle{ C^J_{e_1} = \frac{\varepsilon^1_x}{\varepsilon^2_x - \varepsilon^1_x}, \quad C^J_{e_2} = \frac{-\varepsilon^1_x}{\varepsilon^2_x - \varepsilon^1_x} }[/math]

The above expressions tell us how much enzymes [math]\displaystyle{ e_1 }[/math] and [math]\displaystyle{ e_2 }[/math] control the steady state flux. The key point here is that changes in enzyme concentration, or equivalently the enzyme activity, must be brought about by an external action.

Derivation using the systems equation

The control equations can also be derived in a more rigorous fashion using the systems equation:

[math]\displaystyle{ \dfrac{{\bf dx}}{dt} = {\bf N} {\bf v} ({\bf x} (p), p) }[/math]

where [math]\displaystyle{ {\bf N} }[/math] is the stoichiometry matrix, [math]\displaystyle{ {\bf x} }[/math] is a vector of chemical species, and [math]\displaystyle{ {\bf p} }[/math] is a vector of parameters (or inputs) that can influence the system. In metabolic control analysis the key parameters are the enzyme concentrations. This approach was popularized by Heinrich, Rapoport, and Rapoport[16] and Reder and Mazat.[17] A detailed discussion of this approach can be found in Heinrich & Schuster[18] and Hofmeyr.[19]

Properties of a linear pathway

A linear biochemical pathway is a chain of enzyme-catalyzed reaction steps. The figure below shows a three step pathway, with intermediates, [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_2 }[/math]. In order to sustain a steady-state, the boundary species [math]\displaystyle{ X_o }[/math] and [math]\displaystyle{ X_1 }[/math] are fixed.

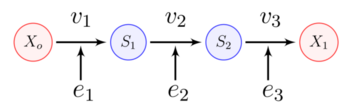
Linear chain of four reactions catalyzed by enzymes e1 to e4

At steady-state the rate of reaction is the same at each step. This means there is an overall flux from X_o to X_1.

Linear pathways possess some well-known properties:[20][21][22]

  1. Flux control is biased towards the first few steps of the pathway. Flux control shifts more to the first step as the equilibrium constants become large.
  2. Flux control is small at reactions close to equilibrium.
  3. Assuming reversibly, flux control at a given step is proportional to the product of the equilibrium constants. For example, flux control at the second step in a three step pathway is proportional to the product of the second and third equilibrium constants.

In all cases, a rationale for these behaviors is given in terms of how elasticities transmit changes through a pathway.

Metabolic control analysis software

There are a number of software tools that can directly compute elasticities and control coefficients:

Relationship to Classical Control Theory

Classical Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. In 2004 Brian Ingalls published a paper[26] that showed that classical control theory and metabolic control analysis were identical. The only difference was that metabolic control analysis was confined to zero frequency responses when cast in the frequency domain whereas classical control theory imposes no such restriction. The other significant difference is that classical control theory[27] has no notion of stoichiometry and conservation of mass which makes it more cumbersome to use but also means it fails to recognize the structural properties inherent in stoichiometric networks which provide useful biological insights.

See also

References

  1. ↑ Fell D., (1997) Understanding the Control of Metabolism, Portland Press.
  2. ↑ Heinrich R. and Schuster S. (1996) The Regulation of Cellular Systems, Chapman and Hall.
  3. ↑ Salter, M.; Knowles, R. G.; Pogson, C. I. (1994). "Metabolic control". Essays in Biochemistry 28: 1–12. PMID 7925313. 
  4. ↑ Ingalls, B. P. (2004) A Frequency Domain Approach to Sensitivity Analysis of Biochemical Systems, Journal of Physical Chemistry B, 108, 1143-1152.
  5. ↑ Savageau M.A (1976) Biochemical systems analysis: a study of function and design in molecular biology, Reading, MA, Addison–Wesley.
  6. ↑ Higgins, J. (1963). "Analysis of sequential reactions". Annals of the New York Academy of Sciences 108 (1): 305–321. doi:10.1111/j.1749-6632.1963.tb13382.x. PMID 13954410. Bibcode: 1963NYASA.108..305H. 
  7. ↑ Feinberg, Martin (1987). "Chemical reaction network structure and the stability of complex isothermal reactors—I. The deficiency zero and deficiency one theorems" (in en). Chemical Engineering Science 42 (10): 2229–2268. doi:10.1016/0009-2509(87)80099-4. https://linkinghub.elsevier.com/retrieve/pii/0009250987800994. 
  8. ↑ Clarke, Bruce L. (January 1980), Prigogine, I.; Rice, Stuart A., eds., "Stability of Complex Reaction Networks" (in en), Advances in Chemical Physics (Wiley) 43: pp. 1–215, doi:10.1002/9780470142622.ch1, ISBN 978-0-471-05741-3, https://onlinelibrary.wiley.com/doi/10.1002/9780470142622.ch1, retrieved 2023-12-06 
  9. ↑ Shinar, Guy; Alon, Uri; Feinberg, Martin (2009). "Sensitivity and Robustness in Chemical Reaction Networks". SIAM Journal on Applied Mathematics 69 (4): 977–998. ISSN 0036-1399. https://www.jstor.org/stable/40233656. 
  10. ↑ 10.0 10.1 10.2 10.3 Kacser, H.; Burns, J. A. (1973). "The control of flux". Symposia of the Society for Experimental Biology 27: 65–104. PMID 4148886. 
  11. ↑ 11.0 11.1 11.2 Heinrich, R.; Rapoport, T. A. (1974). "A linear steady-state treatment of enzymatic chains. General properties, control and effector strength". European Journal of Biochemistry 42 (1): 89–95. doi:10.1111/j.1432-1033.1974.tb03318.x. PMID 4830198. 
  12. ↑ Burns, J.A.; Cornish-Bowden, A.; Groen, A.K.; Heinrich, R.; Kacser, H.; Porteous, J.W.; Rapoport, S.M.; Rapoport, T.A. et al. (1985). "Control analysis of metabolic systems". Trends Biochem. Sci. 10: 16. doi:10.1016/0968-0004(85)90008-8. 
  13. ↑ Liebermeister, Wolfram (11 May 2022). "Structural Thermokinetic Modelling". Metabolites 12 (5): 434. doi:10.3390/metabo12050434. PMID 35629936. 
  14. ↑ Liebermeister, Wolfram (2016). Optimal enzyme rhythms in cells. 
  15. ↑ Moreno-Sánchez, Rafael; Saavedra, Emma; Rodríguez-Enríquez, Sara; Olín-Sandoval, Viridiana (2008). "Metabolic Control Analysis: A Tool for Designing Strategies to Manipulate Metabolic Pathways". Journal of Biomedicine and Biotechnology 2008: 1–30. doi:10.1155/2008/597913. PMID 18629230. 
  16. ↑ Heinrich, R.; Rapoport, S. M.; Rapoport, T. A. (1 January 1978). "Metabolic regulation and mathematical models". Progress in Biophysics and Molecular Biology 32 (1): 1–82. doi:10.1016/0079-6107(78)90017-2. PMID 343173. 
  17. ↑ Reder, Christine (November 1988). "Metabolic control theory: A structural approach". Journal of Theoretical Biology 135 (2): 175–201. doi:10.1016/S0022-5193(88)80073-0. PMID 3267767. Bibcode: 1988JThBi.135..175R. 
  18. ↑ Heinrich, Reinhart; Schuster, Stefan (1996). "The Regulation of Cellular Systems" (in en). SpringerLink. doi:10.1007/978-1-4613-1161-4. ISBN 978-1-4612-8492-5. https://link.springer.com/book/10.1007/978-1-4613-1161-4. 
  19. ↑ Hofmeyr, Jan-Hendrik. "Metabolic control analysis in a nutshell". Proceedings of the 2nd International Conference on Systems Biology. https://www.academia.edu/4610732. 
  20. ↑ Heinrich, Reinhart; Rapoport, Tom A. (February 1974). "A Linear Steady-State Treatment of Enzymatic Chains. General Properties, Control and Effector Strength". European Journal of Biochemistry 42 (1): 89–95. doi:10.1111/j.1432-1033.1974.tb03318.x. 
  21. ↑ Savageau, Michael (1976). Biochemical systems analysis. A study of function and design in molecular biology.. Addison-Wesley. 
  22. ↑ Sauro, Herbert (28 August 2020). "A brief note on the properties of linear pathways". Biochemical Society Transactions 48 (4): 1379–1395. doi:10.1042/BST20190842. 
  23. ↑ Olivier, B. G.; Rohwer, J. M.; Hofmeyr, J.-H. S. (15 February 2005). "Modelling cellular systems with PySCeS". Bioinformatics 21 (4): 560–561. doi:10.1093/bioinformatics/bti046. PMID 15454409. 
  24. ↑ Bergmann, Frank T.; Sauro, Herbert M. (December 2006). "SBW - A Modular Framework for Systems Biology". Proceedings of the 2006 Winter Simulation Conference. pp. 1637–1645. doi:10.1109/WSC.2006.322938. ISBN 1-4244-0501-7. 
  25. ↑ Choi, Kiri; Medley, J. Kyle; König, Matthias; Stocking, Kaylene; Smith, Lucian; Gu, Stanley; Sauro, Herbert M. (September 2018). "Tellurium: An extensible python-based modeling environment for systems and synthetic biology". Biosystems 171: 74–79. doi:10.1016/j.biosystems.2018.07.006. PMID 30053414. 
  26. ↑ Drengstig, Tormod; Kjosmoen, Thomas; Ruoff, Peter (19 May 2011). "On the Relationship between Sensitivity Coefficients and Transfer Functions of Reaction Kinetic Networks". The Journal of Physical Chemistry B 115 (19): 6272–6278. doi:10.1021/jp200578e. PMID 21520979. 
  27. ↑ Nise, Norman S. (2019). Control systems engineering (Eighth, Wiley abridged print companion ed.). Hoboken, NJ. ISBN 978-1119592921. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Biology:Metabolic_control_analysis&oldid=3558143"