Bivariegated graph

In graph theory, a bivariegated graph is a graph whose vertex set can be partitioned into two equal parts such that each vertex is adjacent to exactly one vertex from the other set not containing it. In a bivarigated graph G with 2n vertices, there exists a set of n independent edges such that no odd number of them lie on a cycle of G.

Examples

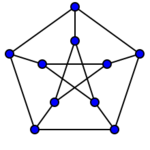
The Petersen graph, shown below, is a bivariegated graph: if one partitions it into an outer pentagon and an inner five-point star, each vertex on one side of the partition has exactly one neighbor on the other side of the partition. More generally, the same is true for any generalized Petersen graph formed by connecting an outer polygon and an inner star with the same number of points; for instance, this applies to the Möbius–Kantor graph and the Desargues graph.

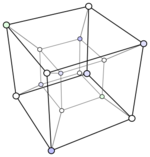
Any hypercube graph, such as the four-dimensional hypercube shown below, is also bivariegated.

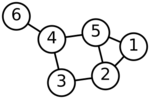
However, the graph shown below is not bivariegated. Whatever you choose the three independent edges, one of them is an edge of a cycle.

Bivariegated trees

A tree T with 2n vertices, is bivariegated if and only if the independence number of T is n, or, equivalently, if and only if it has a perfect matching.

Generalizations

The k-varigated graph, k ≥ 3, can be defined similarly. A graph is said to be k-varigated if its vertex set can be partitioned into k equal parts such that each vertex is adjacent to exactly one vertex from every other part not containing it.

Notes

• Characterizing the degree sequences of bivariegated graphs has been an unsolved problem in graph theory.

References

• Bednarek, A. R.; Sanders, E. L. (1973), "A characterization of bivariegated trees", Discrete Mathematics 5: 1–14, doi:10.1016/0012-365X(73)90022-8 .
• Bhat-Nayak, Vasanti N.; Choudum, S. A.; Naik, Ranjan N. (1978), "Characterization of 2-variegated graphs and of 3-variegated graphs", Discrete Mathematics 23: 17–22, doi:10.1016/0012-365X(78)90182-6 .
• Bhat-Nayak, Vasanti N.; Kocay, W. L.; Naik, Ranjan N. (1980), "Forcibly 2-variegated degree sequences", Utilitas Math. 18: 83–89 .
• Bhat-Nayak Vasanti N., Ranjan N. Naik, Further results on 2-variegated graphs, Utilitas Math. 12 (1977) 317–325.
• Javdekar, Medha (1980), "Characterization of forcibly k-variegated degree sequences, k ≥ 3", Discrete Mathematics 29 (1): 33–38, doi:10.1016/0012-365X(90)90284-O .
• Javdekar, Medha (1980), "Characterization of k-variegated graphs, k ≥ 3", Discrete Mathematics 32 (3): 263–270, doi:10.1016/0012-365X(80)90264-2 
• Riddle, Fay A. (1978), Bivariegated Graphs and Their Isomorphisms, Ph.D. dissertation, University of Florida .