Brjuno number
In mathematics, a Brjuno number (sometimes spelled Bruno or Bryuno) is a special type of irrational number named for Russian mathematician Alexander Bruno, who introduced them in (Brjuno 1971).
Formal definition
An irrational number [math]\displaystyle{ \alpha }[/math] is called a Brjuno number when the infinite sum
- [math]\displaystyle{ B(\alpha) = \sum_{n=0}^\infty \frac{\log q_{n+1}}{q_n} }[/math]
converges to a finite number.
Here:
- [math]\displaystyle{ q_n }[/math] is the denominator of the nth convergent [math]\displaystyle{ \tfrac{p_n}{q_n} }[/math] of the continued fraction expansion of [math]\displaystyle{ \alpha }[/math].
- [math]\displaystyle{ B }[/math] is a Brjuno function
Importance
The Brjuno numbers are important in the one–dimensional analytic small divisors problems. Bruno improved the diophantine condition in Siegel's Theorem, showed that germs of holomorphic functions with linear part [math]\displaystyle{ e^{2\pi i \alpha} }[/math] are linearizable if [math]\displaystyle{ \alpha }[/math] is a Brjuno number. Jean-Christophe Yoccoz (1995) showed in 1987 that this condition is also necessary, and for quadratic polynomials is necessary and sufficient.
Properties
Intuitively, these numbers do not have many large "jumps" in the sequence of convergents, in which the denominator of the (n + 1)th convergent is exponentially larger than that of the nth convergent. Thus, in contrast to the Liouville numbers, they do not have unusually accurate diophantine approximations by rational numbers.
Brjuno function
Brjuno sum
The Brjuno sum or Brjuno function [math]\displaystyle{ B }[/math] is
- [math]\displaystyle{ B(\alpha) = \sum_{n=0}^\infty \frac{\log q_{n+1}}{q_n} }[/math]
where:
- [math]\displaystyle{ q_n }[/math] is the denominator of the nth convergent [math]\displaystyle{ \tfrac{p_n}{q_n} }[/math] of the continued fraction expansion of [math]\displaystyle{ \alpha }[/math].
Real variant
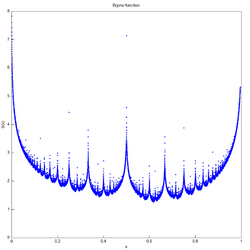
The real Brjuno function [math]\displaystyle{ B(\alpha) }[/math] is defined for irrational numbers [math]\displaystyle{ \alpha }[/math] [1]
- [math]\displaystyle{ B : \R \setminus \Q \to \R \cup \{ +\infty \} }[/math]
and satisfies
- [math]\displaystyle{ \begin{align} B(\alpha) &= B(\alpha+1) \\ B(\alpha) &= - \log \alpha + \alpha B(1/\alpha) \end{align} }[/math]
for all irrational [math]\displaystyle{ \alpha }[/math] between 0 and 1.
Yoccoz's variant
Yoccoz's variant of the Brjuno sum defined as follows:[2]
- [math]\displaystyle{ Y(\alpha)=\sum_{n=0}^{\infty} \alpha_0\cdots \alpha_{n-1} \log \frac{1}{\alpha_n}, }[/math]
where:
- [math]\displaystyle{ \alpha }[/math] is irrational real number: [math]\displaystyle{ \alpha\in \R \setminus \Q }[/math]
- [math]\displaystyle{ \alpha_0 }[/math] is the fractional part of [math]\displaystyle{ \alpha }[/math]
- [math]\displaystyle{ \alpha_{n+1} }[/math] is the fractional part of [math]\displaystyle{ \frac{1}{\alpha_n} }[/math]
This sum converges if and only if the Brjuno sum does, and in fact their difference is bounded by a universal constant.
See also
References
- Brjuno, Alexander D. (1971), "Analytic form of differential equations. I, II", Trudy Moskovskogo Matematičeskogo Obščestva 25: 119–262, ISSN 0134-8663
- Lee, Eileen F. (Spring 1999), "The structure and topology of the Brjuno numbers", Proceedings of the 1999 Topology and Dynamics Conference (Salt Lake City, UT), Topology Proceedings, 24, pp. 189–201, http://topology.nipissingu.ca/tp/reprints/v24/tp24114.pdf
- Marmi, Stefano; Moussa, Pierre; Yoccoz, Jean-Christophe (2001), "Complex Brjuno functions", Journal of the American Mathematical Society 14 (4): 783–841, doi:10.1090/S0894-0347-01-00371-X, ISSN 0894-0347
- "Théorème de Siegel, nombres de Bruno et polynômes quadratiques", Petits diviseurs en dimension 1, Astérisque, 231, 1995, pp. 3–88
Notes
 |  |
