Broadcast (parallel pattern)
Broadcast is a collective communication primitive in parallel programming to distribute programming instructions or data to nodes in a cluster. It is the reverse operation of reduction.[1] The broadcast operation is widely used in parallel algorithms, such as matrix-vector multiplication,[1] Gaussian elimination and shortest paths.[2]
The Message Passing Interface implements broadcast in MPI_Bcast.[3]
Definition
A message [math]\displaystyle{ M [1 .. m] }[/math]of length [math]\displaystyle{ m }[/math] should be distributed from one node to all other [math]\displaystyle{ p-1 }[/math] nodes.
[math]\displaystyle{ T_\text{byte} }[/math]is the time it takes to send one byte.
[math]\displaystyle{ T_\text{start} }[/math]is the time it takes for a message to travel to another node, independent of its length.
Therefore, the time to send a package from one node to another is [math]\displaystyle{ t = \mathrm{size} \times T_\text{byte} + T_\text{start} }[/math].[1]
[math]\displaystyle{ p }[/math] is the number of nodes and the number of processors.
Binomial Tree Broadcast
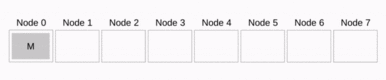
With Binomial Tree Broadcast the whole message is sent at once. Each node that has already received the message sends it on further. This grows exponentially as each time step the amount of sending nodes is doubled. The algorithm is ideal for short messages but falls short with longer ones as during the time when the first transfer happens only one node is busy.
Sending a message to all nodes takes [math]\displaystyle{ \log_2(p) t }[/math] time which results in a runtime of [math]\displaystyle{ \log_2(p) ( m T_\text{byte} + T_\text{start}) }[/math]
Message M
id := node number
p := number of nodes
if id > 0
blocking_receive M
for (i := ceil(log_2(p)) - 1; i >= 0; i--)
if (id % 2^(i+1) == 0 && id + 2^i <= p)
send M to node id + 2^i
Linear Pipeline Broadcast
The message is split up into [math]\displaystyle{ k }[/math] packages and send piecewise from node [math]\displaystyle{ n }[/math] to node [math]\displaystyle{ n+1 }[/math]. The time needed to distribute the first message piece is [math]\displaystyle{ p t = \frac{m}{k} T_\text{byte} + T_\text{start} }[/math] whereby [math]\displaystyle{ t }[/math] is the time needed to send a package from one processor to another.
Sending a whole message takes [math]\displaystyle{ ( p + k )\left( \frac{mT_\text{byte}}{k} + T_\text{start} \right) = (p + k) t = p t + k t }[/math].
Optimal is to choose [math]\displaystyle{ k = \sqrt{ \frac{ m (p-2) T_\text{byte} }{T_\text{start} } } }[/math] resulting in a runtime of approximately [math]\displaystyle{ m T_\text{byte} + p T_\text{start} + \sqrt{m p T_\text{start} T_\text{byte}} }[/math]
The run time is dependent on not only message length but also the number of processors that play roles. This approach shines when the length of the message is much larger than the amount of processors.
Message M := [m_1, m_2, ..., m_n]
id = node number
for (i := 1; i <= n; i++) in parallel
if (id != 0)
blocking_receive m_i
if (id != n)
send m_i to node id + 1
Pipelined Binary Tree Broadcast
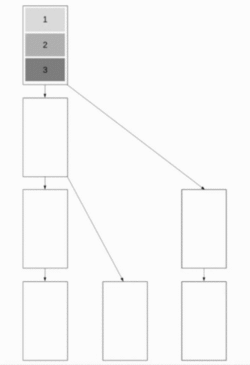
This algorithm combines Binomial Tree Broadcast and Linear Pipeline Broadcast, which makes the algorithm work well for both short and long messages. The aim is to have as many nodes work as possible while maintaining the ability to send short messages quickly. A good approach is to use Fibonacci trees for splitting up the tree, which are a good choice as a message cannot be sent to both children at the same time. This results in a binary tree structure.
We will assume in the following that communication is full-duplex. The Fibonacci tree structure has a depth of about [math]\displaystyle{ d \approx \log_\Phi(p) }[/math]whereby [math]\displaystyle{ \Phi = \frac{1+\sqrt{5}}{2} }[/math]the golden ratio.
The resulting runtime is [math]\displaystyle{ (\frac{m}{k}T_\text{byte} + T_\text{start})(d + 2k - 2) }[/math]. Optimal is [math]\displaystyle{ k = \sqrt{\frac{n (d-2) T_\text{byte} }{ 3T_\text{start}}} }[/math].
This results in a runtime of [math]\displaystyle{ 2mT_\text{byte} + T_\text{start} \log_\Phi(p) + \sqrt{2m \log_\Phi(p) T_\text{start} T_\text{byte}} }[/math].
Message M := [m_1, m_2, ..., m_k]
for i = 1 to k
if (hasParent())
blocking_receive m_i
if (hasChild(left_child))
send m_i to left_child
if (hasChild(right_child))
send m_i to right_child
Two Tree Broadcast (23-Broadcast)
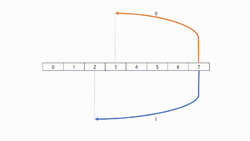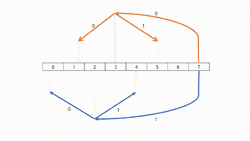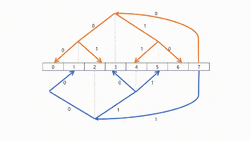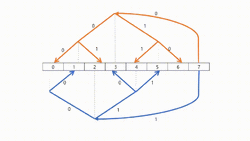
Definition
This algorithm aims to improve on some disadvantages of tree structure models with pipelines. Normally in tree structure models with pipelines (see above methods), leaves receive just their data and cannot contribute to send and spread data.
The algorithm concurrently uses two binary trees to communicate over. Those trees will be called tree A and B. Structurally in binary trees there are relatively more leave nodes than inner nodes. Basic Idea of this algorithm is to make a leaf node of tree A be an inner node of tree B. It has also the same technical function in opposite side from B to A tree. This means, two packets are sent and received by inner nodes and leaves in different steps.
Tree construction
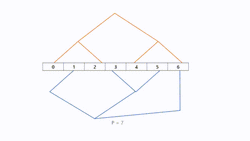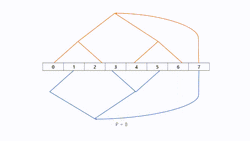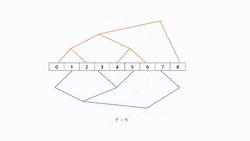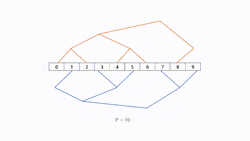
The number of steps needed to construct two parallel-working binary trees is dependent on the amount of processors. Like with other structures one processor can is the root node who sends messages to two trees. It is not necessary to set a root node, because it is not hard to recognize that the direction of sending messages in binary tree is normally top to bottom. There is no limitation on the number of processors to build two binary trees. Let the height of the combined tree be h = ⌈log(p + 2)⌉. Tree A and B can have a height of [math]\displaystyle{ h -1 }[/math]. Especially, if the number of processors correspond to [math]\displaystyle{ p = 2^h - 1 }[/math], we can make both sides trees and a root node.
To construct this model efficiently and easily with a fully built tree, we can use two methods called "Shifting" and "Mirroring" to get second tree. Let assume tree A is already modeled and tree B is supposed to be constructed based on tree A. We assume that we have [math]\displaystyle{ p }[/math] processors ordered from 0 to [math]\displaystyle{ p-1 }[/math].
Shifting
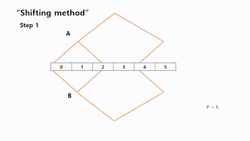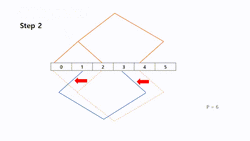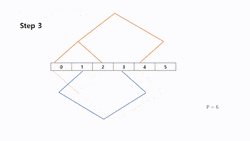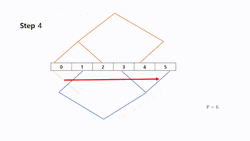
The "Shifting" method, first copies tree A and moves every node one position to the left to get tree B. The node, which will be located on -1, becomes a child of processor [math]\displaystyle{ p-2 }[/math].
Mirroring
"Mirroring" is ideal for an even number of processors. With this method tree B can be more easily constructed by tree A, because there are no structural transformations in order to create the new tree. In addition, a symmetric process makes this approach simple. This method can also handle an odd number of processors, in this case, we can set processor [math]\displaystyle{ p-1 }[/math] as root node for both trees. For the remaining processors "Mirroring" can be used.
Coloring
We need to find a schedule in order to make sure that no processor has to send or receive two messages from two trees in a step. The edge, is a communication connection to connect two nodes, and can be labelled as either 0 or 1 to make sure that every processor can alternate between 0 and 1-labelled edges. The edges of A and B can be colored with two colors (0 and 1) such that
- no processor is connected to its parent nodes in A and B using edges of the same color-
- no processor is connected to its children nodes in A or B using edges of the same color.[7]
In every even step the edges with 0 are activated and edges with 1 are activated in every odd step.
Time complexity
In this case the number of packet k is divided in half for each tree. Both trees are working together the total number of packets [math]\displaystyle{ k = k/2 + k/2 }[/math] (upper tree + bottom tree)
In each binary tree sending a message to another nodes takes [math]\displaystyle{ 2i }[/math] steps until a processor has at least a packet in step [math]\displaystyle{ i }[/math]. Therefore, we can calculate all steps as [math]\displaystyle{ d := \log_2 (p+1) \Rightarrow \log_2(p+1) \approx \log_2(p) }[/math].
The resulting run time is [math]\displaystyle{ T(m,p,k) \approx (\frac{m}{k}T_\text{byte} + T_\text{start})(2d + k - 1) }[/math]. (Optimal [math]\displaystyle{ k = \sqrt{{m (2d-1) T_\text{byte} }/{ T_\text{start}}} }[/math])
This results in a run time of [math]\displaystyle{ T(m,p) \approx mT_\text{byte} + T_\text{start} \cdot 2\log_2 (p) + \sqrt{m \cdot 2\log_2 (p) T_\text{start} T_\text{byte}} }[/math].
ESBT-Broadcasting (Edge-disjoint Spanning Binomial Trees)
In this section, another broadcasting algorithm with an underlying telephone communication model will be introduced. A Hypercube creates network system with [math]\displaystyle{ p = 2^d (d = 0,1,2,3,...) }[/math]. Every node is represented by binary [math]\displaystyle{ {0,1} }[/math] depending on the number of dimensions. Fundamentally ESBT(Edge-disjoint Spanning Binomial Trees) is based on hypercube graphs, pipelining([math]\displaystyle{ m }[/math] messages are divided by [math]\displaystyle{ k }[/math] packets) and binomial trees. The Processor [math]\displaystyle{ 0^d }[/math] cyclically spreads packets to roots of ESBTs. The roots of ESBTs broadcast data with binomial tree. To leave all of [math]\displaystyle{ k }[/math] from [math]\displaystyle{ p_0 }[/math], [math]\displaystyle{ k }[/math] steps are required, because all packets are distributed by [math]\displaystyle{ p_0 }[/math]. It takes another d steps until the last leaf node receives the packet. In total [math]\displaystyle{ d+ k }[/math] steps are necessary to broadcast [math]\displaystyle{ m }[/math] message through ESBT.
The resulting run time is [math]\displaystyle{ T(m,p,k) = (\frac{m}{k}T_\text{byte} + T_\text{start})(k+d) }[/math]. [math]\displaystyle{ (k = \sqrt{{m d T_\text{byte} }/{ T_\text{start}}}) }[/math].
This results in a run time of [math]\displaystyle{ T(m,p) := mT_\text{byte} + dT_\text{start} + \sqrt{mdT_\text{start} T_\text{byte}} }[/math].
See also
References
- ↑ 1.0 1.1 1.2 Kumar, Vipin (2002). Introduction to Parallel Computing (2nd ed.). Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc.. pp. 185, 151, 66. ISBN 9780201648652. https://dl.acm.org/citation.cfm?id=600009.
- ↑ 2.0 2.1 Bruck, J.; Cypher, R.; Ho, C-T. (1992). "Multiple message broadcasting with generalized Fibonacci trees". [1992] Proceedings of the Fourth IEEE Symposium on Parallel and Distributed Processing. pp. 424–431. doi:10.1109/SPDP.1992.242714. ISBN 0-8186-3200-3. https://authors.library.caltech.edu/12404/.
- ↑ MPI: A Message-Passing Interface StandardVersion 3.0, Message Passing Interface Forum, pp. 148, 2012
- ↑ 4.0 4.1 4.2 Michael Ikkert, T. Kieritz, P. Sanders Parralele Algorithme - Script (German), Karlsruhe Institute of Technology, pp. 29-32, 2009
- ↑ Michael Ikkert, T. Kieritz, P. Sanders Parralele Algorithme - Script (German), Karlsruhe Institute of Technology, pp.33-37, 2009
- ↑ P. Sanders [1] (German), Karlsruhe Institute of Technology, pp. 82-96, 2018
- ↑ 7.0 7.1 Sanders, Peter; Speck, Jochen; Träff, Jesper Larsson (2009). "Two-tree algorithms for full bandwidth broadcast, reduction and scan". Parallel Computing 35 (12): 581–594. doi:10.1016/j.parco.2009.09.001. ISSN 0167-8191.
- ↑ Michael Ikkert, T. Kieritz, P. Sanders Parralele Algorithme - Script (German), Karlsruhe Institute of Technology, pp.40-42, 2009
- ↑ P. Sanders [2] (German), Karlsruhe Institute of Technology, pp. 101-104, 2018
 |  |
