Broken diagonal
In recreational mathematics and the theory of magic squares, a broken diagonal is a set of n cells forming two parallel diagonal lines in the square. Alternatively, these two lines can be thought of as wrapping around the boundaries of the square to form a single sequence.
In pandiagonal magic squares
A magic square in which the broken diagonals have the same sum as the rows, columns, and diagonals is called a pandiagonal magic square.[1][2]
Examples of broken diagonals from the number square in the image are as follows: 3,12,14,5; 10,1,7,16; 10,13,7,4; 15,8,2,9; 15,12,2,5; and 6,13,11,4.
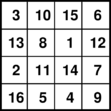
The fact that this square is a pandiagonal magic square can be verified by checking that all of its broken diagonals add up to the same constant:
- 3+12+14+5 = 34
- 10+1+7+16 = 34
- 10+13+7+4 = 34
One way to visualize a broken diagonal is to imagine a "ghost image" of the panmagic square adjacent to the original:
The set of numbers {3, 12, 14, 5} of a broken diagonal, wrapped around the original square, can be seen starting with the first square of the ghost image and moving down to the left.
In linear algebra
Broken diagonals are used in a formula to find the determinant of 3 by 3 matrices.
For a 3 × 3 matrix A, its determinant is
- [math]\displaystyle{ \begin{align} |A| = \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} &= a\,\begin{vmatrix} \Box & \Box & \Box \\ \Box & e & f \\ \Box & h & i \end{vmatrix} - b\,\begin{vmatrix} \Box & \Box & \Box \\ d & \Box & f \\ g & \Box & i \end{vmatrix} + c\,\begin{vmatrix} \Box & \Box & \Box \\ d & e & \Box \\ g & h & \Box \end{vmatrix} \\[3pt] &= a\,\begin{vmatrix} e & f \\ h & i \end{vmatrix} - b\,\begin{vmatrix} d & f \\ g & i \end{vmatrix} + c\,\begin{vmatrix} d & e \\ g & h \end{vmatrix} \\[3pt] &= aei + bfg + cdh - ceg - bdi - afh. \end{align} }[/math][3]
Here, [math]\displaystyle{ bfg, cdh, bdi, }[/math] and [math]\displaystyle{ afh }[/math] are (products of the elements of) the broken diagonals of the matrix.
Broken diagonals are used in the calculation of the determinants of all matrices of size 3 × 3 or larger. This can be shown by using the matrix's minors to calculate the determinant.
References
- ↑ Pickover, Clifford A. (2011), The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures across the Dimensions, Princeton University Press, p. 7, ISBN 9781400841516, https://books.google.com/books?id=-mu8O8RMG6QC&pg=PA7.
- ↑ Licks, H. E. (1921), Recreations in Mathematics, D. Van Nostrand Company, p. 42, https://books.google.com/books?id=MWcxAQAAMAAJ&pg=PA42.
- ↑ title=Determinant|url=https://mathworld.wolfram.com/Determinant.html
 |  |
