Bull graph
| Bull graph | |
|---|---|
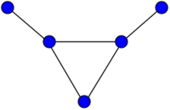 The bull graph | |
| Vertices | 5 |
| Edges | 5 |
| Radius | 2 |
| Diameter | 3 |
| Girth | 3 |
| Automorphisms | 2 (Z/2Z) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Planar Unit distance |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the bull graph is a planar undirected graph with 5 vertices and 5 edges, in the form of a triangle with two disjoint pendant edges.[1]
It has chromatic number 3, chromatic index 3, radius 2, diameter 3 and girth 3. It is also a self-complementary graph, a block graph, a split graph, an interval graph, a claw-free graph, a 1-vertex-connected graph and a 1-edge-connected graph.
Bull-free graphs
A graph is bull-free if it has no bull as an induced subgraph. The triangle-free graphs are bull-free graphs, since every bull contains a triangle. The strong perfect graph theorem was proven for bull-free graphs long before its proof for general graphs,[2] and a polynomial time recognition algorithm for Bull-free perfect graphs is known.[3]
Maria Chudnovsky and Shmuel Safra have studied bull-free graphs more generally, showing that any such graph must have either a large clique or a large independent set (that is, the Erdős–Hajnal conjecture holds for the bull graph),[4] and developing a general structure theory for these graphs.[5][6][7]
Chromatic and characteristic polynomial
The chromatic polynomial of the bull graph is [math]\displaystyle{ (x-2)(x-1)^3x }[/math]. Two other graphs are chromatically equivalent to the bull graph.
Its characteristic polynomial is [math]\displaystyle{ -x(x^2-x-3)(x^2+x-1) }[/math].
Its Tutte polynomial is [math]\displaystyle{ x^4+x^3+x^2y }[/math].
References
- ↑ Weisstein, Eric W.. "Bull Graph". http://mathworld.wolfram.com/BullGraph.html.
- ↑ Chvátal, V.; Sbihi, N. (1987), "Bull-free Berge graphs are perfect", Graphs and Combinatorics 3 (1): 127–139, doi:10.1007/BF01788536.
- ↑ Reed, B.; Sbihi, N. (1995), "Recognizing bull-free perfect graphs", Graphs and Combinatorics 11 (2): 171–178, doi:10.1007/BF01929485.
- ↑ Chudnovsky, M.; Safra, S. (2008), "The Erdős–Hajnal conjecture for bull-free graphs", Journal of Combinatorial Theory, Series B 98 (6): 1301–1310, doi:10.1016/j.jctb.2008.02.005.
- ↑ Chudnovsky, M. (2008), The structure of bull-free graphs. I. Three-edge paths with centers and anticenters, http://www.columbia.edu/~mc2775/bulls1.pdf.
- ↑ Chudnovsky, M. (2008), The structure of bull-free graphs. II. Elementary trigraphs, http://www.columbia.edu/~mc2775/bulls2.pdf.
- ↑ Chudnovsky, M. (2008), The structure of bull-free graphs. III. Global structure, http://www.columbia.edu/~mc2775/bulls3.pdf.
 |  |
