CUSUM

Short description: Sequential analysis technique

CUSUM chart
Originally proposed by	E. S. Page
Process observations
Rational subgroup size	n = 1
Measurement type	Cumulative sum of a quality characteristic
Quality characteristic type	Variables data
Underlying distribution	Normal distribution
Performance
Size of shift to detect	≤ 1.5σ
Process variation chart
Not applicable
Process mean chart
Center line	The target value, T, of the quality characteristic
Upper control limit	[math]\displaystyle{ C_i^+ = \max \lbrack 0, x_i - \left ( T + K \right ) + C_{i - 1}^+\rbrack }[/math]
Lower control limit	[math]\displaystyle{ C_i^- = \max \lbrack 0, \left ( T - K \right ) - x_i + C_{i - 1}^-\rbrack }[/math]
Plotted statistic	[math]\displaystyle{ C_i = \sum_{j=1}^i \bar x_j - T }[/math]

In statistical quality control, the CUSUM (or cumulative sum control chart) is a sequential analysis technique developed by E. S. Page of the University of Cambridge. It is typically used for monitoring change detection. CUSUM was announced in Biometrika, in 1954, a few years after the publication of Wald's sequential probability ratio test (SPRT).

E. S. Page referred to a "quality number" [math]\displaystyle{ \theta }[/math], by which he meant a parameter of the probability distribution; for example, the mean. He devised CUSUM as a method to determine changes in it, and proposed a criterion for deciding when to take corrective action. When the CUSUM method is applied to changes in mean, it can be used for step detection of a time series.

A few years later, George Alfred Barnard developed a visualization method, the V-mask chart, to detect both increases and decreases in [math]\displaystyle{ \theta }[/math].

Method

As its name implies, CUSUM involves the calculation of a cumulative sum (which is what makes it "sequential"). Samples from a process [math]\displaystyle{ x_n }[/math] are assigned weights [math]\displaystyle{ \omega_n }[/math], and summed as follows:

[math]\displaystyle{ S_0=0 }[/math]

[math]\displaystyle{ S_{n+1}=\max(0, S_n+x_{n+1}-\omega_n) }[/math]

When the value of S exceeds a certain threshold value, a change in value has been found. The above formula only detects changes in the positive direction. When negative changes need to be found as well, the min operation should be used instead of the max operation, and this time a change has been found when the value of S is below the (negative) value of the threshold value.

Page did not explicitly say that [math]\displaystyle{ \omega }[/math] represents the likelihood function, but this is common usage.

Note that this differs from SPRT by always using zero function as the lower "holding barrier" rather than a lower "holding barrier". Also, CUSUM does not require the use of the likelihood function.

As a means of assessing CUSUM's performance, Page defined the average run length (A.R.L.) metric; "the expected number of articles sampled before action is taken." He further wrote:

When the quality of the output is satisfactory the A.R.L. is a measure of the expense incurred by the scheme when it gives false alarms, i.e., Type I errors (Neyman & Pearson, 1936). On the other hand, for constant poor quality the A.R.L. measures the delay and thus the amount of scrap produced before the rectifying action is taken, i.e., Type II errors.

Example

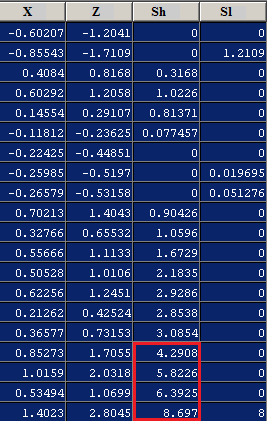
The following example shows 20 observations [math]\displaystyle{ X }[/math] of a process with a mean of 0 and a standard deviation of 0.5.

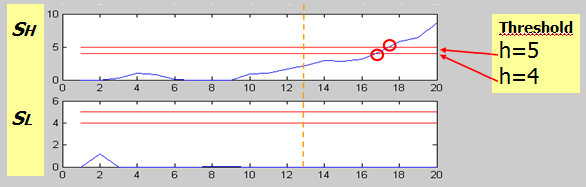
From the [math]\displaystyle{ Z }[/math] column, it can be seen that [math]\displaystyle{ X }[/math] never deviates by 3 standard deviations ([math]\displaystyle{ 3 \sigma }[/math]), so simply alerting on a high deviation will not detect a failure, whereas CUSUM shows that the [math]\displaystyle{ S_H }[/math] value exceeds 4 at the 17th observation.

Column	Description
[math]\displaystyle{ X }[/math]	The observations of the process with an expected mean [math]\displaystyle{ \bar{x} }[/math] of 0 and an expected standard deviation [math]\displaystyle{ \sigma_X }[/math] of 0.5
[math]\displaystyle{ Z }[/math]	The normalized observations, i.e. centered around the mean and scaled by the standard deviation [math]\displaystyle{ Z_n = \frac{X_n - \bar{x}}{\sigma_X} }[/math]
[math]\displaystyle{ S_H }[/math]	The high CUSUM value, detecting a positive anomaly, [math]\displaystyle{ {S_H}_{n+1} = \max(0, {S_H}_n + Z_{n+1} - \omega) }[/math]
[math]\displaystyle{ S_L }[/math]	The low CUSUM value, detecting a negative anomaly, [math]\displaystyle{ {S_L}_{n+1} = \max(0, {S_L}_n - Z_{n+1} - \omega) }[/math]

where [math]\displaystyle{ \omega }[/math] is a critical level parameter (tunable, same as threshold T) that's used to adjust the sensitivity of change detection: larger [math]\displaystyle{ \omega }[/math] makes CUSUM less sensitive to the change and vice versa.

Variants

Cumulative observed-minus-expected plots are a related method.

Further reading

• Michèle Basseville and Igor V. Nikiforov (April 1993). Detection of Abrupt Changes: Theory and Application. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0-13-126780-9. http://www.irisa.fr/sisthem/kniga/. 
• Mishra, S., Vanli, O. A., & Park, C (2015). "A Multivariate Cumulative Sum Method for Continuous Damage Monitoring with Lamb-wave Sensors", International Journal of Prognostics and Health Management, ISSN 2153-2648

External links

• "Engineering Statistics Handbook - Cusum Control Charts"