Carnot's theorem (inradius, circumradius)
From HandWiki
Short description: Gives the sum of the distances from the circumcenter to the sides of an arbitrary triangle
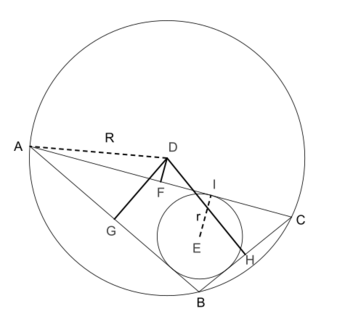
In Euclidean geometry, Carnot's theorem states that the sum of the signed distances from the circumcenter D to the sides of an arbitrary triangle ABC is
where r is the inradius and R is the circumradius of the triangle. Here the sign of the distances is taken to be negative if and only if the open line segment DX (X = F, G, H) lies completely outside the triangle. In the diagram, DF is negative and both DG and DH are positive.
The theorem is named after Lazare Carnot (1753–1823). It is used in a proof of the Japanese theorem for concyclic polygons.
References
- Claudi Alsina, Roger B. Nelsen: When Less is More: Visualizing Basic Inequalities. MAA, 2009, ISBN:978-0-88385-342-9, p.99
- Frédéric Perrier: Carnot's Theorem in Trigonometric Disguise. The Mathematical Gazette, Volume 91, No. 520 (March, 2007), pp. 115–117 (JSTOR)
- David Richeson: The Japanese Theorem for Nonconvex Polygons – Carnot's Theorem. Convergence, December 2013
External links
- Weisstein, Eric W.. "Carnot's theorem". http://mathworld.wolfram.com/CarnotsTheorem.html.
- Carnot's Theorem at cut-the-knot
- Carnot's Theorem by Chris Boucher. The Wolfram Demonstrations Project.

