Chemistry:Aquilanti–Mundim deformed Arrhenius model

From HandWiki
Short description: Chemical kinetics model

In chemical kinetics, the Aquilanti–Mundim deformed Arrhenius model is a generalization of the standard Arrhenius law.

Overview

Arrhenius plots, which are used to represent the effects of temperature on the rates of chemical and biophysical processes and on various transport phenomena in materials science, may exhibit deviations from linearity. Account of curvature is provided here by a formula, which involves a deformation of the exponential function, of the kind recently encountered in treatments of non-extensivity in statistical mechanics.

Theoretical model

Svante Arrhenius (1889) equation is often used to characterize the effect of temperature on the rates of chemical reactions.[1] The Arrhenius formula gave a simple and powerful law, which in a vast generality of cases describes the dependence on absolute temperature [math]\displaystyle{ T }[/math] of the rate constant as following,

[math]\displaystyle{ k(T)=Ae^{-E_{o}/RT} \qquad \qquad \qquad }[/math] (1)

where [math]\displaystyle{ T }[/math] is the absolute temperature, [math]\displaystyle{ R }[/math] is the gas constant and the factor [math]\displaystyle{ A }[/math] varies only slightly with temperature. The meaning attached to the energy of activation [math]\displaystyle{ E_o }[/math] is as the minimum energy, which molecules need have to overcome the threshold to reaction. Therefore, the year 1889 can be considered as the birth date of reactive dynamics as the study of the motion of atoms and molecules in a reactive event. Eq. (1) was motivated by the 1884 discovery by van't Hoff [2] of the exponential dependence from the temperature of the equilibrium constants for most reactions: Eq.(1), when used for both a reaction and its inverse, agrees with van't Hoff's equation interpreting chemical equilibrium as dynamical at the microscopic level. In case of a single rate-limited thermally activated process, an Arrhenius plot gives a straight line, from which the activation energy and the pre-exponential factor can both be determined.

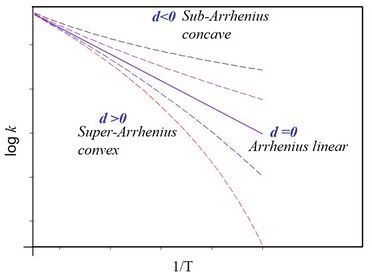
However, advances in experimental and theoretical methods have revealed the existence of deviation from Arrhenius behavior (Fig.1).

Fig.1 Arrhenius plot as a function of [math]\displaystyle{ d }[/math] parameter. The Arrhenius plot concavity is depending on the value of the [math]\displaystyle{ d }[/math] parameter.

To overcome this problem, Aquilanti and Mundim[3] proposed (2010) a generalized Arrhenius law based on algebraic deformation of the usual exponential function. Starting from the Euler[4] exponential definition given by, 

[math]\displaystyle{ e^{x}= \lim_{n \to +\infty}(1+\frac{x}{n})^{n} \qquad \qquad \qquad \qquad \qquad  }[/math]                (2)

defining the deformed exponential function as, 

[math]\displaystyle{ e^{x}_{d}\equiv\left ( 1+dx \right )^{1/d} \qquad \qquad \qquad  }[/math]                             (3)

Identifying the deformation parameter [math]\displaystyle{ d }[/math] as a continuous generalization of [math]\displaystyle{ \frac{1}{n} }[/math] . At the limit [math]\displaystyle{ d\rightarrow 0 }[/math] the d-exponential function, [math]\displaystyle{ e^{x}_{d} }[/math], coincides with the usual exponential according to the well-known limit due to Euler, that is, 

[math]\displaystyle{ \lim_{d \to 0}{e^{x}_{d}}=e^{x}   \qquad \qquad \qquad  }[/math]                                  (4)

This definition was first used in thermodynamics and statistical mechanics by Landau.[5] In the most recent scientific literature, there is a variety of deformed algebras with applications in different areas of science.[6][7] Considering the d-exponential function, we introduce the deformed reaction rate coefficient, [math]\displaystyle{ k_{d}(T) }[/math], in the following way, 

  [math]\displaystyle{ k_{d}(T)=Ae^{-\frac{E_o}{RT}}_{d}=A\left ( 1-d\frac{E_o}{RT} \right )^{1/d} }[/math]                     (5)
Fig.1a Aquilanti-Mundim plot as a function of [math]\displaystyle{ d }[/math] parameter. At the limit [math]\displaystyle{ d\rightarrow 0 }[/math] the usual Arrhenius Plot is recovered. At [math]\displaystyle{ d=0 }[/math] is Usual Arrhenius, [math]\displaystyle{ d\lt 0 }[/math] is concave and at [math]\displaystyle{ d\gt 0 }[/math] convex plot.

and at the limit [math]\displaystyle{ d\rightarrow 0 }[/math] the usual Arrhenius reaction law is recovered (Figs.1 and 1a). [math]\displaystyle{ A }[/math] is pre-exponential factor. Taking the logarithm of [math]\displaystyle{ k_{d}(T) }[/math], Eq.(5), we obtain the following expression for the non-Arrhenius plot, 

[math]\displaystyle{ \ln k_{d}(T)=\ln{A}+\frac{1}{d}\ln \left ( 1-d\frac{E_o}{RT} \right ) }[/math]                      (6)

The logarithm of the reaction rate coefficient against reciprocal temperature shows a curvature, rather than the straight-line behavior described by the usual Arrhenius law (Figs.1 and 1a).

In Tolman’s[8] definition the barrier or activation energy is a phenomenological quantity defined in terms of the slope of an Arrhenius law; it is usually assumed to be independent of absolute temperature (T), requires only local equilibrium and in general is given by 

[math]\displaystyle{ E_{o}=-\frac{\partial ln k(T) }{\partial (\frac{1}{RT}) } }[/math]                                     (7)

where [math]\displaystyle{ E_{o} }[/math] is constant and [math]\displaystyle{ R }[/math] is the ideal gas constant. To generalize Tolman´s definition, in the case chemical reactions, we assume that the barrier or activation energy is a function of the temperature given by the following differential equation, 

[math]\displaystyle{ E_{a}=-\frac{\partial ln k_{d}(T) }{\partial (\frac{1}{RT}) }=E_{o}\left ( 1-d\frac{E_o}{RT} \right )^{-1}  \qquad \qquad \qquad }[/math] or [math]\displaystyle{ \frac{1}{E_a}=\frac{1}{E_0}-\frac{d}{RT} }[/math]  →  [math]\displaystyle{ \gamma(T) = \gamma_o - d \beta }[/math]   (8)

where [math]\displaystyle{ E_{a}=E_{o} }[/math] (constant) at limit [math]\displaystyle{ d\rightarrow 0 }[/math] and the usual activation energy law is recovered as a constant. Noticeably, on the contrary of the usual Arrhenius case, the barrier or activation energy is temperature dependent and [math]\displaystyle{ k_{d}(T) }[/math] has different concavities depending on the value of the d parameter (see Figs.1 and 1a). Thus, a positive convexity means that [math]\displaystyle{ E_{a} }[/math] decreases with increasing temperature. This general result is explained by a new Tolman-like interpretation of the activation energy through Eq.(8).

In the recent literature, it is possible to find different applications to verify the applicability of this new chemical reaction formalism[9] [10] [11] [12] [13] [14] [15] [16] [17] [18]

Fig.2 – Reaction rate coefficient and activation energy equations, in both theories.

Apparent Reciprocal Activation Energy or Transitivity

[math]\displaystyle{ E_{a} }[/math] can be considered as temperature dependent. It was postulated as the basic expansion the reciprocal-activation reciprocal-temperature relationship, for which can provide a formal mathematical justification by Tolman Theorem. The [math]\displaystyle{ E_{a}(T) }[/math] function when written as the logarithmic derivative of the rate constants with respect to [math]\displaystyle{ \beta=\frac{1}{RT} }[/math], Eq. (7), the concept to an activation energy represents an energetic obstacle to the progress of the reaction: therefore its reciprocal can be interpreted as a measure of the propensity for the reaction to proceed and defined as the specific transitivity ([math]\displaystyle{ \gamma }[/math]) of the process: 

[math]\displaystyle{ \gamma(\beta)=\frac{1}{E_a(T)} }[/math]     (9)

This notation emphasizes the fact that in general the transitivity can take a gamma of values, but not including abrupt changes e.g. in the mechanism or in the phases of reactants. If it is admit a Laurent expansion in a neighbourhood around a reference value, it is possible recover the Eqs. (6) and (8).[19]

What it is call the sub-Arrhenius behaviour would be accounted for traditionally by introducing a tunnelling parameter ([math]\displaystyle{ \kappa }[/math]) in the conventional Transition-State-Theory. In the [math]\displaystyle{ d }[/math]-TST formulation, it is replace the factor [math]\displaystyle{ \kappa.\exp(-E_o\beta) }[/math] in the TST rate constant by the deformed exponential function, Eq. (3), yielding:[18] 

[math]\displaystyle{ k_{d-TST}=\frac{k_BT}{h}\frac{Q^\ddagger}{Q_r}( 1-dE_o\beta)^{1/d} }[/math]     (10)

where [math]\displaystyle{ h }[/math] is Planck constant, [math]\displaystyle{ k_B }[/math]is Boltzmann constant and [math]\displaystyle{ Q_r }[/math] is the (translational, vibrational and rotational) partition functions of the reactants, and [math]\displaystyle{ Q^\ddagger }[/math]is the partition function of the activated complex. In Ref.,[11] the significance of the parameter [math]\displaystyle{ d }[/math] and an explicit procedure for its calculation were proposed, which it is inversely proportional to the square of the barrier height ([math]\displaystyle{ E_o }[/math])and directly proportional to the square of the frequency for crossing the barrier ([math]\displaystyle{ \nu^\ddagger }[/math]) at a saddle point in the potential energy surface: 

[math]\displaystyle{ d=-\frac{1}{3} \left ( \frac{h\nu^\ddagger}{2E_o} \right )^2 }[/math]     (11)

Fields of Applications and Related Subjects

This theory was initially developed for applications in chemical kinetics problems as above discussed, but has since been applied to a wide range of phenomena:

  • the characterization of reaction rates in Chemistry,[20]
  • Transition State Theory (TST),[21][22]
  • Astrochemical process,[23]
  • quantum tunneling,[24][25]
  • stereodynamics stereochemistry of kinetics processes, solid-state diffusive reactions,[9]
  • physical processes in supercooled liquids,[26][27]
  • carbon nanotubes composite,[28]
  • transport phenomena,[29][30]
  • anomalous diffusion,[31]
  • Brownian particles moving,[32]
  • transport dynamics in ionic conductors,[33]
  • a continuum approach for modeling gravitational effects on grain settling and shape distortion,[34]
  • collision theory,[35]
  • rate theory connecting kinetics to thermodynamics,[36][37]
  • nonextensive statistical mechanics,[38][39]
  • different fields of plasma chemical-physics,[40]
  • modelling of high-temperature dark current in multi-quantum well structures from MWIR to VLWI,[41]
  • molecular semiconductor problems,[42]
  • Metallurgy: perspectives on lubricant additive corrosion,[43]
  • Langevin stochastic dynamics,[44]
  • predicting solubility of solids in supercritical solvents,[45]
  • survey on operational perishables (food) quality control and logistics,[46][47][48]
  • activation energy’s on biodiesel reaction,[49][50][51]
  • flux over population analysis,[52]
  • molecular quantum mechanics,[53][54][55]
  • biological activity,[56]
  • drug design,[57]
  • protein folding.[58]
  • Motor proteins,[59]
  • Microbial growth laws,[60]
  • Water dynamics[61]
  • Classroom on Motivation and Sociability[62]
  • Virial coefficients in chemical reaction[63]
  • Diffusion in a binary colloidal mixture[64]
  • Claisen–Schmidt condensation[65]
  • Thermotherapy[66]
  • Landscape topography[67]
  • 3D-printed powder components[68]
  • Glass alloy[69]
  • Li-ion Batteries[70]

References

  1. ↑ S. Arrhenius, Z. Phys. Chem. 1889, 4, 226.
  2. ↑ J. H. van't Hoff, 1884 in his book Études de Dynamique chimique.
  3. ↑ Aquilanti, Vincenzo; Mundim, Kleber Carlos; Elango, Munusamy; Kleijn, Steven; Kasai, Toshio (2010). "Temperature dependence of chemical and biophysical rate processes: Phenomenological approach to deviations from Arrhenius law". Chemical Physics Letters (Elsevier BV) 498 (1–3): 209–213. doi:10.1016/j.cplett.2010.08.035. ISSN 0009-2614. Bibcode: 2010CPL...498..209A. 
  4. ↑ L. Euler, Introductio in analysin infinitorum, Lugduni: Apud Bernuset, Delamolliere, Falque & soc., Editio nova., 1797.
  5. ↑ E. M. Landau, L. D.; Lifshitz, Statistal Physics, Elsevier Butterworth-Heinemann, 1951.
  6. ↑ Borges, Ernesto P. (2004). "A possible deformed algebra and calculus inspired in nonextensive thermostatistics". Physica A: Statistical Mechanics and Its Applications 340 (1–3): 95–101. doi:10.1016/j.physa.2004.03.082. ISSN 0378-4371. Bibcode: 2004PhyA..340...95B. 
  7. ↑ Tsallis, Constantino (1988). "Possible generalization of Boltzmann-Gibbs statistics". Journal of Statistical Physics (Springer Science and Business Media LLC) 52 (1–2): 479–487. doi:10.1007/bf01016429. ISSN 0022-4715. Bibcode: 1988JSP....52..479T. 
  8. ↑ Tolman, Richard C. (1920). "Statistical Merchanics Applied to Chemical Kinetics". Journal of the American Chemical Society (American Chemical Society (ACS)) 42 (12): 2506–2528. doi:10.1021/ja01457a008. ISSN 0002-7863. 
  9. ↑ 9.0 9.1 Luiggi Agreda, Ney J. (2016-07-06). "Aquilanti–Mundim deformed Arrhenius model in solid-state reactions". Journal of Thermal Analysis and Calorimetry (Springer Nature) 126 (3): 1175–1184. doi:10.1007/s10973-016-5566-8. ISSN 1388-6150. 
  10. ↑ Rampino, Sergio; Suleimanov, Yury V. (2016-12-09). "Thermal Rate Coefficients for the Astrochemical Process C + CH+ → C2+ + H by Ring Polymer Molecular Dynamics". The Journal of Physical Chemistry A (American Chemical Society (ACS)) 120 (50): 9887–9893. doi:10.1021/acs.jpca.6b10592. ISSN 1089-5639. PMID 27934333. Bibcode: 2016JPCA..120.9887R. 
  11. ↑ 11.0 11.1 Silva, Valter H.C.; Aquilanti, Vincenzo; de Oliveira, Heibbe C.B.; Mundim, Kleber C. (2013). "Uniform description of non-Arrhenius temperature dependence of reaction rates, and a heuristic criterion for quantum tunneling vs classical non-extensive distribution". Chemical Physics Letters (Elsevier BV) 590: 201–207. doi:10.1016/j.cplett.2013.10.051. ISSN 0009-2614. Bibcode: 2013CPL...590..201S. 
  12. ↑ Cavalli, S.; Aquilanti, V.; Mundim, K. C.; De Fazio, D. (2014-06-13). "Theoretical Reaction Kinetics Astride the Transition between Moderate and Deep Tunneling Regimes: The F + HD Case". The Journal of Physical Chemistry A (American Chemical Society (ACS)) 118 (33): 6632–6641. doi:10.1021/jp503463w. ISSN 1089-5639. PMID 24893210. Bibcode: 2014JPCA..118.6632C. 
  13. ↑ Coutinho, Nayara D.; Silva, Valter H. C.; de Oliveira, Heibbe C. B.; Camargo, Ademir J.; Mundim, Kleber C.; Aquilanti, Vincenzo (2015-04-13). "Stereodynamical Origin of Anti-Arrhenius Kinetics: Negative Activation Energy and Roaming for a Four-Atom Reaction". The Journal of Physical Chemistry Letters (American Chemical Society (ACS)) 6 (9): 1553–1558. doi:10.1021/acs.jpclett.5b00384. ISSN 1948-7185. PMID 26263312. 
  14. ↑ Coutinho, Nayara D.; Aquilanti, Vincenzo; Silva, Valter H. C.; Camargo, Ademir J.; Mundim, Kleber C.; de Oliveira, Heibbe C. B. (2016-05-26). "Stereodirectional Origin of anti-Arrhenius Kinetics for a Tetraatomic Hydrogen Exchange Reaction: Born–Oppenheimer Molecular Dynamics for OH + HBr". The Journal of Physical Chemistry A (American Chemical Society (ACS)) 120 (27): 5408–5417. doi:10.1021/acs.jpca.6b03958. ISSN 1089-5639. PMID 27205872. Bibcode: 2016JPCA..120.5408C. 
  15. ↑ Aquilanti, V.; Mundim, K.C.; Cavalli, S.; De Fazio, D.; Aguilar, A.; Lucas, J.M. (2012). "Exact activation energies and phenomenological description of quantum tunneling for model potential energy surfaces. The F+H2 reaction at low temperature". Chemical Physics (Elsevier BV) 398: 186–191. doi:10.1016/j.chemphys.2011.05.016. ISSN 0301-0104. Bibcode: 2012CP....398..186A. 
  16. ↑ K. C. Mundim and M. S. P. Mundim, Rev. Proc. Químicos. 2013, 14, 21.
  17. ↑ V. H. C. Silva, H. C. B. Oliveira and K. C. Mundim, Rev. Proc. Químicos. 2013, 14, 9.
  18. ↑ 18.0 18.1 Carvalho-Silva, Valter H.; Aquilanti, Vincenzo; de Oliveira, Heibbe C. B.; Mundim, Kleber C. (2016-11-17). "Deformed transition-state theory: Deviation from Arrhenius behavior and application to bimolecular hydrogen transfer reaction rates in the tunneling regime". Journal of Computational Chemistry (Wiley) 38 (3): 178–188. doi:10.1002/jcc.24529. ISSN 0192-8651. PMID 27859380. 
  19. ↑ Aquilanti, Vincenzo; Coutinho, Nayara Dantas; Carvalho-Silva, Valter Henrique (2017-04-28). "Kinetics of low-temperature transitions and a reaction rate theory from non-equilibrium distributions" (in en). Phil. Trans. R. Soc. A 375 (2092): 20160201. doi:10.1098/rsta.2016.0201. ISSN 1364-503X. PMID 28320904. Bibcode: 2017RSPTA.37560201A. 
  20. ↑ Firaha, Dzmitry S.; Döntgen, Malte; Berkels, Benjamin; Leonhard, Kai (2018-07-24). "Pressure-Dependent Rate Constant Predictions Utilizing the Inverse Laplace Transform: A Victim of Deficient Input Data". ACS Omega 3 (7): 8212–8219. doi:10.1021/acsomega.8b00311. ISSN 2470-1343. PMID 31458958. 
  21. ↑ Carvalho-Silva, Valter H.; Aquilanti, Vincenzo; de Oliveira, Heibbe C. B.; Mundim, Kleber C. (2016-11-17). "Deformed transition-state theory: Deviation from Arrhenius behavior and application to bimolecular hydrogen transfer reaction rates in the tunneling regime". Journal of Computational Chemistry 38 (3): 178–188. doi:10.1002/jcc.24529. ISSN 0192-8651. PMID 27859380. 
  22. ↑ Yin, Cangtao; Zhou, Yanjun; Du, Jiulin (November 2014). "The power-law TST reaction rate coefficient with tunneling correction". Physica A: Statistical Mechanics and Its Applications 413: 294–300. doi:10.1016/j.physa.2014.06.051. ISSN 0378-4371. Bibcode: 2014PhyA..413..294Y. 
  23. ↑ Rampino, Sergio; Suleimanov, Yury V. (2016-12-09). "Thermal Rate Coefficients for the Astrochemical Process C + CH+ → C2+ + H by Ring Polymer Molecular Dynamics". The Journal of Physical Chemistry A 120 (50): 9887–9893. doi:10.1021/acs.jpca.6b10592. ISSN 1089-5639. PMID 27934333. Bibcode: 2016JPCA..120.9887R. 
  24. ↑ Heskel, Mary A.; O’Sullivan, Odhran S.; Reich, Peter B.; Tjoelker, Mark G.; Weerasinghe, Lasantha K.; Penillard, Aurore; Egerton, John J. G.; Creek, Danielle et al. (2016-03-21). "Convergence in the temperature response of leaf respiration across biomes and plant functional types". Proceedings of the National Academy of Sciences 113 (14): 3832–3837. doi:10.1073/pnas.1520282113. ISSN 0027-8424. PMID 27001849. Bibcode: 2016PNAS..113.3832H. 
  25. ↑ Silva, Valter H.C.; Aquilanti, Vincenzo; de Oliveira, Heibbe C.B.; Mundim, Kleber C. (December 2013). "Uniform description of non-Arrhenius temperature dependence of reaction rates, and a heuristic criterion for quantum tunneling vs classical non-extensive distribution". Chemical Physics Letters 590: 201–207. doi:10.1016/j.cplett.2013.10.051. ISSN 0009-2614. Bibcode: 2013CPL...590..201S. 
  26. ↑ Rosa, A.C.P.; Vaveliuk, Pablo; Mundim, Kleber C.; Moret, M.A. (May 2016). "A model for diffusive systems: Beyond the Arrhenius mechanism". Physica A: Statistical Mechanics and Its Applications 450: 317–322. doi:10.1016/j.physa.2015.12.122. ISSN 0378-4371. Bibcode: 2016PhyA..450..317R. 
  27. ↑ Rosa Junior, A. C. P.; Cruz, C.; Santana, W. S.; Moret, M. A. (2019-08-27). "Characterization of the non-Arrhenius behavior of supercooled liquids by modeling nonadditive stochastic systems". Physical Review E 100 (2): 022139. doi:10.1103/physreve.100.022139. ISSN 2470-0045. PMID 31574742. Bibcode: 2019PhRvE.100b2139R. 
  28. ↑ Chen, Biao; Kondoh, Katsuyoshi (2016-09-06). "Sintering Behaviors of Carbon Nanotubes—Aluminum Composite Powders". Metals 6 (9): 213. doi:10.3390/met6090213. ISSN 2075-4701. 
  29. ↑ Machado, Hugo G.; Sanches-Neto, Flávio O.; Coutinho, Nayara D.; Mundim, Kleber C.; Palazzetti, Federico; Carvalho-Silva, Valter H. (2019-09-25). ""Transitivity": A Code for Computing Kinetic and Related Parameters in Chemical Transformations and Transport Phenomena". Molecules 24 (19): 3478. doi:10.3390/molecules24193478. ISSN 1420-3049. PMID 31557893. 
  30. ↑ Chaudhury, Manoj K.; Goohpattader, Partho Sarathi (February 2013). "Activated drops: Self-excited oscillation, critical speeding and noisy transport". The European Physical Journal E 36 (2): 15. doi:10.1140/epje/i2013-13015-2. ISSN 1292-8941. PMID 23412834. 
  31. ↑ Guo, Ran; Du, Jiulin (August 2015). "The precise time-dependent solution of the Fokker–Planck equation with anomalous diffusion". Annals of Physics 359: 187–197. doi:10.1016/j.aop.2015.04.019. ISSN 0003-4916. Bibcode: 2015arXiv150406382G. 
  32. ↑ Zhou, Yanjun; Yin, Cangtao (2016-06-30). "Time-dependent Kramers escape rate in overdamped system with power-law distribution". International Journal of Modern Physics B 30 (17): 1650095. doi:10.1142/s0217979216500958. ISSN 0217-9792. Bibcode: 2016IJMPB..3050095Z. 
  33. ↑ Palchucan, C.A.; Lara, D. Peña; Correa, H. (July 2019). "A unified equation for modeling the dependency of conductivity with temperature in ionic systems". Physica A: Statistical Mechanics and Its Applications 525: 635–641. doi:10.1016/j.physa.2019.03.052. ISSN 0378-4371. Bibcode: 2019PhyA..525..635P. 
  34. ↑ Alvarado-Contreras, José A.; Olevsky, Eugene A.; Maximenko, Andrey L.; German, Randall M. (February 2014). "A continuum approach for modeling gravitational effects on grain settling and shape distortion during liquid phase sintering of tungsten heavy alloys". Acta Materialia 65: 176–184. doi:10.1016/j.actamat.2013.10.059. ISSN 1359-6454. Bibcode: 2014AcMat..65..176A. 
  35. ↑ Yin, Cangtao; Du, Jiulin (August 2014). "The collision theory reaction rate coefficient for power-law distributions". Physica A: Statistical Mechanics and Its Applications 407: 119–127. doi:10.1016/j.physa.2014.03.057. ISSN 0378-4371. Bibcode: 2014PhyA..407..119Y. 
  36. ↑ Michel, Denis (August 2018). "A probabilistic rate theory connecting kinetics to thermodynamics". Physica A: Statistical Mechanics and Its Applications 503: 26–44. doi:10.1016/j.physa.2018.02.188. ISSN 0378-4371. Bibcode: 2018PhyA..503...26M. https://hal.archives-ouvertes.fr/hal-01569569/file/thermoDM.pdf. 
  37. ↑ Aquilanti, Vincenzo; Borges, Ernesto P.; Coutinho, Nayara D.; Mundim, Kleber C.; Carvalho-Silva, Valter H. (2018-10-25). "From statistical thermodynamics to molecular kinetics: the change, the chance and the choice". Rendiconti Lincei. Scienze Fisiche e Naturali 29 (4): 787–802. doi:10.1007/s12210-018-0749-9. ISSN 2037-4631. Bibcode: 2018RLSFN..29..787A. 
  38. ↑ Guo, Ran; Du, Jiulin (November 2014). "The adiabatic static linear response function in nonextensive statistical mechanics". Physica A: Statistical Mechanics and Its Applications 414: 414–420. doi:10.1016/j.physa.2014.07.057. ISSN 0378-4371. Bibcode: 2014PhyA..414..414G. 
  39. ↑ Betzler, A. S.; Borges, E. P. (March 2012). "Nonextensive distributions of asteroid rotation periods and diameters". Astronomy & Astrophysics 539: A158. doi:10.1051/0004-6361/201117767. ISSN 0004-6361. Bibcode: 2012A&A...539A.158B. 
  40. ↑ Capitelli, Mario; Pietanza, Lucia Daniela (2019-02-07). "Past and present aspects of Italian plasma chemistry". Rendiconti Lincei. Scienze Fisiche e Naturali 30 (1): 31–48. doi:10.1007/s12210-019-00781-0. ISSN 2037-4631. Bibcode: 2019RLSFN..30...31C. 
  41. ↑ de Moura Pedroso, Diogo; Vieira, Gustavo Soares; Passaro, Angelo (February 2017). "Modelling of high-temperature dark current in multi-quantum well structures from MWIR to VLWIR". Physica E: Low-dimensional Systems and Nanostructures 86: 190–197. doi:10.1016/j.physe.2016.10.021. ISSN 1386-9477. Bibcode: 2017PhyE...86..190D. 
  42. ↑ Ando, Masahiko; Yoneya, Makoto; Kehoe, Thomas B.; Ishii, Hiroyuki; Minakata, Takashi; Kawasaki, Masahiro; Duffy, Claudia M.; Phillips, Richard et al. (2019-02-19). "Disorder and localization dynamics in polymorphs of the molecular semiconductor pentacene probed by in situ micro-Raman spectroscopy and molecular dynamics simulations". Physical Review Materials 3 (2): 025601. doi:10.1103/physrevmaterials.3.025601. ISSN 2475-9953. Bibcode: 2019PhRvM...3b5601A. https://www.repository.cam.ac.uk/handle/1810/303328. 
  43. ↑ Hunt, Gregory (2018-04-03). "New Perspectives on Lubricant Additive Corrosion: Comparison of Methods and Metallurgy". SAE Technical Paper Series. 1. pp. 2018–01–0656. doi:10.4271/2018-01-0656. https://www.sae.org/content/2018-01-0656/. 
  44. ↑ Du, Jiu-Lin (2012-02-03). "Power-law distributions and fluctuation-dissipation relation in the stochastic dynamics of two-variable Langevin equations". Journal of Statistical Mechanics: Theory and Experiment 2012 (2): P02006. doi:10.1088/1742-5468/2012/02/p02006. ISSN 1742-5468. Bibcode: 2012JSMTE..02..006D. 
  45. ↑ Tabernero, A.; Vieira de Melo, S.A.B.; Mammucari, R.; Martín del Valle, E.M.; Foster, N.R. (September 2014). "Modelling solubility of solid active principle ingredients in sc-CO2 with and without cosolvents: A comparative assessment of semiempirical models based on Chrastil's equation and its modifications". The Journal of Supercritical Fluids 93: 91–102. doi:10.1016/j.supflu.2013.11.017. ISSN 0896-8446. 
  46. ↑ Coutinho, Nayara D.; Silva, Valter H. C.; Mundim, Kleber C.; de Oliveira, Heibbe C. B. (2015-04-04). "Description of the effect of temperature on food systems using the deformed Arrhenius rate law: deviations from linearity in logarithmic plots vs. inverse temperature". Rendiconti Lincei 26 (2): 141–149. doi:10.1007/s12210-015-0407-4. ISSN 2037-4631. 
  47. ↑ Lin, Xiao; Negenborn, Rudy R.; Lodewijks, Gabriel (2015), Survey on Operational Perishables Quality Control and Logistics, Lecture Notes in Computer Science, Springer International Publishing, pp. 398–421, doi:10.1007/978-3-319-24264-4_28, ISBN 978-3-319-24263-7 
  48. ↑ Conner, J.M.; Piggott, J.R.; Paterson, A.; Withers, S. (1996), "Interactions Between Wood and Distillate Components in Matured Scotch Whisky", Flavour Science, Elsevier, pp. 419–424, doi:10.1533/9781845698232.7.419, ISBN 978-1-85573-779-2 
  49. ↑ Chendynski, Letícia Thaís; Signori Romagnoli, Érica; da Silva, Paulo Rogério Catarini; Borsato, Dionisio (2017-08-30). "Activation Energy's Deviations of the Oxidation Reaction of Biodiesel in Mixtures with Ferric Ions and Natural Antioxidant". Energy & Fuels 31 (9): 9613–9618. doi:10.1021/acs.energyfuels.7b01911. ISSN 0887-0624. 
  50. ↑ Gregório, Ana Paula H.; Borsato, Dionísio; Moreira, Ivanira; Silva, Elisângela T.; Romagnoli, Érica S.; Spacino, Kelly R. (2017-06-02). "Apparent activation energy and relative protection factor of natural antioxidants in mixture with biodiesel". Biofuels 10 (5): 607–614. doi:10.1080/17597269.2017.1332297. ISSN 1759-7269. 
  51. ↑ Romagnoli, Érica Signori; Borsato, Dionísio; Silva, Lívia Ramazzoti Chanan; Chendynski, Letícia Thais; Angilelli, Karina Gomes; Canesin, Edmilson Antônio (December 2018). "Kinetic parameters of the oxidation reaction of commercial biodiesel with natural antioxidant additives". Industrial Crops and Products 125: 59–64. doi:10.1016/j.indcrop.2018.08.077. ISSN 0926-6690. 
  52. ↑ Zhou, Yanjun; Du, Jiulin (June 2014). "Escape rate for the power-law distribution in low-to-intermediate damping". Physica A: Statistical Mechanics and Its Applications 403: 244–251. doi:10.1016/j.physa.2014.02.022. ISSN 0378-4371. Bibcode: 2014PhyA..403..244Z. 
  53. ↑ Rangel, Fernando C.; Mamiya, Arthur A.; de Oliveira, Heibbe C. B.; Vieira, Fernando M. C.; Mundim, Kleber C. (2013-07-17). "Alternative Approach to Calculate Two-Center Overlap Matrix through Deformed Exponential Function". The Journal of Physical Chemistry A 117 (30): 6622–6628. doi:10.1021/jp401631a. ISSN 1089-5639. PMID 23815463. Bibcode: 2013JPCA..117.6622R. 
  54. ↑ Rangel, Fernando C.; de Oliveira, Heibbe C.B.; Montel, Adão L.B.; Mundim, Kleber C. (November 2010). "Calculation of DFT molecular properties using the -Integral method". Physica A: Statistical Mechanics and Its Applications 389 (22): 5208–5215. doi:10.1016/j.physa.2010.06.030. ISSN 0378-4371. Bibcode: 2010PhyA..389.5208R. 
  55. ↑ de Oliveira, H. C. B.; Rangel, F. C.; Esteves, C. S.; Vieira, F. M. C.; Mundim, K. C. (2009-12-31). "Calculation of MP2and Coupled-Cluster Molecular Properties Using the q-Integral Method†". The Journal of Physical Chemistry A 113 (52): 14691–14698. doi:10.1021/jp904807b. ISSN 1089-5639. PMID 20028167. Bibcode: 2009JPCA..11314691D. 
  56. ↑ Vieira, Ernanni D.; Basso, Luis G.M.; Costa-Filho, Antonio J. (June 2017). "Non-linear van't Hoff behavior in pulmonary surfactant model membranes". Biochimica et Biophysica Acta (BBA) - Biomembranes 1859 (6): 1133–1143. doi:10.1016/j.bbamem.2017.03.011. ISSN 0005-2736. PMID 28336314. 
  57. ↑ Mandal, Arabinda; Das, Ranendu Sekhar; Singh, Bula; Banerjee, Rupendranath; Mukhopadhyay, Subrata (2017-03-21). "Penicillamine and captopril: mechanistic exploration of defensive actions of thiol drugs against a metal bound-superoxo complex". Journal of Coordination Chemistry 70 (10): 1723–1738. doi:10.1080/00958972.2017.1303488. ISSN 0095-8972. 
  58. ↑ Sarkar, Daipayan; Kang, Peiyuan; Nielsen, Steven O.; Qin, Zhenpeng (2019-07-03). "Non-Arrhenius Reaction-Diffusion Kinetics for Protein Inactivation over a Large Temperature Range". ACS Nano 13 (8): 8669–8679. doi:10.1021/acsnano.9b00068. ISSN 1936-0851. PMID 31268674. 
  59. ↑ Yadav, Saumya; Kunwar, Ambarish (2021-02-26). "Temperature-Dependent Activity of Motor Proteins: Energetics and Their Implications for Collective Behavior". Frontiers in Cell and Developmental Biology 9: 610899. doi:10.3389/fcell.2021.610899. ISSN 2296-634X. PMID 33732692. 
  60. ↑ Mairet, Francis; Gouzé, Jean-Luc; de Jong, Hidde (December 2021). "Optimal proteome allocation and the temperature dependence of microbial growth laws" (in en). npj Systems Biology and Applications 7 (1): 14. doi:10.1038/s41540-021-00172-y. ISSN 2056-7189. PMID 33686098. 
  61. ↑ Yang, Hsiao-Ching; Ge, Yung-Chi; Su, Kuan-Hsuan; Chang, Chia-Cheng; Lin, King-Chuen; Aquilanti, Vincenzo; Kasai, Toshio (December 2021). "Temperature effect on water dynamics in tetramer phosphofructokinase matrix and the super-arrhenius respiration rate" (in en). Scientific Reports 11 (1): 383. doi:10.1038/s41598-020-79271-5. ISSN 2045-2322. PMID 33431895. 
  62. ↑ González-Zamar, Mariana-Daniela; Jiménez, Luis Ortiz; Ayala, Adoración Sánchez (2021-04-13). "Design and Validation of a Questionnaire on Influence of the University Classroom on Motivation and Sociability" (in en). Education Sciences 11 (4): 183. doi:10.3390/educsci11040183. ISSN 2227-7102. 
  63. ↑ Vipin, P; Sankaranarayanan, R (September 2021). "Role of virial coefficients in chemical reaction" (in en). Pramana 95 (3): 144. doi:10.1007/s12043-021-02185-y. ISSN 0304-4289. Bibcode: 2021Prama..95..144V. https://link.springer.com/10.1007/s12043-021-02185-y. 
  64. ↑ Singh, Jalim; Mustakim, Mahammad; Anil Kumar, A V (2021-01-14). "Super-Arrhenius diffusion in a binary colloidal mixture at low volume fraction: an effect of depletion interaction due to an asymmetric barrier". Journal of Physics: Condensed Matter 33 (12): 125101. doi:10.1088/1361-648x/abd428. ISSN 0953-8984. Bibcode: 2021JPCM...33l5101S. http://dx.doi.org/10.1088/1361-648x/abd428. 
  65. ↑ Coutinho, Nayara Dantas; Machado, Hugo Gontijo; Carvalho-Silva, Valter Henrique; da Silva, Wender Alves (2021). "Topography of the free energy landscape of Claisen–Schmidt condensation: solvent and temperature effects on the rate-controlling step" (in en). Physical Chemistry Chemical Physics 23 (11): 6738–6745. doi:10.1039/D0CP05659F. ISSN 1463-9076. PMID 33710206. Bibcode: 2021PCCP...23.6738C. http://xlink.rsc.org/?DOI=D0CP05659F. 
  66. ↑ Andres, Matthias; Pinnau, René (2022), Pinnau, René; Gauger, Nicolas R.; Klar, Axel, eds., "The Cattaneo Model for Laser-Induced Thermotherapy: Identification of the Blood-Perfusion Rate" (in en), Modeling, Simulation and Optimization in the Health- and Energy-Sector (Cham: Springer International Publishing) 14: pp. 25–41, doi:10.1007/978-3-030-99983-4_2, ISBN 978-3-030-99982-7, https://link.springer.com/10.1007/978-3-030-99983-4_2, retrieved 2022-09-17 
  67. ↑ Beg, Cameran; Kieffer, John (June 2022). "Fragility and the rate of change of the energy landscape topography" (in en). Journal of Non-Crystalline Solids: X 14: 100101. doi:10.1016/j.nocx.2022.100101. Bibcode: 2022JNCSX..1400101B. 
  68. ↑ Torresani, E.; German, R. M.; Huff, R.; Olevsky, E. A. (January 2022). "Influence of gravity on sintering of 3D‐printed powder components" (in en). Journal of the American Ceramic Society 105 (1): 131–146. doi:10.1111/jace.18056. ISSN 0002-7820. https://onlinelibrary.wiley.com/doi/10.1111/jace.18056. 
  69. ↑ Emran, Khadijah M.; Omar, Inam M. A.; Arab, Sanaa T.; Ouerfelli, Noureddine (December 2022). "On the pseudo-hyperbolic behavior of charge transfer resistance–temperature dependence in corrosion behavior of Nickel based glass alloy" (in en). Scientific Reports 12 (1): 6432. doi:10.1038/s41598-022-10462-y. ISSN 2045-2322. PMID 35440686. Bibcode: 2022NatSR..12.6432E. 
  70. ↑ Allagui, Anis; Benaoum, Hachemi; Wang, Chunlei (2022-02-17). "Deformed Butler–Volmer Models for Convex Semilogarithmic Current-Overpotential Profiles of Li-ion Batteries" (in en). The Journal of Physical Chemistry C 126 (6): 3029–3036. doi:10.1021/acs.jpcc.1c09620. ISSN 1932-7447. https://pubs.acs.org/doi/10.1021/acs.jpcc.1c09620. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Chemistry:Aquilanti–Mundim_deformed_Arrhenius_model&oldid=3328449"