Cissoid

Short description: Plane curve constructed from two other curves and a fixed point

  Cissoid

  Curve C₁

  Curve C₂

  Pole O

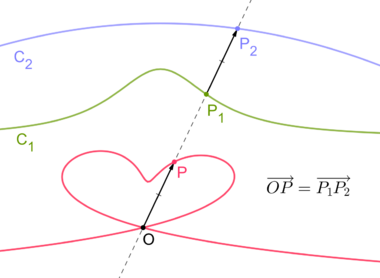
In geometry, a cissoid (from grc κισσοειδής (kissoeidēs) 'ivy-shaped') is a plane curve generated from two given curves C₁, C₂ and a point O (the pole). Let L be a variable line passing through O and intersecting C₁ at P₁ and C₂ at P₂. Let P be the point on L so that [math]\displaystyle{ \overline{OP} = \overline{P_1 P_2}. }[/math] (There are actually two such points but P is chosen so that P is in the same direction from O as P₂ is from P₁.) Then the locus of such points P is defined to be the cissoid of the curves C₁, C₂ relative to O.

Slightly different but essentially equivalent definitions are used by different authors. For example, P may be defined to be the point so that [math]\displaystyle{ \overline{OP} = \overline{OP_1} + \overline{OP_2}. }[/math] This is equivalent to the other definition if C₁ is replaced by its reflection through O. Or P may be defined as the midpoint of P₁ and P₂; this produces the curve generated by the previous curve scaled by a factor of 1/2.

Equations

If C₁ and C₂ are given in polar coordinates by [math]\displaystyle{ r=f_1(\theta) }[/math] and [math]\displaystyle{ r=f_2(\theta) }[/math] respectively, then the equation [math]\displaystyle{ r=f_2(\theta)-f_1(\theta) }[/math] describes the cissoid of C₁ and C₂ relative to the origin. However, because a point may be represented in multiple ways in polar coordinates, there may be other branches of the cissoid which have a different equation. Specifically, C₁ is also given by

[math]\displaystyle{ \begin{align} & r=-f_1(\theta+\pi) \\ & r=-f_1(\theta-\pi) \\ & r=f_1(\theta+2\pi) \\ & r=f_1(\theta-2\pi) \\ & \qquad \qquad \vdots \end{align} }[/math]

So the cissoid is actually the union of the curves given by the equations

[math]\displaystyle{ \begin{align} & r=f_2(\theta)-f_1(\theta) \\ & r=f_2(\theta)+f_1(\theta+\pi) \\ &r=f_2(\theta)+f_1(\theta-\pi) \\ & r=f_2(\theta)-f_1(\theta+2\pi) \\ & r=f_2(\theta)-f_1(\theta-2\pi) \\ & \qquad \qquad \vdots \end{align} }[/math]

It can be determined on an individual basis depending on the periods of f₁ and f₂, which of these equations can be eliminated due to duplication.

Ellipse [math]\displaystyle{ r=\frac{1}{2-\cos \theta} }[/math] in red, with its two cissoid branches in black and blue (origin)

For example, let C₁ and C₂ both be the ellipse

[math]\displaystyle{ r=\frac{1}{2-\cos \theta}. }[/math]

The first branch of the cissoid is given by

[math]\displaystyle{ r=\frac{1}{2-\cos \theta}-\frac{1}{2-\cos \theta}=0, }[/math]

which is simply the origin. The ellipse is also given by

[math]\displaystyle{ r=\frac{-1}{2+\cos \theta}, }[/math]

so a second branch of the cissoid is given by

[math]\displaystyle{ r=\frac{1}{2-\cos \theta}+\frac{1}{2+\cos \theta} }[/math]

which is an oval shaped curve.

If each C₁ and C₂ are given by the parametric equations

[math]\displaystyle{ x = f_1(p),\ y = px }[/math]

and

[math]\displaystyle{ x = f_2(p),\ y = px, }[/math]

then the cissoid relative to the origin is given by

[math]\displaystyle{ x = f_2(p)-f_1(p),\ y = px. }[/math]

Specific cases

When C₁ is a circle with center O then the cissoid is conchoid of C₂.

When C₁ and C₂ are parallel lines then the cissoid is a third line parallel to the given lines.

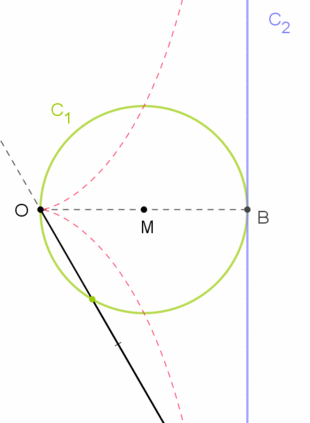
Hyperbolas

Let C₁ and C₂ be two non-parallel lines and let O be the origin. Let the polar equations of C₁ and C₂ be

[math]\displaystyle{ r=\frac{a_1}{\cos (\theta-\alpha_1)} }[/math]

and

[math]\displaystyle{ r=\frac{a_2}{\cos (\theta-\alpha_2)}. }[/math]

By rotation through angle [math]\displaystyle{ \tfrac{\alpha_1-\alpha_2}{2}, }[/math] we can assume that [math]\displaystyle{ \alpha_1 = \alpha,\ \alpha_2 = -\alpha. }[/math] Then the cissoid of C₁ and C₂ relative to the origin is given by

[math]\displaystyle{ \begin{align} r & = \frac{a_2}{\cos (\theta+\alpha)} - \frac{a_1}{\cos (\theta-\alpha)} \\ & =\frac{a_2\cos (\theta-\alpha)-a_1\cos (\theta+\alpha)}{\cos (\theta+\alpha)\cos (\theta-\alpha)} \\ & =\frac{(a_2\cos\alpha-a_1\cos\alpha)\cos\theta-(a_2\sin\alpha+a_1\sin\alpha)\sin\theta}{\cos^2\alpha\ \cos^2\theta-\sin^2\alpha\ \sin^2\theta}. \end{align} }[/math]

Combining constants gives

[math]\displaystyle{ r=\frac{b\cos\theta+c\sin\theta}{\cos^2\theta-m^2\sin^2\theta} }[/math]

which in Cartesian coordinates is

[math]\displaystyle{ x^2-m^2y^2=bx+cy. }[/math]

This is a hyperbola passing through the origin. So the cissoid of two non-parallel lines is a hyperbola containing the pole. A similar derivation show that, conversely, any hyperbola is the cissoid of two non-parallel lines relative to any point on it.

Cissoids of Zahradnik

A cissoid of Zahradnik (named after Karel Zahradnik) is defined as the cissoid of a conic section and a line relative to any point on the conic. This is a broad family of rational cubic curves containing several well-known examples. Specifically:

• The Trisectrix of Maclaurin given by

[math]\displaystyle{ 2x(x^2+y^2)=a(3x^2-y^2) }[/math]

is the cissoid of the circle [math]\displaystyle{ (x+a)^2+y^2 = a^2 }[/math] and the line [math]\displaystyle{ x=-\tfrac{a}{2} }[/math] relative to the origin.

• The right strophoid

[math]\displaystyle{ y^2(a+x) = x^2(a-x) }[/math]

is the cissoid of the circle [math]\displaystyle{ (x+a)^2+y^2 = a^2 }[/math] and the line [math]\displaystyle{ x=-a }[/math] relative to the origin.

Animation visualizing the Cissoid of Diocles

• The cissoid of Diocles

[math]\displaystyle{ x(x^2+y^2)+2ay^2=0 }[/math]

is the cissoid of the circle [math]\displaystyle{ (x+a)^2+y^2 = a^2 }[/math] and the line [math]\displaystyle{ x=-2a }[/math] relative to the origin. This is, in fact, the curve for which the family is named and some authors refer to this as simply as cissoid.

• The cissoid of the circle [math]\displaystyle{ (x+a)^2+y^2 = a^2 }[/math] and the line [math]\displaystyle{ x=ka, }[/math] where k is a parameter, is called a Conchoid of de Sluze. (These curves are not actually conchoids.) This family includes the previous examples.
• The folium of Descartes

[math]\displaystyle{ x^3+y^3=3axy }[/math]

is the cissoid of the ellipse [math]\displaystyle{ x^2-xy+y^2 = -a(x+y) }[/math] and the line [math]\displaystyle{ x+y=-a }[/math] relative to the origin. To see this, note that the line can be written

[math]\displaystyle{ x=-\frac{a}{1+p},\ y=px }[/math]

and the ellipse can be written

[math]\displaystyle{ x=-\frac{a(1+p)}{1-p+p^2},\ y=px. }[/math]

So the cissoid is given by

[math]\displaystyle{ x=-\frac{a}{1+p}+\frac{a(1+p)}{1-p+p^2} = \frac{3ap}{1+p^3},\ y=px }[/math]

which is a parametric form of the folium.

See also

• Conchoid
• Strophoid

References

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 53–56. ISBN 0-486-60288-5. https://archive.org/details/catalogofspecial00lawr/page/53. 
• C. A. Nelson "Note on rational plane cubics" Bull. Amer. Math. Soc. Volume 32, Number 1 (1926), 71-76.

External links

• Hazewinkel, Michiel, ed. (2001), "Cissoid", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/c022340 
• Weisstein, Eric W.. "Cissoid". http://mathworld.wolfram.com/Cissoid.html. 
• 2D Curves

zh:蔓叶线