Cohesion (computer science)
In computer programming, cohesion refers to the degree to which the elements inside a module belong together.[1] In one sense, it is a measure of the strength of relationship between the methods and data of a class and some unifying purpose or concept served by that class. In another sense, it is a measure of the strength of relationship between the class's methods and data themselves.
Cohesion is an ordinal type of measurement and is usually described as “high cohesion” or “low cohesion”. Modules with high cohesion tend to be preferable, because high cohesion is associated with several desirable traits of software including robustness, reliability, reusability, and understandability. In contrast, low cohesion is associated with undesirable traits such as being difficult to maintain, test, reuse, or even understand.
Cohesion is often contrasted with coupling. High cohesion often correlates with loose coupling, and vice versa.[2] The software metrics of coupling and cohesion were invented by Larry Constantine in the late 1960s as part of Structured Design, based on characteristics of “good” programming practices that reduced maintenance and modification costs. Structured Design, cohesion and coupling were published in the article Stevens, Myers & Constantine (1974)[3] and the book Yourdon & Constantine (1979);[1] the latter two subsequently became standard terms in software engineering.
High cohesion
In object-oriented programming, if the methods that serve a class tend to be similar in many aspects, then the class is said to have high cohesion.[4] In a highly cohesive system, code readability and reusability is increased, while complexity is kept manageable.
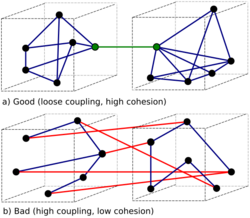
Cohesion is increased if:
- The functionalities embedded in a class, accessed through its methods, have much in common.
- Methods carry out a small number of related activities, by avoiding coarsely grained or unrelated sets of data.
- Related methods are in the same source file or otherwise grouped together; for example, in separate files but in the same sub-directory/folder.
Advantages of high cohesion (or "strong cohesion") are:
- Reduced module complexity (they are simpler, having fewer operations).
- Increased system maintainability, because logical changes in the domain affect fewer modules, and because changes in one module require fewer changes in other modules.
- Increased module reusability, because application developers will find the component they need more easily among the cohesive set of operations provided by the module.
While in principle a module can have perfect cohesion by only consisting of a single, atomic element – having a single function, for example – in practice complex tasks are not expressible by a single, simple element. Thus a single-element module has an element that either is too complicated, in order to accomplish a task, or is too narrow, and thus tightly coupled to other modules. Thus cohesion is balanced with both unit complexity and coupling.
Types of cohesion
Cohesion is a qualitative measure, meaning that the source code to be measured is examined using a rubric to determine a classification. Cohesion types, from the worst to the best, are as follows:
- Coincidental cohesion (worst)
- Coincidental cohesion is when parts of a module are grouped arbitrarily; the only relationship between the parts is that they have been grouped together (e.g., a “Utilities” class). Example:
/* Groups: The function definitions Parts: The terms on each function */ Module A { /* Implementation of r(x) = 5x + 3 There is no particular reason to group functions in this way, so the module is said to have Coincidental Cohesion. */ r(x) = a(x) + b(x) a(x) = 2x + 1 b(x) = 3x + 2 }
- Logical cohesion
- Logical cohesion is when parts of a module are grouped because they are logically categorized to do the same thing even though they are different by nature (e.g., grouping all mouse and keyboard input handling routines or bundling all models, views, and controllers in separate folders in an MVC pattern).
- Temporal cohesion
- Temporal cohesion is when parts of a module are grouped by when they are processed - the parts are processed at a particular time in program execution (e.g., a function which is called after catching an exception which closes open files, creates an error log, and notifies the user).
- Procedural cohesion
- Procedural cohesion is when parts of a module are grouped because they always follow a certain sequence of execution (e.g., a function which checks file permissions and then opens the file).
- Communicational/informational cohesion
- Communicational cohesion is when parts of a module are grouped because they operate on the same data (e.g., a module which operates on the same record of information).
- Sequential cohesion
- Sequential cohesion is when parts of a module are grouped because the output from one part is the input to another part like an assembly line (e.g., a function which reads data from a file and processes the data).
- Functional cohesion (best)
- Functional cohesion is when parts of a module are grouped because they all contribute to a single well-defined task of the module (e.g., Lexical analysis of an XML string). Example:
/* Groups: The function definitions Parts: The terms on each function */ Module A { /* Implementation of arithmetic operations This module is said to have functional cohesion because there is an intention to group simple arithmetic operations on it. */ a(x, y) = x + y b(x, y) = x * y } Module B { /* Module B: Implements r(x) = 5x + 3 This module can be said to have atomic cohesion. The whole system (with Modules A and B as parts) can also be said to have functional cohesion, because its parts both have specific separate purposes. */ r(x) = [Module A].a([Module A].b(5, x), 3) }
- Perfect cohesion (atomic)
- Example.
/* Groups: The function definitions Parts: The terms on each function */ Module A { /* Implementation of r(x) = 2x + 1 + 3x + 2 It's said to have perfect cohesion because it cannot be reduced any more than that. */ r(x) = 5x + 3 }
Although cohesion is a ranking type of scale, the ranks do not indicate a steady progression of improved cohesion. Studies by various people including Larry Constantine, Edward Yourdon, and Steve McConnell[5] indicate that the first two types of cohesion are inferior; communicational and sequential cohesion are very good; and functional cohesion is superior.
See also
- Coupling (computer science)
- List of object-oriented programming terms
- Static code analysis
References
- ↑ 1.0 1.1 Structured Design: Fundamentals of a Discipline of Computer Program and Systems Design. Yourdon Press. 1979. ISBN 978-0-13-854471-3. Bibcode: 1979sdfd.book.....Y.
- ↑ Software Architect's Handbook. Packt Publishing. 2018. pp. 175. ISBN 978-178862406-0.
- ↑ "Structured design". IBM Systems Journal 13 (2): 115–139. June 1974. doi:10.1147/sj.132.0115.
- ↑ Software Engineering. Rutgers University. 2012.
- ↑ Code Complete (2 ed.). June 2004. pp. 168-171. ISBN 978-0-7356-1967-8.
External links
 |
